Код с контролем на чётность

У него все разрешённые кодовые слова содержат чёткое число единиц. Для его формирования к обыкновенному коду достаточно добавить один избыточный (контрольный) разряд.

Если надо передать S=4 сообщения, то обыкновенный код должен иметь 2 разряда, которые несут информацию, а третий контрольный разряд определяется исходя из чётности числа единиц в слове:

Код, у которого разряды делятся на информационные (служащие для передачи сообщений) и контрольные (служащие для коррекции ошибок), называется разделимым.

При приёме кода с контролем на чётность, подсчитывается число единиц. Если оно чётно, то сообщение принимается, в противном случае – игнорируется.

Можно решить данную задачу, используя контакты поляризованных реле Л1-Л3, которые фиксируют качества импульсов тока. Данный декодер вместо восьми имеет четыре выхода (S=4), соответствующие разрешённым комбинациям. При приёме запрещённого слова ни один из выходов декодера не подключается и команда не выполняется. В этом заключается обнаружение ошибки.

Характеристики:

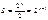- ёмкость, n – количество символов в коде;

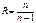- избыточность;

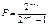- обнаруживающая способность.

Данным кодом обнаруживаются все ошибки, которые нарушают чётность числа единиц. Это все ошибки нечётной кратности (в том числе и одиночные).

Равновесный код (код с постоянным числом «1»)

У этого кода все кодовые слова имеют постоянное число единиц, поэтому его ещё называют кодом «m из n», т.к. каждое слово имеет m единиц из n разрядов. Число m называют весом кода.

Характеристики:

;

; ;

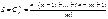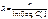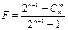Примеры : коды ’’ 2 из 5” ( ТДУ )

‘’ 2 из 4’’

‘’ 2 из 4 ‘’ ‘’ 2 из 5 ‘’

1 2 3 4 1 2 3 4 5

0 0 1 1 1 1 0 0 0

0 1 0 1 0 1 1 0 0

0 1 1 0 0 0 1 1 0

1 0 0 1 0 0 0 1 1

1 0 1 0 1 0 0 0 1

1 1 0 0 1 0 1 0 0

0 1 0 1 0

0 0 1 0 1

2 1 0 0 1 0

C = 4*3/2=6 0 1 0 0 1

4 2

C = 5*4 / 2 = 10

Равномерный код не является разделимым, т.е. его разряды нельзя разделить на информационные и контрольные.

При приеме слова, декодер подсчитывает число единиц и , если оно равно m, то сообщение принимается.

Код обнаруживает ошибки нарушающие вес ( т.е. все одиночные ошибки) , все ошибки нечетной кратности , а также некоторые ошибки четной кратности . Не обнаруживая ошибки четной кратности, у которых число искажений вида 0 Þ1 равно числу искажений1Þ 0

ПРИМЕР ДЕКОДЕРА

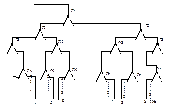
КОД С ПОВТОРЕНИЕМ

Относится к корреляционным, т.е. у него существует зависимость между определенными элементами кода.

У данного кода каждое обыкновенное слово повторяется дважды.

Например , для S=4

Простой код С повторением

1 2 1 2 3 4

0 0 0 0 0 0

0 1 0 1 0 1

1 0 1 0 1 0

1 1 1 1 1 1

123 123

инф. Контрол.

Данный относится к разделимым .Первый и второй разряды можно считать информационными , а третий и четвертый – контрольными.

Характеристики:

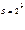
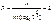
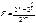
При приеме требуется сравнивать одинаковые элементы обоих частей кода и , если они совпадают, то сообщение принимается. Декодер в этом случае состоит из схем декодера обратного кода, схемы сравнения и включения управляемых объектов.

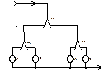
Cхема обычного декодера

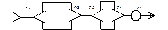
Схема сравнения

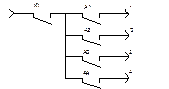
Схема включения управляющих объектов

Данным кодом не обнаруживаются только ошибки четной кратности, в которых присутствуют искожения одинаковых разрядов.