На вход цепи подадим синусоидальное напряжение
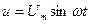
Ток в цепи с емкостью

Выразим 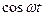 через
через 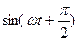 , получим
, получим
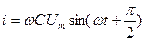
Т.е. ток опережает по фазе напряжения на 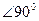 . Из выражения тока следует, что
. Из выражения тока следует, что 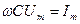 .
.
Это выражение можно написать в таком виде:
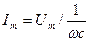 - что является выражением закона Ома для цепи с идеальной емкостью.
- что является выражением закона Ома для цепи с идеальной емкостью.
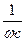 - выражает величину сопротивления, которое называется реактивным емкостным сопротивлением и обозначается ХС .
- выражает величину сопротивления, которое называется реактивным емкостным сопротивлением и обозначается ХС .

ХС - это величина, характеризующая противодействие, оказываемое напряжением на обкладках конденсатора переменному току.
В комплексной форме:
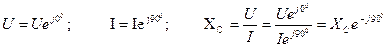
Для алгебраической формы:
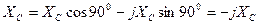
Зависимость ХС от частоты приведена на графике 4.2.4.1
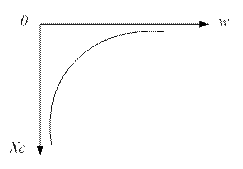
Рисунок 4.2.4.1
Векторная диаграмма цепи на рис. 4.2.4.2
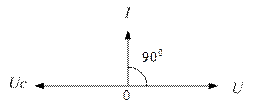
Рисунок 4.2.4.1
4.2.4. Цепь с активным сопротивлением и емкостью
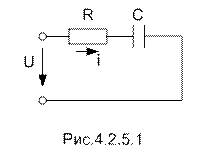
Если в цепи с последовательно соединенными R и С протекает синусоидальный ток 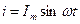 , то он создает падения напряжений на активном и емкостном сопротивлениях.
, то он создает падения напряжений на активном и емкостном сопротивлениях.

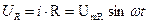
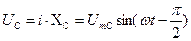
Напряжение цепи изменяется по синусоидальному закону и отстает по фазе от тока на угол 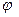 < 90°, т.е.
< 90°, т.е. 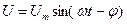
Построим векторную диаграмму (рис. 4.2.5.2) и по ней определим действующее значение напряжения.
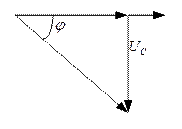
Рис. 4.2.5.2
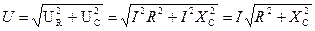
Откуда закон Ома для данной цепи:
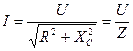
В символическом виде:
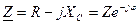
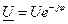 ;
; 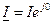 ;
; 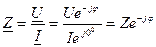
Полная мощность: 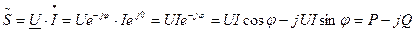
Пример:
R=8 Ом
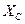 =6 Ом
=6 Ом
U=220В
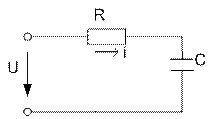
Определить: I, 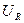 ,
, 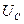 ,S
,S
Решение:
1. Полное сопротивление цепи:
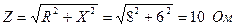
2. Ток в цепи:
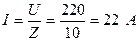
3. Напряжение на участках:
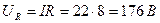
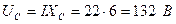
4. Полная мощность:
S=UI=220∙22=4840 ВА
Активная мощность:
Р=S cos 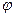 =4840∙0,8=3872 Вт
=4840∙0,8=3872 Вт
Реактивная мощность:
Q=S sin 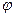 =4840∙0,6=2904 Вар
=4840∙0,6=2904 Вар
(sin 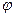 =
=  )
)
Вопросы для самоконтроля
1. Приведите векторную диаграмму напряжений для цепи RC.
2. Запишите формулу закона Ома в символическом виде для цепи RC.
3. Запишите закон изменения напряжения на емкости, если ток в цепи изменяется по закону: i= 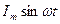 .
.
4. Рассчитайте полное сопротивление цепи в символическом виде, если R=12 Ом, С=253 мкФ, f=50 Гц.
4.2.5. Неразветвленная цепь с R,L,C
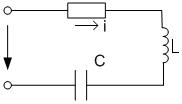
Рис. 4.2.6.1
Если в цепи, рис. 4.2.6.1 протекает синусоидальный ток, то он создает падение напряжений на всех элементах цепи. По второму закону Кирхгофа:
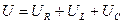
где  = i R =
= i R = 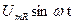
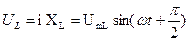
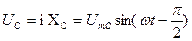
Так как, в рассматриваемой цепи имеется два реактивных сопротивления 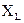 и
и 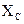 , то возможны три режима:
, то возможны три режима:
1) 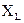 >
> 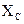 ; 2)
; 2) 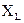 <
< 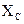 ; 3)
; 3) 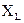 =
= 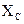
Векторная диаграмма для случая 1) изображена на рис. 4.2.6.2.
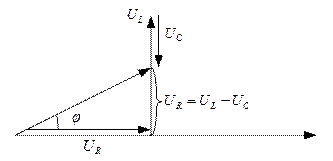
Рис. 4.2.6.2.
Знак перед углом 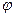 зависит от режима цепи.
зависит от режима цепи.
Если 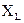 >
> 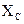 ,
, 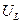 >
> 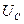 , цепь имеет индуктивный характер, угол
, цепь имеет индуктивный характер, угол 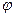 положительный.
положительный.
Если 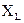 <
< 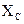 ,
, 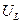 <
< 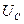 , цепь имеет емкостной характер, угол
, цепь имеет емкостной характер, угол 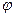 отрицательный.
отрицательный.
Закон Ома:
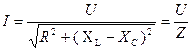
где Z = 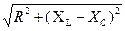 - полное сопротивление.
- полное сопротивление.
В комплексной форме: 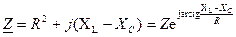
Треугольники сопротивлений и мощностей приведены на рисунке 4.2.6.3. (а и б)
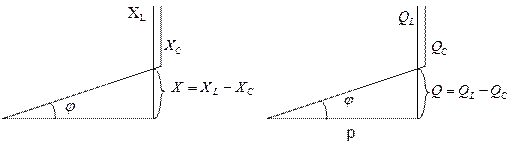
а) б)
рис. 4.2.6.3.
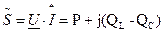 - полная мощность в комплексном виде.
- полная мощность в комплексном виде.
4.2.6. Колебательный контур
Дата добавления: 2016-11-29; просмотров: 2289;











