Системы плоских прямоугольных координат в проекции Гаусса – Крюгера

Для описания положения предметов можно использовать различные системы координат. Различные области науки и техники используют декартову систему координат. В общем случае это косоугольная система. Как частный случай - прямоугольная. В числе прямоугольных могут быть две:- правая и левая системы.

Система координат определяется координатным репером, то есть связной единичных ортов. Прямоугольная декартова система координат задается связкой трех взаимно перпендикулярных единичных векторов ортов Е₁ , Е₂ и Е₃ (рис. 1.8). Если при вращении от 1-го орта ко 2-му орту направление 3-го орта соответствует движению по правилу правого винта, то это правая система координат (рис. 1.8,а), если по правилу левого винта – это левая система координат (рис.1.8,б).

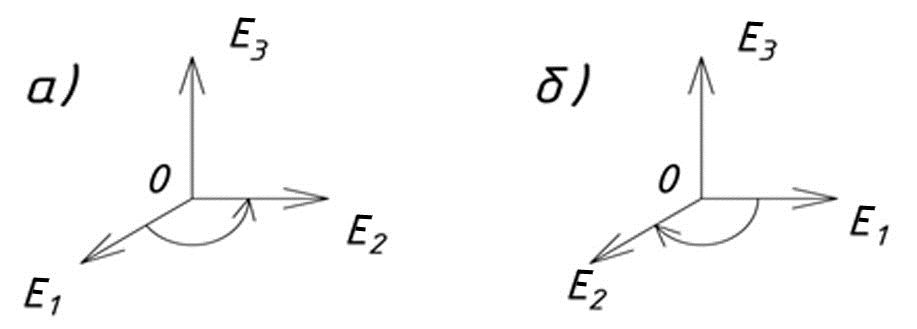Рис. 1.8. Декартовы системы координат: а-правая; б-левая

При использовании плоской системы координат предполагается, что 3-й орт направлен на наблюдателя. В геодезии, в отличие от математики и других дисциплин, принята левая система координат. В этой системе (положительное) вращение от 1-го орта ко 2-му орту происходит по ходу часовой стрелки. Так принято в соответствии с движением небесных светил и так устроены шкалы угломерных приборов.

В зависимости от выбранной системы координат можно определить положительно-ориентированный многоугольник. Так, например, в левой системе многоугольник будет положительно ориентирован, если обход вершин по его контуру будет происходить по ходу часовой стрелки. В положительно ориентированном многоугольнике внутренними углами при вершинах будут правые по ходу углы.

Развернуть поверхность сфероида на плоскость без складок и разрывов не представляется возможным. Задача несколько упростится, если развернуть (проецировать) на поверхность цилиндра часть поверхности сфероида. Пусть цилиндр плотно оборачивает поверхность сфероида таким образом, что его ось расположена перпендикулярно (поперек) к малой оси сфероида. Касание поверхностей произойдет по меридиану сфероида, который принято называть осевым. Поскольку осевой меридиан принадлежит одновременно двум поверхностям, то длины линий по меридианам на цилиндрической поверхности не искажаются.

Карл Фридрих Гаусс предложил функции отображения (проецирования) геометрических фигур с поверхности сфероида на поверхность цилиндра таким образом, что углы при вершинах в бесконечно малых геометрических фигурах на поверхности эллипсоида при проецировании на плоскость не искажаются. Такая проекция еще называется равноугольной. Искажение длин и площадей происходит по мере удаления от осевого меридиана. Площади в проекции Гаусса всегда больше, чем на поверхности эллипсоида.

Рабочие формулы для вычисления плоских прямоугольных координат по геодезическим координатам предложил в 1912 году немецкий инженер Крюгер [3].

Постановлением Совета Министров СССР от 7 апреля 1946 года № 760 на основе результатов выполненного уравнивания была введена единая система геодезических координат и высот на территории СССР – система координат 1942 года.

Геодезическим координатам 1942 года в проекции Гаусса – Крюгера соответствуют плоские прямоугольные координаты СК – 42. Система СК – 42 состоит, по существу, из 60 отдельных прямоугольных систем координат, поэтому в записи ординат обязательно должен присутствовать порядковый номер 6-градусной зоны. Отсчет абсцисс всегда происходит от экватора. Начало отсчета ординат в каждой 6-градусной зоне условно отодвигают от осевого меридиана на запад на 500 км.

Ось абсцисс в геодезии направлена вверх.

Для целей народного хозяйства во времена, когда СК – 42 была секретной, требовался координатный метод для межевания, строительства и геодезического обеспечения городов. В 60-х годах XX века была введена СК – 63 в качестве «полуоткрытой» системы координат. Эта система должна была отличаться от государственной системы координат СК – 42, поэтому были внесены изменения: ширина зоны устанавливалась произвольно, присутствовал параллельный сдвиг, разворот. Связь СК – 63 с СК – 42 являлась закрытой информацией.

С апреля 2013 года в Курской области применяется местная (региональная) система координат МСК – 46. Местная система координат получается из СК – 63 путем сдвига начала отсчёта ординат и абсцисс на некоторые константы.