Растворимость газов в жидкостях

Она зависит от давления и температуры. Растворимость газов неодинакова из-за различной химической природы.

Пример:

N₂, H₂ – мало растворимы в воде, растворимость NH₃, HCl очень велика, в одном объеме H₂O растворяется 700 объемов аммиака NH₃.

Газ + H₂O > 3,5 объема О₂ в одном объеме Н₂О экзотермический процесс. С повышением температуры растворимость некоторых газов уменьшается. При постоянной температуре и невысоком давлении растворимость газов, не вступающих в химическое взаимодействие с растворителем, подчиняется закону Генри – Дальтона, который состоит из нескольких частей.

1 часть: масса газа, растворяющаяся в данном объеме жидкости, пропорциональна давлению, которое газ производит на жидкость.

Например, CO₂ под давлением загоняем в бутылку.

2 часть: объем газа не зависит от давления.

3 часть: если смесь газов растворять, то растворимость каждой составной части пропорциональна своему парциальному давлению.

Газы, реагирующие с водой, не подчиняются закону Генри – Дальтона.

4. Растворы неэлектролитов. Закон Рауля и его следствия

Рассмотрим модель идеального раствора. Раствор называется идеальным, если в нем отсутствует взаимодействие между частицами (молекулами, атомами, ионами). Растворы неэлектролитов – частицы, плохо растворимые в воде, так как нет носителя электрического заряда. Закон Рауля справедлив только для разбавленных растворов неэлектролитов.

Пусть P_BO – давление пара над чистым растворителем, при постоянной температуре T₁; P_B– давление пара растворителя при этой же температуре, но над раствором, состоящим из нелетучего компонента А (сахар), и чистым жидким растворителем В:

P_B = f (T).

Разность P_BO – P_B равна понижению давления пара.

Величина (P_BO – P_B) /P_BO – относительное понижение упругости пара = X_A = ?P/P_BO, где X_A– мольная доля, P_BO > P_B, ?P = P_BO – P_B – абсолютное понижение упругости пара.

Закон Рауля. Относительное понижение упругости пара растворителя над раствором равно мольной доле растворенного нелетучего компонента.

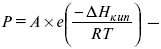
барометрическая формула Больцмана.

Следствия из закона Рауля:

1. Растворение нелетучего компонента в растворителе приводит к расширению температурной области существования жидкой фазы.

2. Понижение температуры замерзания и повышение температуры кипения прямо пропорциональны моляльной концентрации растворенного вещества.

3. Растворы, содержащие одинаковое число молей растворенных веществ в одинаковых молях растворителя, обнаруживают одно и то же понижение температуры замерзания и одно и то же повышение температуры кипения.

?t_кип=Э x С_{моляльн},

где Э – эбуллиоскопическая константа, +0,52.

?t_зам=К x С_{моляльн},

где К – криоскопическая константа, равная –1,86.

Эбуллиоскопическая константа – разница между температурой кипения раствора и температурой чистого растворителя.

Криоскопическая константа – разница между температурой замерзания раствора и температурой чистого растворителя.

Для решения задач об этих константах необходимо знать массу растворенного вещества и массу раствора. Например, масса хлороформа (трихлорметан CHCl₃) рассчитывается по формуле:

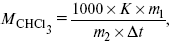
где m₁ – масса растворенного вещества;

m₂ – масса растворителя;

?t – величина, показывающая на сколько градусов понизилась температура;

К – криоскопическая константа.

Осмос

Осмос – явление селективной диффузии определенного сорта частиц через полупроницаемую перегородку. Это явление впервые описал аббат Нолле в 1748 г. Перегородки, проницаемые только для воды или другого растворителя и непроницаемые для растворенных веществ, как низкомолекулярных, так и высокомолекулярных, могут быть изготовлены из полимерных пленок (коллодия) или гелеобразных осадков, например, ферроцианида меди Cu₂[Fe(CN)₆]; этот осадок образуется в порах перегородки стеклянного фильтра при погружении пористого материала сначала в раствор медного купороса (CuSO₄ x 5H₂O), а затем желтой кровяной соли K₂[Fе(CN)₆] . Вещества диффундируют через такую перегородку, что является важным случаем осмоса, позволяющим измерять осмотическое дав-ление, т. е. осмотическое давление – мера стремления растворенного вещества перейти вследствие теплового движения в процессе диффузии из раствора в чистый растворитель; распределяется равномерно по всему объему растворителя, понизив первоначальную концентрацию раствора.

За счет осмотического давления сила заставляет жидкость подниматься вверх, это осмотическое давление уравновешивается гидростатическим давлением. Когда скорости диффундирующих веществ станут равны, тогда осмос прекратится.

Закономерности:

1. При постоянной температуре осмотическое давление раствора прямо пропорционально концентрации растворенного вещества.

2. Осмотическое давление пропорционально абсолютной температуре.

В 1886 г. Я. Г. Вант-Гофф показал, что величина осмотического давления может быть выражена через состояние газа

P_оснV = RT.

Закон Авогадро применим к разбавленным растворам: в равных объемах различных газов при одинаковой температуре и одинаковом осмотическом давлении содержится одинаковое число растворенных частиц. Растворы различных веществ, имеющие одинаковые молярные концентрации при одинаковой температуре, имеют одинаковое осмотическое давление. Такие растворы называются изотоническими.

Осмотическое давление не зависит от природы растворяемых веществ, а зависит от концентрации. Если объем заменить на концентрацию, получим:

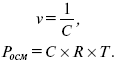
Рассмотрим закон Вант-Гоффа: осмотическое давление раствора численно равно тому давлению, которое производило бы данное количество растворенного вещества, если бы оно в виде идеального газа занимало при данной температуре объем, равный объему раствора.

Все описанные законы относятся к бесконечно разбавленным растворам.

Парциальное давление

Парциальное давление – то давление, которое оказывал бы газ, входящий в газовую смесь, если бы из нее были удалены все остальные газы при условии сохранения постоянными температуры и объема.

Общее давление газовой смеси определяется законом Дальтона: общее давление смеси газов, занимающих определенных объем, равно сумме парциальных давлений, которыми обладал бы каждый отдельно взятый газ, если бы он занимал объем, равный объему смеси газов.

Р = Р₁ + Р₂ + Р₃ + … + Р_к,

где Р – общее давление;

Р_к – парциальное давление компонентов.

Фугитивность

Фугитивность – функция, характеризующая состояние данного вещества в чистом виде или в смеси с другими веществами при заданных температуре и давлении. По-другому она называется термодинамическая летучесть; является величиной, количественно характеризующей способность вещества к выходу из данной фазы, но выражающей эту характеристику в единицах давления. Для жидкостей и твердых тел она связана с давлением насыщенного пара и становится равной ему, когда к пару применимы законы идеальных газов. Для идеального газа, чтобы найти, например, изменение энергий Гиббса при изотермическом процессе, надо просто решить задачу в соответствии с уравнением Менделеева – Клапейрона:

Для упрощения расчета Г. Льюисом в 1901 г. была введена функция f от Р –фугитивность. Заменяя давление фугитивностью, мы сохраняем простую математическую форму, которую имеют термодинамические зависимости для идеального газа.

Итак, новая функция определяется уравнением:

или

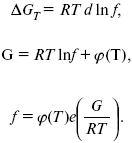
Значения фугитивности при больших давлениях (и низких температурах) сильно отличаются от Р. Так, при t = 0 и Р = 1200, f_co = 2663, при t = 0, P = 100, f_NH3 = 204, а для N₂ при t = –75, P = 6000, f – 2 x 10⁶, то есть фугитивность становится несоизмеримой с давлением.

Фугитивность можно определить как давление, которое должна производить данная реальная система, чтобы оказывать такое же действие, как и идеальная. Она характеризует отклонение от идеального состояния и, подобно давлению для идеального газа, может рассматриваться как мера рассеиваемости вещества. С приближением реального газа к идеальному состоянию/по величине приближается к Р, так что для идеального газа при всех давлениях обе величины становятся равными, то есть:

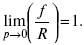
Видно, что размерность/совпадает с размерностью Р. Следует подчеркнуть, что замена Рна/в уравнениях идеального газа при переходе к реальному справедлива только для изотермического процесса, так как в соответствии с (2) фугитивность является специфической изотермической функцией. Для характеристики степени отклонения газа от идеального состояния вводят также величину

где ᵞ – коэффициент фугитивности.

Закон Генри

Фугитивность растворителя в разбавленном растворе не зависит от природы растворенного вещества и вычисляется по закону Рауля, то есть:

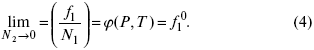
Так как фугитивность жидкости или твердого раствора равна фугитивности насыщенного пара, когда растворитель в парообразном состоянии ведет себя как идеальный газ, уравнение (4) переходит в

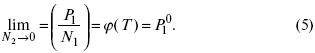
Зная зависимостьf₁ от состава, можно найти зависимость f₂ от N₂ по уравнению:

N₁dRT ln (f₁N₁) + N₂dRT ln f₂ = 0

или

откуда

ln f₂ = ln N₂ + const.

Переписывая это уравнение в виде

ln f₂ = ln N₂+ ln K(P, T),

получим при P,T= const

f₂ = KN₂

или

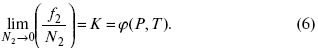
Если в последнем уравнении рассматривать f₂ как фугитивность растворенного вещества в газовой фазе, сосуществующей жидкой (твердой), то она является точной термодинамической формой закона Генри.

Его формулировка: зависимость растворимости газа в жидкости от давления, заключается в том, что при постоянной температуре газа, растворенного в данной жидкости, растворимость газа пропорциональна его давлению над раствором.

Краткая формулировка: растворимость газа пропорциональна давлению. Этот закон установлен в 1803 г. Ему отвечает уравнение:

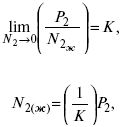
где Р₂ – парциальное давление растворенного газа.

Газовый закон Генри точно соблюдается только для идеальных растворов и применим лишь в области невысоких давлений к газам, достаточно хорошо подчиняющимся законам Бойля – Мариотта и Гей-Люссака.

Таким образом, для разбавленного раствора фугитивность растворителя вычисляется по закону Рауля, а фугитивность растворенного вещества – по закону Генри. Константа Генри приобретает смысл фугитивности (давления) чистого растворенного вещества при давлении, равном общему давлению над раствором.