Геометрическая теория открытого резонатора

Рассмотрим общий случай резонатора, состоящего из двух сферических зеркал, имеющих радиусы R₁ и R₂ и расположенных друг от друга на расстоянии L. В приближении геометрической оптики внутри резонатора рассматривается луч, выходящий из т. Р₀ с координатой r₀ и углом α₀. После последовательных отражений от двух зеркал резонатора луч приходит в т. Р₁ с координатой r₁ и углом α₁.

Пользуясь матричным методом, можно найти условие устойчивости открытого резонатора. Если при любом выборе исходной точки (r₀,α₀), произвольная точка (r_n,α_n) не будет удаляться на бесконечно большое расстояние от оси, то резонатор считается устойчивым. Это означает, что луч претерпевает большое число отражений от зеркал, прежде чем он выйдет из резонатора.

В конечном итоге условие устойчивости резонатора сводится к выполнению неравенства: 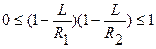(1.96)

где g₁=1-L/R₁, g₂=1-L/R₂ (1.97)

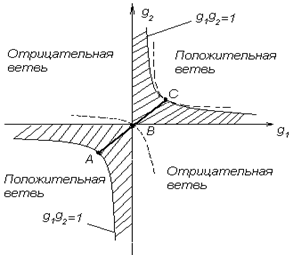
Рис.1.27. Диаграмма устойчивости на плоскости g1 и g2 для обобщенного сферического резонатора.

На рис. 1.27 приведена диаграмма в координатах g₁ и g_{2 ,} соответствующая уравнению (1.96). Заштрихованные области определяют устойчивые конфигурации открытого резонатора.

Особый интерес представляет класс сферических резонаторов, которым на рисунке соответствуют точки на прямой линии АС, составляющей угол 45⁰ с осями g₁ и g₂. Эта прямая описывается уравнением g₁=g₂ (так что R₁=R₂), а соответствующие ей резонаторы составлены из зеркал, имеющих одинаковые радиусы кривизны (симметричный резонатор). Из всех симметричных резонаторов рассмотрим более подробно те, которым соответствуют на рис. точкам А, B и C. Из приведенной ниже таблицы следует, что точке А соответствует концентрический резонатор (R=2L), точке В - конфокальный (R =L) , а точке С - плоский резонатор (R=¥). Следовательно, все эти три типа резонаторов лежат на границе, разделяющей устойчивую и неустойчивую области. В связи с этим часто используют не конфокальный, а квазиконфокальный резонатор, в котором расстояние между зеркалами увеличивают или уменьшают по сравнению с расстоянием, которое используется в конфокальном резонаторе. Другую конфигурацию, которую можно использовать, чтобы избежать неустойчивой области, представляет собой полуконфокальный резонатор (R₁=¥ и R₂=2L).