Добротность открытого резонатора

Как и любую колебательную систему, ОР можно охарактеризовать добротностью. Рассмотрим плоскопараллельный резонатор, в котором каждую моду можно представить как суперпозицию двух волн, распространяющихся в противоположных направлениях.

Пусть I₀-начальная интенсивность одной из этих волн, r₁ и r₂- коэффициенты отражения (по интенсивности) двух зеркал, T_i- относительные внутренние потери за проход вследствие дифракции. Тогда интенсивность I(t₁) в момент времени t₁=2L/c, т.е. после одного полного прохода резонатора, запишется в виде: I (t₁) =r₁r₂ (1-T_i)²I₀ (1.72)

Интенсивность после m полных проходов, т.е. в момент времени t_m=2mL/c равна I(t_m)=[r₁r₂(1-Т_i)²]^mI₀ (1.73)

Если q(t)- полное число фотонов в резонаторе в момент времени t, то, разумеется, оно пропорционально интенсивности, т.е. q(t)~I(t) и в соответствии с (1.73) можно написать следующее выражение:

q(t_m) = [r₁r₂ (1-Т_i)²]^mq₀ (1.74)

где q₀-число фотонов, изначально присутствовавших в резонаторе.
С другой стороны, число фотонов в момент времени t_m равно

q(t_m) =q₀exp(-t_m/τ_c), (1.75)
где τ_c - время жизни фотона в резонаторе

Из сравнения двух последних выражений и с учетом, что 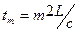получим: [exp(-2L/cτ_c)]^m=[r₁r₂(1-T_i)²]^m.

Отсюда находим: 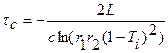(1.76)

Проведем оценку τ_с. Например, если выбрать r₁=r₂=r=0,98 и T_i≈0, то из (1.76) получим: τ_с=t_T/(-lnr)=49,5t_T, где t_T=L/c. Если положить L=90 см, c=3·10⁸ м/c, то t_T=3нс и τ_с≈150 нс. Из этого примера видно, что время жизни фотона много больше времени одного прохода резонатора.

Если предположить, что соотношение (1.75) справедливо не только в момент времени t_m, то и в любой момент t, то можно написать

q (t) ≈q₀exp(-t/τ_c), (1.77)

Тогда временную зависимость электрического поля в произвольной точке внутри или вне резонатора можно представить в виде:

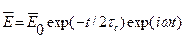. (1.78)

Определим теперь понятие добротности резонатора. Для любой резонансной системы и в частности для ОР, добротность Q определяется следующим образом.

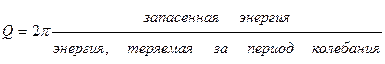. (1.79)

В нашем случае запасенная энергия равна q·hν, а энергия, теряемая в течение одного периода колебаний равна: hν(-dq/dt)T=hν(-dq/dt)/ν= -hdq/dt
тогда из (1.79) 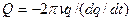(1.80)

Из (1.77) dq/dt= 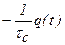и используя соотношение 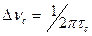, окончательно получим для добротности: Q=2πντ_c = ν/∆ν_c (1.81)

Таким образом, добротность резонатора равна отношению резонансной частоты ν к ширине линии резонатора ∆ν_с.

Для рассмотренного выше примера τ_с=150 нс, и положив ν=5·10¹⁴ Гц, получим Q≈5·10⁸.

С учетом (1.76) формулу добротности можно представить в виде:

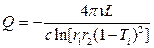. (1.82)

При T_i 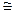0, r_i=1 имеем: 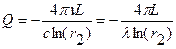(1.82а)