Волновая теория открытого резонатора

Считая, что дифракционных потерь нет (это соответствует бесконечно большим размерам зеркал), рассмотрим суперпозицию плоских волн, распространяющихся между зеркалами З₁ и З₂ плоскопараллельного открытого резонатора (резонатор Фабри-Перо) с базой L. (рис. 1.18).

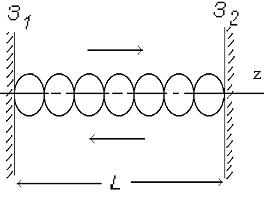
Рис.1.18.Формирование стоячей волны в резонаторе.

а) Сначала учтем только плоские волны, распространяющиеся строго вдоль оси резонатора z. За один цикл обхода волны от левого зеркала до правого и обратно изменение фазы волны составит величину:

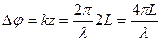
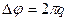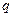Условие резонанса требует, чтобы волна вернулась в исходную точку в той же фазе, т.е. , где = 1,2,3… Приравняв правые части этих формул, получим: 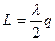. (1.83)

Это условие можно записать через частоту: 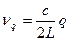, (1.84)

где 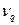- резонансная частота, соответствующая колебанию с номером .

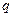Эти собственные частоты резонатора называются продольными модами резонатора. Они отличаются одна от другой лишь распределением поля вдоль оси z, т.е. в продольном направлении.
Величина ∆ν=ν_q+1-ν_q, 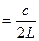(1.85) определяет расстояние по частоте между двумя соседними колебаниями.

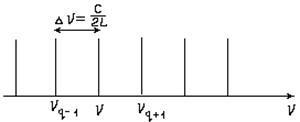Таким образом, спектр собственных колебаний открытого резонатора состоит из равноотстоящих друг от друга линий и является эквидистантным (рис.1.19).

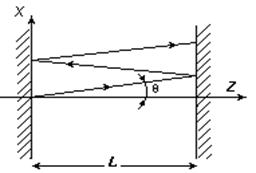б) Можно себе представить, что помимо продольных колебаний существуют также колебания, образованные плоскими волнами, распространяющимися под некоторым углом q к оси резонатора (рис.1.20).

Собственные частоты этих колебаний определяются условием:

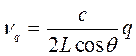, (1.86)

где q может принимать любые непрерывные значения. В результате сложения этих волн образуются так называемые поперечные колебания или поперечные моды резонатора. Для более подробного изучения поперечных мод резонатора рассмотрим объемный резонатор с идеально проводящими боковыми стенками (рис.1.21).

Спектр частот собственных колебаний такого резонатора определяется условием:

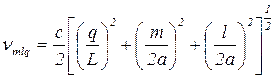, (1.87)

где m, l =0,1,2,3... целые числа.

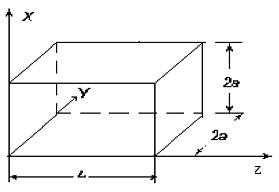
Рис.1.21. Схема объемного закрытого резонатора.

Приближенно, при малых углах распространения q и m,l<<q, можно считать, что моды открытого резонатора описываются модами прямоугольного резонатора.

Тогда резонансные частоты плоскопараллельного открытого резонатора можно найти из выражения (1.87) путем разложения его в степенной ряд:

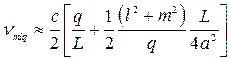. (1.88)

Из этого выражения можем найти разность частот между двумя модами, отличающимися только значениями числа m на единицу, в виде: 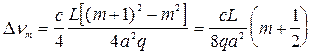. Учитывая, что 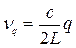, отсюда получим: 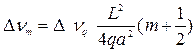. (1.89)

Аналогично получим, что для разности частот Dn_l:

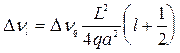. (1.90)

Эти моды будут отличаться только распределением поля в плоскости, ортогональной оси z, т.е. в поперечном направлении.

Спектр собственных колебаний (резонансных частот) плоскопараллельного резонатора с учетом формул (1.89) и (1.90) имеет вид, показанный на рисунке 1.22.

Величины Dn_m и Dn_l определяют разность частот между двумя последовательными поперечными модами.

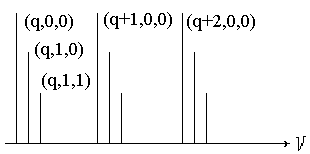
Рис.1.22. Спектр собственных колебаний плоскопараллельного открытого резонатора.