Дифракционная теория

Строгое рассмотрение электромагнитного поля в открытом резонаторе основывается на системе уравнений Максвелла с заданными граничными условиями на зеркалах. Лазерные резонаторы имеют ту особенность, что их характерные размеры (длина резонатора, радиусы кривизны и апертуры зеркал) намного превышают длину волны излучения. Исходя из этого, можно считать, что электромагнитное поле в резонаторе является поперечным, однородно поляризованным. Для вычисления его стационарного распределения на поверхности одного из зеркал в виде интеграла от поля заданного на поверхности другого зеркала, можно воспользоваться скалярной формой принципа Гюйгенса-Френеля. Такие расчеты были впервые проведены Фоксом и Ли.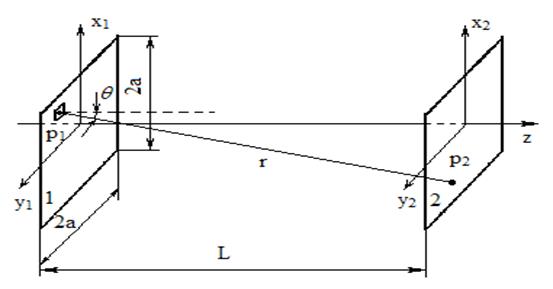

Рис. 1.23. К расчету плоскопараллельного резонатора с помощью дифракционного интеграла Кирхгофа.

Поле U_Р в любой р-ой зоне Френеля второго зеркала, обусловленное освещенным первым зеркалом, описывается поверхностным интегралом (дифракционный интеграл Кирхгофа):

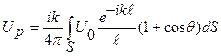(1.91)

где 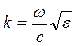- вектор распространения волны в среде; 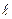- расстояние от точки на первом зеркале до точки наблюдения: θ - угол между 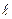и перпендикуляром к поверхности первого зеркала; U₀-поле в плоскости первого зеркала. Моды резонатора соответствуют стационарным решениям интеграла (1.91).

Структуру поля для разных мод рассчитывают методом последовательных приближений с использованием ЭВМ. Следует отметить, что метод последовательных приближений здесь в некоторой степени адекватен самому физическому процессу в резонаторе при нарастании количества отражений. На рисунке 1.25 представлен результат расчета Фокса и Ли для амплитуды поля в точке x=a/2 на поверхности одного из зеркал в зависимости от числа отражений. Видно, что с увеличением количества отражений амплитуда поля принимает постоянное значение. После N прохождений, когда установился стационарный режим, можно написать соотношение: 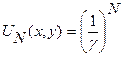υ(x,y), где γ - комплексная постоянная, υ(x,y)-функция установившегося распределения. Подставляя ее в (1.91), получим: 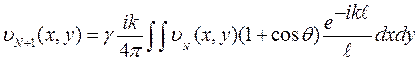. Поскольку υ_N+1=υ_N, индексы в дальнейшем будем опускать и для нахождения структуры поля на поверхности зеркал, получаем интегральное уравнение: 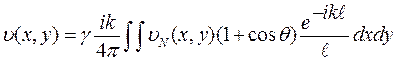(1.92)

Собственные функции υ_mn(x,y), являющиеся решением интегрального уравнения (1.92) при соответствующих значениях γ_mn (собственные значения), характеризуют структуру поля на поверхности зеркал резонатора и обозначаются как колебания типа TEM_mn. (рис.1.25). Каждая поперечная мода включает в себя ряд продольных мод, которым соответствуют разные q.

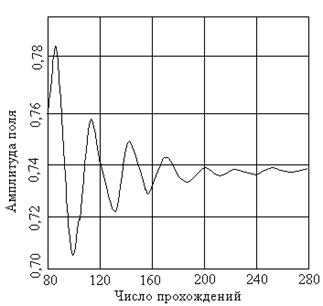
Рис.1.24. Изменение амплитуды поля в зависимости от числа прохождений.

Для прямоугольных зеркал индекс m означает число изменений направления поля вдоль оси x, а индекс n – вдоль оси y. В случае круговых зеркал n означает число изменений направления поля по окружности (для фиксированного радиуса), а m- вдоль радиуса.

Логарифм собственных значений γ_mn является комплексной величиной

lnγ_mn=β_mn+i(α_mn+kL), (1.93)

где β_mn определяет затухание за один проход, связанное с дифракционными потерями для каждой моды резонатора; α_mn определяет фазовый сдвиг за один проход, который прибавляется к геометрическому фазовому сдвигу.

Параметр β_mn характеризует добротность резонатора: 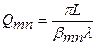. (1.94)

Из условия резонанса можно определить собственные частоты мод, которые выражаются через α_mn: 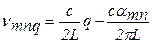. (1.95)

Таким образом, решение интегрального уравнения (1.92) для соответствующей конфигурации оптического резонатора дает информацию о структуре поля, резонансных частотах и дифракционных потерях резонатора. Заметим, что это уравнение имеет общий характер. Оно не связано с конкретной конфигурацией резонатора и формой зеркал и поэтому пригодно не только для плоских зеркал (резонатор Фабри-Перо), но и для зеркал иной формы (в частности, сферических).

На рис.1.26 показано распределение интенсивности для поперечных мод TEM_mn открытого резонатора.

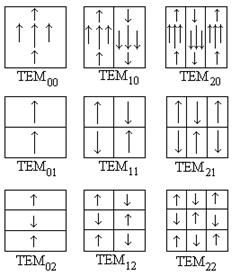Рис.1.25.Конфигурация электрического поля различных мод для квадратных зеркал.

Рис.1.26. Структуры электрических полей поперечных типов колебаний оптического резонатора.