Кинетические уравнения для населенностей уровней

Для анализа условий возникновения инверсной населенности в рассмотренных схемах оптической накачки составляются кинетические (балансные) уравнения, описывающие скорости изменения населенностей всех уровней в процессе накачки. Рассмотрим для примера трехуровневую схему накачки.

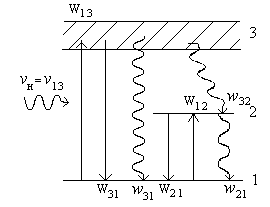
Рис.1.14.Схема переходов в трехуровневой схеме оптической накачки.

Вероятности для вынужденных переходов (W_ij) и вероятности процессов релаксации (w_ij) на этом рисунке приведены с учетом особенностей оптического диапазона, для которого характерны большие расстояния между квантовыми уровнями (Е_i-E_j>>kT). Скорости изменения населенностей квантовых уровней описываются следующими уравнениями:

DN3/dt=W₁₃ (N₁-N₃)-w₃₂N₃-w₃₁N₃

DN2/dt=W₂₁ (N₁-N₂) +w₃₂N₃-w₂₁N₂

DN1/dt =W₂₁ (N₂-N₁) +W₁₃ (N₃-N₁) +w₂₁N₂+w₃₁N₃ (1.64)

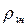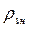где учтено, что W₁₂=W₂₁, W₁₃=W₃₁= B13, - спектральная объемная плотность энергии излучения накачки. Для определения порогового уровня накаfreакуимс нра5 ччки, при котором достигается инверсия населенностей между вторым и первым уровнями, т.е. N₂>N₁, достаточно проанализировать случай, когда под действием сильного излучения накачки установится стационарный режим, характеризирующийся условием dN_i / dt=0.

Тогда система(1.64) сводится к виду:

W₁₃ (N₁-N₃)-w₃₂N₃-w₃₁N₃=0

W₂₁ (N₁-N₂) +w₃₂N₃-w₂₁N₂=0

N₁+N₂+N₃=N₀ (1.65)

В этой алгебраической системе уравнений третье уравнение системы (1.64) заменено уравнением, определяющим полную населенность N₀ в рассматриваемой системе.

Дальнейшее упрощение полученной системы связано с тем обстоятельством, что при dN₃/dt=0 накопления частиц на третьем уровне не происходит, поэтому остается справедливым условие N₃<<N₁. Тогда система(1.65) приводится к виду:

W₁₃N₁-N₃(w₃₂+w₃₁)=0

W₂₁ (N₁-N₂) +N₃w₃₂-N₂w₂₁=0

N₀ ≈N₁+N₂ (1.66)

Из этой системы находятся N₁ и N₂, а затем величина ∆= N₂- N₁, определяющая инверсию населенностей между вторым и первым уровнями: 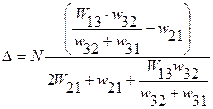(1.67)

Возможность инверсного заселения второго уровня, используя механизм накачки через третий уровень, определяется выполнением физического условия, при котором вероятность релаксации с третьего уровня на второй должна быть значительно больше вероятности релаксации с третьего уровня обратно на первый, т.е. w₃₂>>w₃₁.

При этом w₃₂=w₃₂^би+w₃₂^изл=w₃₂^би+A₃₂ (1.68)

гдеw₃₂^би-вероятность безызлучательных переходов, а w₃₂^изл=А₃₂ - вероятность спонтанных переходов. В рассматриваемой схеме должно выполняться условие w₃₂^изл≈0, т.е. w₃₂≈w₃₂^би (вероятность релаксации 3→2 должна быть в основном безызлучательной).

Для перехода 2→1 наоборот основную роль должны играть излучательные переходы, т.е. w₂₁ = w₂₁^би+A₂₁≈ A₂₁

C учетом сказанного, формула (1.68) принимает вид:

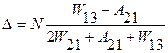(1.69)

Отсюда ∆=(N₂-N₁)>0, если W₁₃>A₂₁=1/τ₂₁^сп (1.70)

Так как W₁₃= 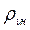B_13, то условие (1.70) можно представить в виде, которое определяет пороговый уровень накачки для достижения состояния с инверсией населенностей: 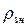^пор≥ 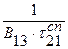(1.71)

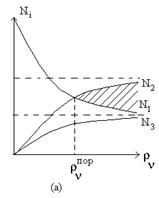
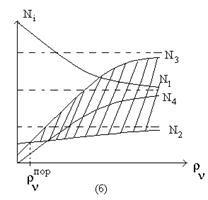
На рис.1.15. представлены графики изменения населенностей в трехуровневой (а) и четырехуровневой (б) схемах в зависимости от уровня накачки. Заштрихованные области соответствуют состоянию с инверсией населенностей квантовых уровней.

Рис. 1.15. Графики изменения населенностей.