Модели открытого текста
В качестве информации, подлежащей криптографическому преобразованию, будут рассматриваться сообщения или тексты. Термин текстили сообщение обозначает упорядоченный набор элементов алфавита, непустого конечного множества символов, используемых для кодирования информации.
На практике наиболее часто используются следующие алфавиты:
· бинарный ‑ Z2 = {0,1};
· шестнадцатеричный ‑ Z16={0,1,…,A,B,C,D,E,F};
· 26 букв латинского алфавита ‑ Z26={A,B,C,…,X,Y,Z};
· усеченное множество букв кириллицы ‑ Z32={A,Б,B,Г,…};
· множество символов, входящих в стандартные коды ASCII ‑ Z256.
В общем случае, если не оговорено иное, будем полагать, что алфавитом сообщений, подлежащих зашифрованию, является кольцо вычетов Zm={0,1,…,m-1}, а величину m будем называть мощностью или модулем алфавита исходных текстов.
Необходимо отметить, что реальные сообщения для любого конкретного языка, характеризуются определенной избыточностью. Статистика частот встречаемости элементов сообщений свидетельствует об их неравномерном распределении.
В частности, для достаточно большого объема литературного текста на русском языке наиболее часто встречающимися буквами оказываются {о,и}, среди наиболее часто встречающихся букв английского языка символы {e,t} (таблица 1).
Таблица 1
Относительные частоты встречаемости букв английского языка
(выборка 300 000 букв газетно-журнального текста)
| E | 12.7% | D | 4.2% | P | 1.9% |
| T | 9.0% | L | 4.0% | B | 1.5% |
| A | 8.2% | U | 2.8% | V | 1.0% |
| O | 7.5% | C | 2.8% | K | 0.8% |
| I | 7.0% | M | 2.4% | Q | 0.1% |
| N | 6.7% | W | 2.4% | X | 0.1% |
| S | 6.3% | F | 2.2% | J | 0.1% |
| H | 6.1% | G | 2.0% | Z | 0.1% |
| R | 6.0% | Y | 2.0% |
Отмеченные свойства языков используются криптоаналитиками при вскрытии шифров, поэтому для оценки свойств шифрованных текстов необходимо иметь соответствующую информацию о вероятностных характеристиках открытых сообщений.
С указанной целью используется ряд математических моделей открытых текстов, приведем примеры наиболее распространенных моделей, характеризующих их важные вероятностно-статистические свойства:
1. Открытый текст T={t1,t2,…} является последовательностью полиномиальных испытаний на множестве исходов Zm={0,1,…,m-1} с вектором вероятностей встречаемости отдельных знаков 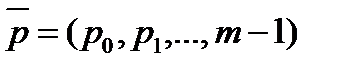 , где:
, где:
| pj=P{ti=j} |
Это одна из наиболее распространенных моделей открытого текста, которая позволяет решать задачи, связанные с классом поточных шифров (см. раздел «Классификация шифрсистем»).
Отметим, что применительно к схеме независимых испытаний используется характеристика неопределенности или мера информации, извлекаемой из эксперимента. Энтропией вероятностной схемы
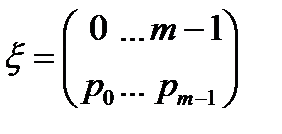
|
называется величина H(ξ):
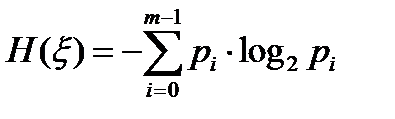
|
Согласно теореме кодирования любой исход вероятностной схемы может быть закодирован символами 0 и 1 так, что полученная длина кодового слова будет сколь угодно близка сверху к H(ξ). Итак, единицей количества информации логично считать один бит.
Нетрудно показать, что функция энтропии выпукла вверх и достигает своего максимума log2m для равновероятного распределения (1/m,…,1/m).
С энтропией связана еще одна характеристика – избыточность языка R, которая вычисляется по формуле:

|
Понятие избыточности языка возникло в связи с тем, что максимальная информация, которую мог бы нести каждый символ сообщения, в равновероятной схеме равен H=log2m. Для реальных текстов буква несет меньше информации, поэтому величина log2m-H характеризует неиспользованные возможности в передаче текста, а отношение
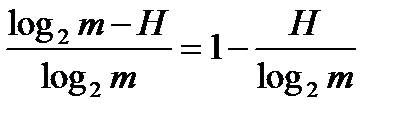
|
условно говоря, показывает, какую долю символов сообщения можно пропустить без существенной потери смысла.
В частности, очевидно, что вычеркивание из текста на русском языке всех гласных букв практически не снижает его информативности. Более того, в некоторых языках до 70-80 % знаков текста можно удалить без существенной потери смысла. Как следствие, для m-буквенного алфавита количество смысловых текстов (с заданными ограничениями на встречаемость букв) значительно меньше числа всевозможных наборов из N букв: mN. Согласно теореме Мак-Миллана число открытых текстов для реального языка с величиной энтропии на один знак текста H для достаточно больших N оценивается величиной #N:
| #N=2NH |
2. Другая модель ‑ открытый текст T={t1,t2,…,tv,tv+1,tv+2,…,t2v,…} является последовательностью независимых испытаний на декартовом произведении множеств:

|
которое называется множеством v-грамм. При этом, по крайней мере, для некоторых v-грамм (ti1,ti2,…,tiv) имеет место:
| P{(ti1,ti2,…,tiv)≠pi1pi2 …piv |
Модель обычно используется при анализе шифров блочного типа.
3. Еще одна модель ‑ открытый текст T={t1,t2,…} является последовательностью испытаний, связанных в простую однородную цепь Маркова с начальным вектором распределения вероятностей 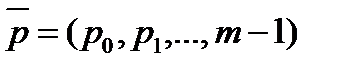 и матрицей переходных вероятностей
и матрицей переходных вероятностей 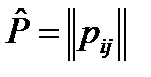 . Данная модель позволяет учитывать наличие зависимостей между знаками открытого текста, а потому используется для построения критериев, с помощью которых отбраковуются ложные варианты ключей.
. Данная модель позволяет учитывать наличие зависимостей между знаками открытого текста, а потому используется для построения критериев, с помощью которых отбраковуются ложные варианты ключей.
Статистические свойства реальных открытых текстов являются исходными данными для проведения криптоаналитических атак и оценки практической стойкости шифросистем.
Дата добавления: 2016-06-15; просмотров: 2577;











