Метод Прони для расчета собственных функций резонатора.

Рассмотренный выше метод Фокса-Ли дает возможность определить в линейном приближении два низших собственных типа колебаний – симметричный и антисимметричный.

Во многих случаях, в частности, при рассмотрении неустойчивых резонаторов этого оказывается недостаточно. Рассмотрим численный метод [3] решения интегрального уравнения (5.12).

Ŵ u_i = γ_i u_i

В силу численности метода примем, что распределение излучения в собственном типе колебаний задается вектором u_i, описываемым столбцом с количеством строк, равным числу точек, определяющих значение комплексной амплитуды на зеркале.

В этом уравнении Ŵ–симметричная комплексная матрица оператора формулы Кирхгофа. Порядок матрицы также определяется числом точек на зеркале, в которых задается функция u_i.

Сразу будем искать систему собственных векторов, ортонормированную относительно соотношения

(u_i , u_k) = 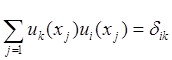, (7.13)

гдеδ_ik –символ Кронекера, равный 1 при i=k и 0 при i≠k.

Такое поточечное произведение отличается от обычного (скалярного) произведения, в котором один из векторов берется комплексно-сопряженным. Поэтому произведение произвольных векторов v (описывающих произвольные распределения комплексной амплитуды на зеркалах резонатора) в общем случае может быть комплексной величиной.

Свойство ортонормированности расширяет возможность использования системы собственных функций, поскольку позволяет найти коэффициенты k_i разложения произвольного вектора (произвольной функции) по собственным векторам (функциям). Действительно:

(u_k , v)= 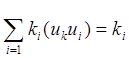(7.14 )

В качестве исходного для рассматриваемой процедуры возьмем распределение v₀ , получившееся в результате нескольких предварительно проведенных воздействий оператора Ŵ на произвольно заданное распределение v. При этом предположим, что в v₀ содержится уже лишь N наиболее добротных собственных значений собственных векторов (функций) u, после чего воздействуем на него еще N раз оператором Ŵ :

v₀ = k₁ u₁ + k₂ u₂ + … + k_N u_N + …

v₁ = k₁ γ₁ u₁ + k₂ γ₂ u₂ + … + k_N γ_N u_N + ………….. (7.15)

v_N = k₁ γ₁^Nu₁ + k₂ γ₂^Nu₂ + … + k_N γ_N^N u_N + …

Из полученных векторов мы можем получить их поточечные произведения, которые в силу ортогональности собственных значений будут иметь вид:

F_m = (v_m’ , v _m-m’) = K₁γ₁^m + K₂ γ₂^m+ … + K_N γ_N^m + … , (7.16 )

где K_i = k_i²_.

Из полученных N векторов можно получить 2N+1 таких произведений:

F₀ = K₁ + K₂ + … + K_N + …

F₁ = K₁γ₁ + K₂ γ₂ + … + K_N γ_N + …

F₂ = K₁γ₁² + K₂ γ₂² + … + K_N γ_N² + … ( 7.17)

F_2N = K₁γ₁^2N + K₂ γ₂^2N + … + K_N γ _N^2N + …

Вертикальные линии в (7.15) – (7.17) показывают, что мы ограничились рассмотрением N доминирующих собственных функций. То, что промежуточные значения F_m , где m ≠0, 1, 2N, 2N+1, могут быть получены в результате перемножения разных векторов, дает возможность контроля корректности расчетов.

Известно, что если есть N комплексных чисел γ_i, то может быть составлен многочлен N–й степени с коэффициентами Q_n, так, что γ_i будут корнями этого многочлена:

γ^N +Q₁ γ^N-1 + … + Q_N-1 γ ^N + Q_N = 0. (7.18)

Если подставить в этот полиномγ=γ_n и умножить на K_n γ_n^m, то получим часть вертикального столбца в правой части системы (7.17), с той лишь разницей, что каждый член столбца в правой части будет умножен на соответствующий коэффициент Q_N-i, где i меняется от 0 до N, если считать сверху вниз. Если провести такую операцию со всеми γ_n по очереди и сложить получившиеся столбцы, то станет очевидным, что величины F_m должны удовлетворять следующему соотношению:

F_m+N +Q₁ F_m+N-1 + … + Q_N-1 F_m+1 = F_m (7.19)

для тех же самых коэффициентов Q_i, причем для произвольных значений m. Это означает, что каждое F_m линейно зависит от предшествующих N значений F_m. Выписывая уравнения (7.19) для последовательных значений m = 1, 2 … N,получаем систему для N линейных уравнений:

Q₁F_N +Q₂ F_N-1 + … + Q_N F₁ = F_N+1

Q₁ F_N+1 +Q₂ F_N + … + Q_N F₂ = F_N+2 (7.20)

Q₁ F_2N-1 +Q₂ F_2N + … + Q_N F_N = F_2N

Теперь мы имеем все соотношения для вычисления собственных значений и собственных функций.

Процедура расчета строится следующим образом. Прежде всего по Nитерациям распределенияv₀вычисляются поточечные произведения F_m. После подстановки F_m в систему (7.20) вычисляются коэффициенты Q_i. Собственные значения γ_i получаются в результате решения уравнения (7.18) при известных Q_i. Решая (7.17) как систему уравнений при известных F_mи γ_i находим коэффициенты разложения k_i .И, наконец, собственные функции получаются решением линейной системы уравнений (7.15).

Таким образом рассмотренный метод позволяет получать любое наперед заданное число N собственных колебаний резонатора и соответствующих им собственных значений. Практически это число ограничивается возможностями вычислительной техники и количеством машинного времени. Следует отметить, что проведенные расчеты для 5-6 собственных типов колебаний резонатора позволяют в большинстве случаев получить достаточную для практического использования информацию. Посмотрим, что дает подобное рассмотрение для неустойчивых резонаторов [3].