Основы теории формы и ширины линии излучения

Вероятность спонтанного перехода в единицу времени определяется константой A₂₁, т.е. 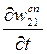=A₂₁ и в результате такого перехода испускается монохроматическое излучение с частотой 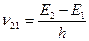(рис.1.3а). На самом деле происходит уширение линий излучения вследствие различных физических причин, приводящих к конечной ширине энергетического уровня. С учетом этого вероятность перехода в единицу времени и в расчете на единичный интервал частот с испусканием фотона в частотном интервале от ν до ν+dν определяется формулой:

(dw₂₁^cn/dt)_νdν=A₂₁g(ν) dν (1.23)

где g(ν)-так называемая функция формы линии излучения, определяющая частотное распределение излучения (рис.1.3б).

Таким образом, возникают две задачи:

1) исходя из определенной физической модели, найти функцию g(ν);

2) найти ширину линии излучения.

При этом под шириной линии излучения понимают интервал частот ∆ν, в пределах которого интенсивность излучения (или нормированная на максимальное значение относительная интенсивность) уменьшается до половинного значения, т.е. ∆ν=ν^″-ν΄ (рис.1.3, б).

Рис.1.3 (а) Линия монохроматического излучения,

(б) Спектр излучения с учетом уширения квантовых уровней.

“Естественное” уширение линии излучения

Фундаментальной причиной, приводящей к уширению линии излучения, является квантовый характер микрообъектов, подчиняющихся соотношению неопределенности Гейзенберга.

Действительно, это соотношение, записываемое в виде ∆p∆x~ħ, где ∆x и ∆p-неопределенности положения частицы и ее импульса, может быть представлено в виде ∆E ∆t~ħ, где ∆E–мера неопределенности энергии частицы, ∆t –время необходимое для проведения такого измерения.

Поскольку измерение энергии возбужденного состояния атома должно производится за время ∆t≤τ_сп, то из соотношения неопределенности получим: ∆E≤ħ/ τ_сп (1.24)

где τ_сп - среднее время жизни атома в данном состоянии. Так как τ_сп всегда конечно, то отсюда следует, что энергетические уровни имеют конечную ширину. (рис.1.4)

Рис.1.4 Энергетические уровни атомнойсистемы.

Из рис. 1.4 имеем: ∆ν=ν^”₂₁-ν^’₂₁= 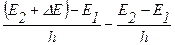=∆E/h (1.25)

Таким образом, из (1.25) и (1.24) получаем для оценки ∆ν формулу:

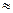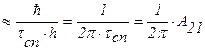Dn DE/h (1.26)

Найдем вид функции g(n), определяющей форму линии излучения.

В качестве модели излучающего атома в классической физике принимается осциллирующий диполь с радиационным затуханием, уравнение которого имеет вид: 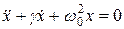, (1.27)

где х – координата, g - коэффициент затухания, w₀ – собственная частота системы. Решение (1.27) имеет вид: x=Cexp(-gt/2)exp(jw₁t), (1.28)

где ( при малом g).

Спектр G(w), соответствующий колебанию x(t), находится с помощью преобразования Фурье:

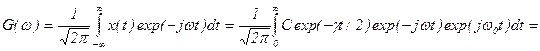
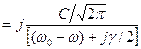. (1.29)

Отсюда спектральное распределение для интенсивности колебания

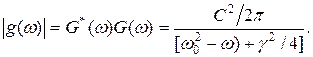(1.30)

Обозначив w₀=2pn₀, w=2pn, g=2pDn_л и найдя постоянную С из условия нормировки , получаем окончательно:

g(n)= 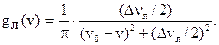(1.31)

Формула (1.31) соответствует так называемой лоренцевой форме линии излучения, что в формуле обозначено индексом «л». Из условия находим значения частот ν” и ν’. Тогда ширина линии излучения определяется соотношением:

(1.32)