Доплеровское уширение

В газах движение излучающих молекул относительно наблюдателя приводит к уширению линии за счет эффекта Доплера. Если скорость молекул равна u, то частота излучения, регистрируемая наблюдателем, рассчитывается по формуле: 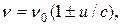(1.33)

где с - скорость света, n₀ - истинная частота атомного перехода (u<<c), а выбор знака зависит от того, в какую сторону движется молекула.

В газе атомы движутся с беспорядочно направленными скоростями, зависящими от температуры Т и распределенными в соответствии с законом Максвелла: 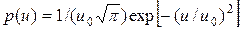, (1.34)

где 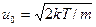- средняя тепловая скорость атомов с массой m, k - постоянная Больцмана.

Распределение частиц в газе по скоростям в результате эффекта Доплера определяет частотное распределение в излучении атомов, т.е. можно написать 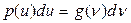(1.35)

где g(n) функция формы линии излучения.

Из (1.33) и (1.35) получаем g(n)=(c/n₀)p(u). Подставив вместо 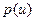формулу (1.34), имеем: 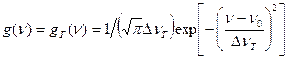, (1.36)

где Dn_Т=n₀u₀/с - доплеровский сдвиг частоты для частиц со средней тепловой скоростью. Формула (1.36) соответствует гауссовой форме линии излучения (что в формуле отмечено индексом «Г»).

Из условия 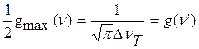определяется ширина линии излучения: 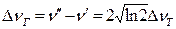(1.37)

Проведем сравнение линий излучения гауссовой и лоренцевой форм при их одинаковой ширине. Считая ∆ν_л=∆ν_Г. из (1.31) находим максимальное значение функции 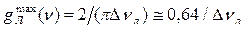(1.38)

Аналогично из (1.36) 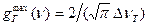. Подставив вместо 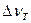его значение из формулы (1.37), получим: 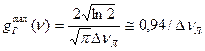(1.39)

На рис.1.5 построены графики лоренцевой и гауссовой линии излучения, приведенные к одинаковой ширине.

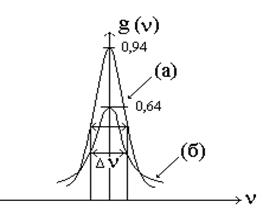
Рис.1.5. Графики гауссовой (а) и лоренцевой (б) линий излучения при ∆νл=∆νГ.

Как видно из графика при одинаковых ширинах гауссова кривая заострена сильнее лоренцевой

1.5 Коэффициенты Эйнштейна.
Термодинамическое рассмотрение

Рассмотрим связь между коэффициентами А₂₁, В₁₂ и В₂₁ используя термодинамический поход Эйнштейна. Предположим, что рассматриваемая среда помещена в полость (абсолютно черное тело) объемом V, стенки которой поддерживаются при температуре Т (термостат). Как только система достигает термодинамического равновесия, в ней установится излучение, спектральная объемная плотность которого 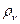определяется формулой Планка:

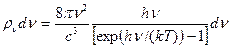(1.40)

где множитель 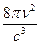определяет число типов колебаний в единице объема излучающей полости, а величина 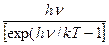дает среднюю энергию, приходящуюся на один тип колебаний.

Предположим, что квантовый ансамбль, находящийся в полости, является двухуровневой системой (рис.1.6). В такой квантовой системе, наряду со спонтанным излучением, будут происходить процессы вынужденного излучения и поглощения

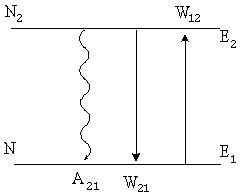
Рис.1.6 Схема квантовых переходов в двухуровневой квантовой системе.

Количество переходов 2→1 в единицу времени составляет величину (А₂₁+ρ_νВ₂₁)N₂, а количество обратных переходов 1→2 равно ρ_ν В₁₂ N₁.

Поскольку система в целом пребывает в состоянии термодинамического равновесия, число переходов с уровня 1 на уровень 2 должно уравновешивать число переходов с уровня 2 на уровень 1, т.е.:

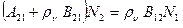(1.41)

Кроме того, согласно статистике Больцмана:

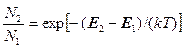(1.42)

Из этих двух выражений получаем: 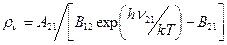(1.43)

Эйнштейн далее постулировал, что излучение, испускаемое или поглощаемое атомами при переходах между рассматриваемыми энергетическими состояниями, должно также подчиняться закону излучения Планка (1.40), так как атомы в рассматриваемой полости находятся в тепловом равновесии с окружающей средой.

Для согласования с формулой Планка необходимо выполнение следующих двух условий (при ν=ν₂₁): B₁₂=B₂₁=B (1.44)

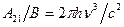(1.45)

Из формулы (1.44) следует, что вероятности поглощения и вынужденного излучения, связанные с излучением абсолютного черного тела, равны друг другу: W₁₂=W₂₁ (1.44a)

Соотношение (1.45) позволяет вычислить коэффициент А₂₁, если известен коэффициент В вынужденного излучения в поле излучения черного тела.

Таким образом, полная вероятность излучательных переходов в единицу времени равна:

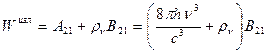(1.46)

Из формул W₁₂=s₁₂F, W₂₁ =s₂₁F, такжеследует, что s₁₂=s₂₁ (1.44б)

Таким образом, термодинамическое рассмотрение показывает равновероятность индуцированных излучения и поглощения и устанавливает количественную связь между коэффициентами Эйнштейна.

Квантомеханическое рассмотрение задачи о вычислении вероятности квантового перехода дает следующее значение для W_21:

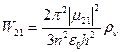, (1.47)

где 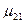- матричный дипольный момент атома.

Сравнивая (1.47) с формулой Эйнштейна для вероятности перехода W₂₁=r_nB₂₁ получим формулу, связывающую коэффициенты Эйнштейна с атомными характеристиками квантового ансамбля: 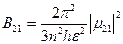(1.48)