Режимы движения жидкости и основы гидродинамического подобия
Существуют два режима течения жидкости — ламинарный и турбулентный.
При турбулентном режиме движения частицы жидкости перемещаются по траекториям, направленным вдоль общего течения, в частности, вдоль оси трубы без поперечного перемешивания.
При турбулентном режиме движения частицы жидкости перемещаются по случайным, неопределенно искривленным траекториям, имеющим пространственную конфигурацию. Движение имеет беспорядочный хаотический характер. Его особенность - наличие поперечных и продольных (относительно направления общего течения) пульсаций скорости и пульсаций давления, что существенно влияет на затраты энергии при перемещении жидкости.
Для анализа результатов эксперимента и описания режимов течения жидкостей и газов широко используется теория размерностей и подобия.
Размерность [а] любой физической величины а выражается через основные единицы измерения в виде степенного одночлена. В частности, в СИ размерность любой механической величины А имеет вид
[A] = La Mb Tg ,
где L, M, Т — единицы измерения длины, массы и времени соответственно.
Размерные физические величины
a1, a2, ... , ak (3.1)
называются величинами с независимыми размерностями, если размерность ни одной из них не может быть выражена через размерности остальных k - 1 величин из (3.1) .
В противном случае, т.е. если выполняется равенство
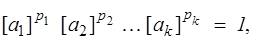 (3.2)
(3.2)
где не все рi равны нулю, величины (3.1) будут размерно зависимы.
Если число основных единиц изменения равно т, то k £ т.
Для описания многих явлений в гидромеханике достаточно трех основных единиц измерения: длины, массы, времени. В этих случаях число величин с независимыми размерностями не может быть более трех.
П-теорема теории размерностей.
Всякая зависимость вида
A = ¦ (a1, a2, … ,ak, ak+1, … ,an),
имеющая физический смысл, в которой величины a1, a2, ... , ak обладают независимыми размерностями, может быть представлена в виде
П = F (П1, п2, … , Пn – k), (3.3)
где величины П, П1 , П2, ..., Пn-k — обладают нулевыми размерностями и определяются по формулам

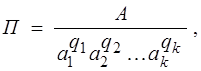
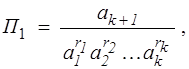
………………….
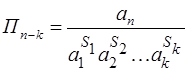 (3.4)
(3.4)
Два явления подобны, если по заданным характеристикам одного можно получить характеристики другого простым пересчетом, который аналогичен переходу от одной системы единиц измерения к другой системе.
Необходимые и достаточные условия подобия двух явлений, условно называемых "модель" и "натура", имеют вид
П1м = П1н П2м = П2н , … , П(n – k)м = П(n – k)н, (3.5)
где Пiм — безразмерные параметры (3.4), рассчитанные для "модели", а Пiн — для "натуры".
Величины Пi называются критериями подобия, а условия (3.5) —условиями подобия.
Основными критериями подобия при установившемся течении вязкой несжимаемой жидкости являются:
при течении по трубам число Рейнольдса
Re = ruL/m
при течении в открытых каналах число Фруда
Fr = u2/(gL) или 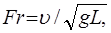 (3.6)
(3.6)
где r, m — соответственно плотность и вязкость жидкости; u — средняя скорость течения; L — характерный линейный размер; g — ускорение свободного падения.
В случае круглых труб обычно принимают L равным диаметру трубы.
Если живое сечение потока имеет некруговую форму, то числа Рейнольдса и Фруда обычно рассчитываются по формулам
Re = ru 4RГ/m, Fr = u2/(gL), (3.7)
где RГ — гидравлический радиус.
Если Re < 2320, то режим течения ламинарный. Если Re > 2320, режим турбулентный.
Вопросы по теме 3.
1 . Что такое параметры с независимыми размерностями?
2. Чему равно максимально возможное число параметров с независимыми размерностями?
3. В чем заключаются условия подобия двух явлений?
4. Какой вид примет формула (3.3) при n = k?
5. Как вычислить число Рейнольдса для некруглой трубы?
Дата добавления: 2016-11-26; просмотров: 2243;











