Гидравлический расчет простых напорных трубопроводов
Простым называется трубопровод, не имеющий ответвлений и с постоянными по длине диаметром и расходом. Длинным считается трубопровод, в котором потери напора в местных сопротивлениях малы по сравнению с потерями напора на трение по длине. В этом случае первыми или пренебрегают, или учитывают их через суммарную эквивалентную длину å lэкв , составляющую обычно 1—5 % от реальной длины трубопровода. В коротком трубопроводе оба вида потерь напора соизмеримы.
Самотечным называется трубопровод, перемещение жидкости в котором происходит только за счет сил тяжести.
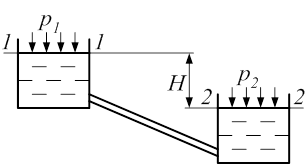
Рис. 6.1. Схема самотечного трубопровода
При гидравлическом расчете трубопроводов используются уравнение Бернулли (2.10), уравнение неразрывности и все понятия и формулы, рассмотренные в гл. 4. Такой расчет может быть сведен к решению одной из трех основных задач.
Задача 1. Определение необходимого действующего напора по заданным параметрам трубопровода и жидкости .
В качестве примера рассмотрим трубопровод на рис. 6.1.
Пусть жидкость с заданными свойствами (ρ, v или η) должна перетекать из верхнего резервуара в нижний (уровни в которых считаются постоянными) с заданным расходом Q по трубопроводу с известными параметрами l, d, D, åz или å lэкв. Давления р1 и р2 на свободных поверхностях жидкости известны. Примем, например, что p1 = р2 =pа.
Определить требуемый действующий напор.
Решение. Уравнение Бернулли для живых сечений, проходящих по свободным поверхностям жидкости в резервуарах, с учетом того, что p1 = р2 и u1 » u2 » 0 (из-за больших площадей живых сечений) принимает вид
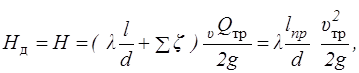 (6.1)
(6.1)
где u — скорость жидкости в трубопроводе.
Оно решается методами, рассмотренными в гл. 4.
Задача 2. Определение пропускной способности трубопровода Q по заданным параметрам его и жидкости.
Рассмотрим методику решения этого типа задач на примере рис. 6.1, но при заданном значении H и неизвестном значении Q.
Решение. Уравнение Бернулли по-прежнему имеет вид (6.1), но определению подлежит uтр, связанная с расходом соотношением Q= uтр sтр. В общем случае решение этого уравнения относительно uтрзатруднено, так как неизвестен вид зависимости и l и åz от Re, a следовательно, и от uтр .
Для преодоления этих трудностей существуют два способа — аналитический и графоаналитический.
Аналитически задача решается методом последовательных приближений. Он особенно прост и удобен, если в результате анализа исходных данных можно предположить или ламинарный режим движения, или квадратичную зону сопротивления. Ориентировочным признаком первого является высокая вязкость жидкости, второго — малая вязкость жидкости, значительная относительная шероховатость труб. Исходя из этих предположений, выражают l по формулам (5.3) или (5.7), а затем уравнение (6.1) разрешают относительно uтр . Для проверки правильности решения определяют Re и сравнивают его со значениями Reкр или 500 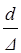 , в зависимости от выдвинутого предположения. Если предположение подтвердилось, определяют Q, если нет, то выдвигают уточненное предположение, расчет повторяется и т.д.
, в зависимости от выдвинутого предположения. Если предположение подтвердилось, определяют Q, если нет, то выдвигают уточненное предположение, расчет повторяется и т.д.
Задача аналитически легко решается при помощи ЭВМ, в том числе и таких простых, как программируемые микрокалькуляторы.
Графоаналитический способ решения основан на предварительном построении графической зависимости hпот=hпот(Q), называемой гидравлической характеристикой трубопровода. Для этого последовательно задаются рядом произвольных значений Q, по которым, используя схему Q®u ® Re®l® hпот, вычисляют соответствующие им значения hпот. По этим данным строится график hпот = hпот (Q) (рис. 6.2), отложив на оси ординат которого известное значение Hд, на оси абсцисс находят соответствующее ему искомое значение Q.
Задача 3. Определение минимально необходимого диаметра трубопровода по заданным действующему напору, параметрам жидкости и трубопровода, а также по его требуемой пропускной способности.
Рассмотрим эту задачу на примере рис. 6.1.
Аналитическое решение при ручном счете затруднено, так как в уравнение (6.1) искомый диаметр входит не только явно, но и косвенно (от него зависят u, l и z ).
При графоаналитическом способе, задаваясь рядом значений d и вычисляя по ним hпот, строят по этим данным графическую зависимость hпот = hпот (d) и по этому графику (рис. 6.3) определяют значение d, соответствующее заданной величине Hд.
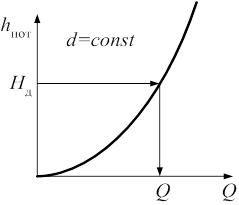
Рис. 6.2. Гидравлическая характеристика простого трубопровода
При решении задачи любого типа может оказаться, что в каком-либо сечении трубопровода давление в жидкости окажется меньше (или равным) давления насыщенных ее паров pп при данной температуре. В этом случае жидкость вскипает и образуются полости, заполненные парами. Сплошность потока нарушается. Такое явление называется кавитацией. Для его предотвращения в трубопроводах, работающих или при давлении ниже атмосферного (сифонные сливы, всасывающие линии насосных установок), или транспортирующих сжиженные газы, необходимо поддерживать условие р > рпдля любого живого сечения, где под р понимается абсолютное давление. Проверка выполнения этого условия обычно проводится для "опасного" сечения, т.е. сечения, в котором давление наименьшее.
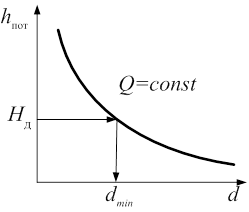
Рис. 6.3. Графическая зависимость потерь напора в простом трубопроводе от диаметра
Вопросы по теме 6.
1. Какие три основные задачи рассматриваются при расчете трубопроводов?
2. В чем заключается сущность графоаналитического метода расчета трубопроводов и какие задачи им решаются?
3. Какие признаки позволяют предположить ламинарное движение жидкости или квадратичную зону гидравлического сопротивления?
4. Что называется гидравлической характеристикой трубопроводов и каков принцип ее построения?
5. Каково дополнительное условие работы трубопроводов, если они работают при давлении ниже атмосферного?
6. Какое живое сечение трубопровода называется опасным?
Дата добавления: 2016-11-26; просмотров: 2874;











