Тема 10. Испытания в режиме вынужденных колебаний

Большую популярность приобрел метод, который заключается в том, что вместо приложения к образцу постоянного напряжения и измерения реологических характеристик в режиме установившегося течения образец подвергают осциллирующим напряжениям или деформациям. В реометрах, в режиме CS, приложенное напряжение может быть описано синусоидальной функцией времени:

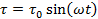
В этом случае реометр измеряет зависимость деформации от времени. Испытания с осциллирующими напряжениями часто называют “динамическими испытаниями”. Они представляют собой иной подход к измерению вязкоупругости, чем метод ползучести-восстановления. Оба вида испытаний дополняют друг друга, так как одни аспекты вязкоупругости хорошо описываются динамическими испытаниями, а другие - ползучестью и восстановлением.

При динамических испытаниях получают данные о вязкой и упругой реакциях образца в зависимости от скорости воздействия на него, иными словами, получают зависимость осциллирующего напряжения или деформации от заданной угловой скорости или частоты. Поскольку обычные измерения проводят не толькопри одной заданной частоте, а в широком диапазоне частот, они занимают довольно много времени.

В то время как измерение динамической вязкости ньютоновской жидкости в режиме установившегося ротационного течения (после достижения заданного уровня температуры) занимает одну или две минуты, измерение вязкоупругости полимера может занять в десять раз больше времени как в режиме динамических испытаний, так и при испытаниях ползучести и восстановления.

Следует иметь в виду, что при работе в области линейной вязко­упругости динамические испытания могут быть проведены как на CS-, так и на CR-реометрах с идентичными результатами. Проведение динамических испытаний на ротационном вискозиметре означает, что ротор, верхняя плита или конус больше не вращаются с постоянной скоростью в одном направлении, а попеременно отклоняются по синусоидальной временной функции* на малый угол ф вправо и влево. Это вызывает аналогичную синусоидальную деформацию образца, помещенного в измерительный зазор, и соответствующую синусоидальную картину изменения напряжений, амплитуда которых связана с природой испытуемого образца.

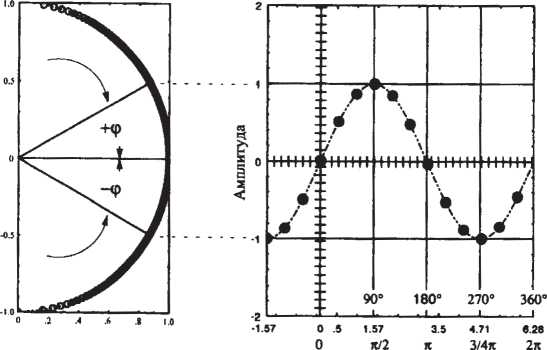
Чтобы не выйти за пределы области линейной вязкоупругости, угол отклонения ротора почти всегда очень мал, часто не более 1° (рис. 36).

Угловая скорость (1/с) Рис. 36. Динамические испытания: задание осциллирующих деформаций или напряжений

Из этого следует очень важный вывод, касающийся динамических испытаний и сферы их применения: в процессе динамических испытаний вязкоупругих жидкостей и даже твердых тел не только не происходит механического разрушения образцов, но и сохраняется их внутренняя структура. С реологической точки зрения структура испытуемых образцов находится как бы в “состоянии покоя”.

Некоторые теоретические аспекты динамических испытаний

Чтобы создать некую основу для интерпретации результатов ди­намических испытаний, проведем теоретическое обсуждение, используя модели спираль-демпфер (теоретически менее подготовленными читателями оно может быть опущено).

Как уже было показано, спираль моделирует упругую реакцию образца, определяемую как

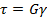
Демпферы моделируют реакцию ньютоновской жидкости, кото­рая определяется следующим образом:

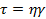
Упомянутые основные реологические элементы – как сами по себе, так и их различные сочетания – обсуждаются на этот раз с точки зрения динамических испытаний.

Модель спирали (рис. 37). Этот рисунок показывает, как спираль может подвергаться осциллирующей деформации, когда конец кривошипа, закрепленный на коленчатом валу, поворачивается на один полный оборот, а второй конец сжимает и растягивает пружину. Если угловая скорость равна со, а максимальная деформация пружины γ₀, то изменение деформации в функции времени можно записать как

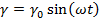
а зависимость напряжения в функции времени будет иметь вид

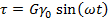
Эти зависимости в графическом виде представлены на рис. 37, откуда видно, что в случае этой модели деформация и напряжение совпадают по фазе: при максимальной деформации и результирующее напряжение также максимально.

Модель демпфера(рис. 38). Если заменить спираль на демпфер и двигать поршень с помощью аналогичного кривошипа, можно получить следующее уравнение:

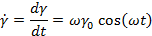
Подставляя это выражение в уравнение демпфера, получим

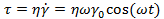
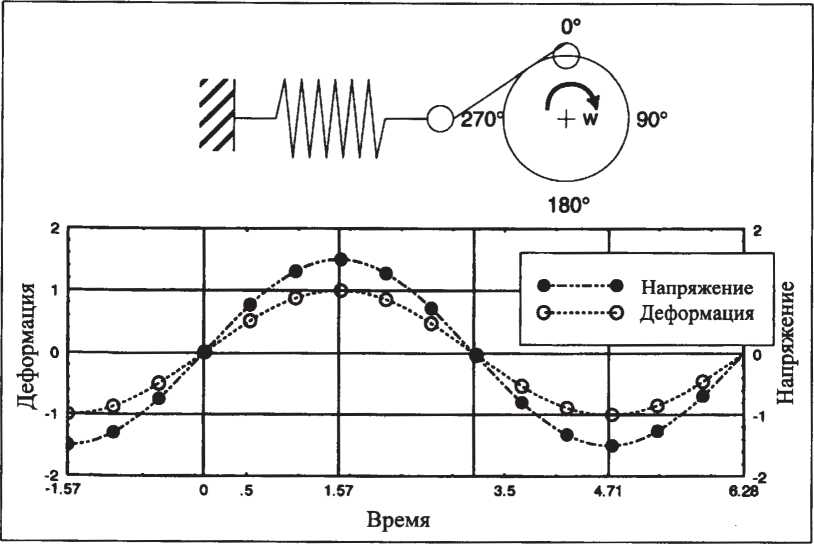
Рис. 37. Динамическое испытание: измерение напряжения в зависимости от заданной деформации для упругого твердого тела (пружины).

Рис. 38. Динамическое испытание: измерение напряжения в зависимости от заданной деформации для ньютоновской жидкости (демпфера).

Из рис. 38 очевидно, что напряжение (реакция демпфера на сдвиг) отстает от деформации на 90°. Это отставание также может быть выражено через угол сдвига фаз δ = 90°, на который заданная деформация опережает измеренное напряжение.

Уравнение может быть переписано следующим образом:

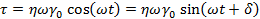
Всякий раз, когда деформация демпфера достигает максимума, скорость изменения деформации становится равной нулю (у = 0); когда же величина деформации, проходя через ноль, меняет знак с положительного на отрицательный, скорость ее изменения самая высокая, что приводит к максимальной величине напряжения.

Реакция тела называется упругой, если напряжение совпадает по фазе с деформацией. Если фаза между ними отличается на 90°, такое тело называют вязким. Если сдвиг угла фаз находится в пределах 0 < δ < 90°, такое тело называют вязкоупругим.

Модель Кельвина-Фойхта(рис. 39, кривая с точками в виде треугольников).

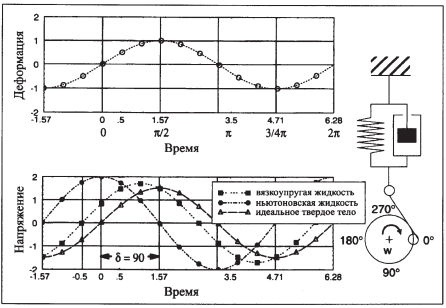
Рис. 39. Динамические испытания вязкоупругой жидкости, ньютоновской жидкости и идеального твердого тела в режиме CR (модель Кельвина-Фойхта).

Как было показано ранее, эта модель представляет собой комбинацию демпфера и спирали, соединенных параллельно. Общее напряжение равно сумме напряжений на обоих элементах, в то время как деформации равны.

Уравнение состояния имеет вид

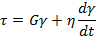
Введение синусоидальной зависимости деформации приведет к выражению

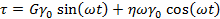
Из последнего уравнения следует, что реакция рассматриваемой модели, состоящей из двух элементов, либо упругая (δ= 0), либо вязкая (δ=90°).

Модель Максвелла (рис. 40, кривая с черными точками). Эта модель представляет собой комбинацию демпфера и спирали, соединенных последовательно, в которой общее напряжение равно напряжению на каждом элементе, а общая деформация есть сумма деформаций демпфера и спирали.

Рис. 40.Динамические испытания вязкоупругой жидкости, ньютоновской жидкости и идеального твердого тела в режиме CR (модель Максвелла).

Уравнение состояния для этой модели имеет вид

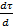+ = ωγ ₀cos(ωt)+ 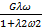cos⁡(ωt)

В этом уравнении член 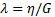обозначает время релаксации. Как и в модели Кельвина-Фойхта, напряжение как отклик на синусоидальную деформацию определяется двумя составляющими: упругой синусоидальной волновой функцией с φ = 0 и вязкой косинусоидальной волновой функцией с φ = 90°.

Реальные вязкоупругие жидкости (рис. 41, кривая с точками в виде черных квадратов) являются более сложными, чем тело Кельвина-Фойхта или жидкость Максвелла. Угол сдвига фаз у них находится в пределах 0 < δ < 90°, а величины G*(см. ниже) и δ зависят от частоты.

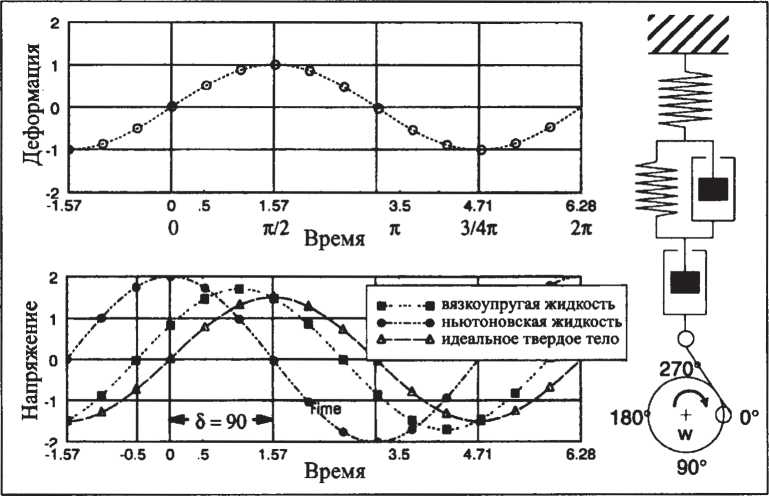
Рис. 41. Динамические испытания вязкоупругой жидкости, ньютоновской жидкости и идеального твердого тела в режиме CR(модель Бюргера)

В режиме CR-измерений деформация определяется амплитудой 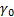и угловой скоростью ω:

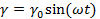
Результирующее напряжение характеризуется амплитудой на­пряжения 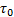и углом сдвига фаз δ:

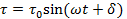
Угловая скорость связана с частотой колебаний следующим образом:

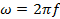
где частота f дана в Гц (1 Гц = цикл/с); размерность ω - 1/с или рад/с.

Значение ω, умноженное на время t,определяет угловую скорость как угловое отклонение в радианах: 2π соответствует полной окружности в 360°.

Обычно вводят термин «комплексный модуль G*, который оп­ределяют как

G*=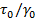

Величина G* представляет собой общее сопротивление образца приложенной деформации.

Необходимо напомнить, что у реальных вязкоупругих материалов как комплексный модуль, так и угол сдвига фаз зависят от частоты. Поэтому при нормальных испытаниях необходимо пройти определенный частотный интервал и получить зависимость измеренных величин G* и δ от частоты. Прохождение частотного интервала означает, что частоту деформирования ступенчато уве­личивают и на каждой ступени измеряют G* и δ.

Развертка G* и δ по частоте в пределах заданного интервала дает рабочие графики (рис. 42). Снижение δ в пределах всего диапазона от 0 до 90° в зависимости от частоты означает снижение вязкого и, соответственно, возрастание упругого вкладов в характеристику испытуемого образца. Заданная волновая функция деформации (в режиме CS-волновая функция напряжения) определяется по крайней мере по 150 экспериментальным точкам. Это в свою очередь, дает 150 значений напряжения, которые образуют синусоидальную волну, отличающуюся от волны деформации амплитудой и углом δ. Искомые величины G* и δ для каждых вводимых значени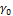й и 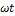определяют методом “кросс-корреляции гармонических сигналов”, который заложен в компьютерное программное обеспечение. Так как при любом новом значении частоты всегда необходимо получить один или два полных цикла, чтобы достичь равновесия, компьютерная программа обычно берет три цикла за­данной волны, чтобы получить достоверные значения G* и δ.

Это значит, что при малых значениях частоты, например ω = 0,001 с^-1 для измерения одного значения G* и одного значения δ необходимо 1000 с (около 16 мин) по одному циклу и более 3/4 ч – по трем циклам. В целях экономии времени такие испытания редко проводят при частотах ниже 0,01 с^-1.

Полученные на этом этапе результаты необходимо преобразовать в вязкую и упругую компоненты вязкоупругого поведения образца. Это лучше всего сделать посредством метода численного сглаживания Гаусса, часто используемого в математике и физике.

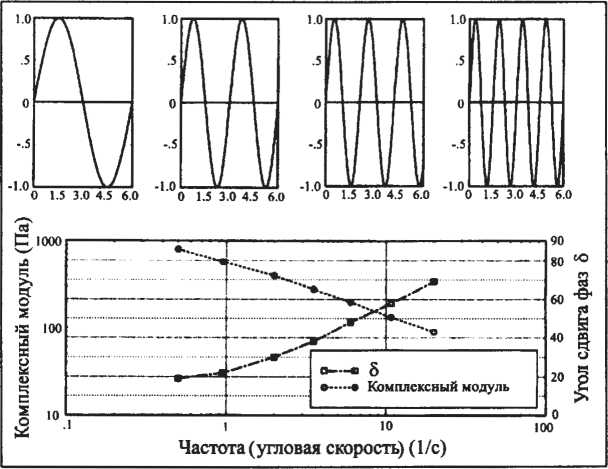
Рис. 42. Динамическое испытание: развертка по угловой скорости.

Применение метода численного сглаживания Гаусса для раз­деления вязкого и упругого поведения образцов, подвергнутых динамическим испытаниям(рис. 43). В этом методе пользуются комплексными числами, которые позволяют работать с корнем из отрицательного числа

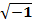=i

и комплексные числа могут быть представлены как векторы с действительными и мнимыми осями (компонентами).

Комплексный модуль G * может быть определен следующим об­разом:

)

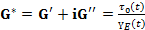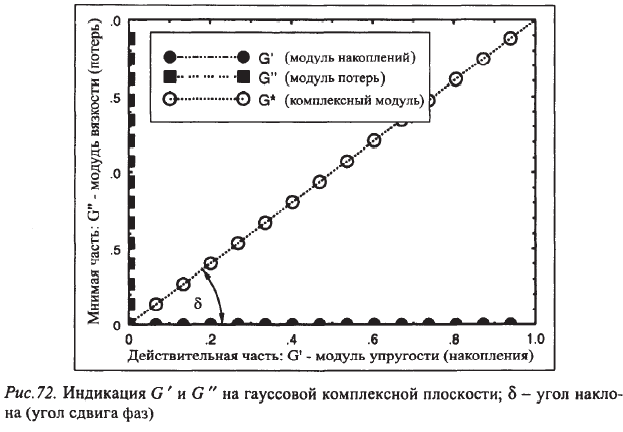
Рис.43. Индикация модулей накопления и потерь на гауссовой комплексной плоскости.

В этом уравнении величины G' и G"обозначают:

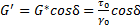- модуль упругости, или модуль накопления;

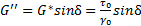- модуль вязкости, или модуль потерь.

Термин “модуль накопления” указывает на то, что энергия напряжения была временно запасена в процессе испытания, но она может быть впоследствии возвращена. Термин “модуль потерь” говорит о том, что энергия, использованная для инициирования течения, необратимо перешла в теплоту (“потеряна”).

Если вещество чисто вязкое, то угол сдвига фаз 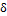= 90°:

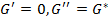
Если вещество чисто упругое, то угол сдвига фаз 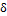= 0:

.

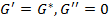Из комплексного модуля G* можно определить комплексную вязкость η|*:

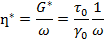
Комплексная вязкость отражает общее сопротивление динамическому сдвигу. Ее также можно разложить на две компоненты – запасенную (мнимую) вязкость 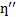(упругая компонента) и динамическую вязкость 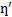(вязкая компонента):

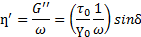
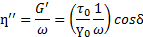
Зависимость динамических данных от угловой скорости. Ре­альные вещества не являются ни телами Кельвина-Фойхта, ни мак­свелловскими жидкостями, а представляют собой сложную комбинацию этих основных моделей. Чтобы оценить динамические характеристики реальных веществ, полезно рассмотреть поведение этих двух основных моделей при изменении угловой скорости.

При динамическом испытании тела Фойхта модули выражаются следующим образом: G' прямо связан с модулем пружины G, тогда как

G"= ƞω (рис. 44).

Из этого следует, что G' не зависит от частоты, тогда как G"линейно связан с частотой. При низких частотах поведение этого модельного вещества определяется поведением его пружины, т.е. упругая компонента G' превышает вязкую компоненту G". При промежуточной частоте величины обеих компонент равны, а при высоких частотах вязкая компонента становится преобладающей.

Используя равенство 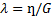, приведенное выше уравнение можно преобразовать

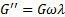
При динамическом испытании жидкости Максвелла модули в функции 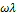, выражаются соотношениям

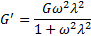
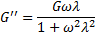
Когда член 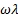, становится очень малым, используют член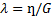

(вязкость демпфера/модуль пружины), тогда

Когда член 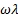становится очень большим, тогда

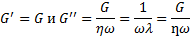
При низких частотах вязкая компонента G" выше, чем упругая 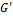. Максвелловская модель реагирует точно так же, как и ньютоновская жидкость, так как для реакции демпфера имеется достаточно времени, чтобы успеть отреагировать на заданную деформацию. При высоких частотах положения G' и G" меняются местами: модельная жидкость реагирует точно так же, как и единичная спираль, поскольку демпфер не успевает реагировать на заданную деформацию.

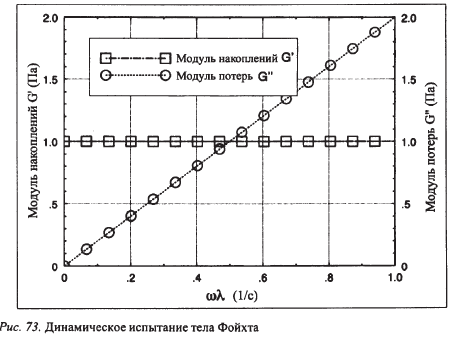
Рис. 44. Динамические испытания тела Фойхта.

Такое поведение представлено на рис. 45. На этом графике в двойных логарифмических координатах приведены зависимости обоих модулей в функции 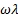. При низких частотах кривая запасенного модуля G' возрастает линейно с наклоном tgα = 2 и при высокой частоте асимптотически достигает величины модуля пружины G. Кривая модуля потерь G" сначала также линейно возрастает (tgа = 1), достигая максимума при 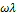= 1, а затем падает (tgα = -1). При 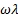= 1 оба модуля равны.

При оценке результатов динамических испытаний представляют интерес частота, при которой пересекаются кривые обоих модулей, и наклон частотных зависимостей, особенно при низких частотах.

Для очень низких значений угловой скорости по величине G" можно оценить динамическую вязкость демпфера ƞ= G"/ 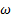и время релаксации 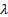= 1/( G" ).

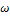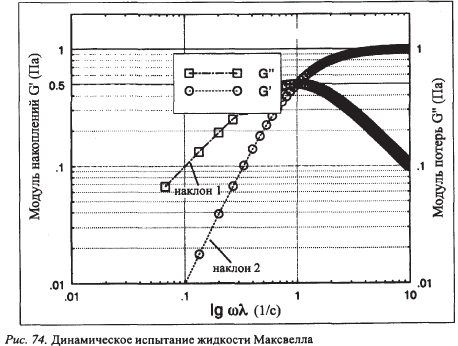
Рис. 45. Динамические испытания жидкости Максвелла

Соотношение Кокса—Мерца. Два ученых, которые дали этому соотношению свое имя, эмпирически установили, что вязкость при стационарном сдвиге, измеренная в зависимости от скорости сдвига, может быть непосредственно связана с динамической комплексной вязкостью ƞ*, измеренной как функция угловой скорости:

ƞ( 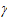) = ƞ*

Было обнаружено, что это соотношение справедливо для многих расплавов и растворов полимеров, но редко дает приемлемые результаты для суспензий.

Преимущество соотношения Кокса-Мерца состоит в том, что технически проще работать с частотой, чем со скоростями сдвига. На ротационных вискозиметрах невозможно проводить испытания расплавов и растворов полимеров при высоких скоростях сдвига из-за проявления эластичности – эффекта Вайссенберга. Поэтому вместо измерений кривой течения при стационарном сдвиге проще провести динамические испытания и использовать комплексную вязкость.

Определение области линейной вязкоупругости. В разделе, описывающем испытания ползучести и восстановления, было показано, насколько важно проводить измерения в области линейной вяз­коупругости. Эта область имеет также большое значение и при ди­намических испытаниях. Чтобы определить границу между линейной и нелинейной областями вязкоупругости, проведем одно простое исследование.

Вместо динамических испытаний с фиксированной амплитудой напряжения или деформации и разверткой по частоте может быть выполнено другое - с фиксированной частотой в 1 Гц и с разверткой по амплитуде. Амплитуда автоматически ступенчато возрастает после достижения установившихся значений деформации (напряжения). В результате подобных измерений получают зависимость G*от амплитуды.

На схематической диаграмме (рис. 48) кривая комплексного модуля сначала проходит параллельно оси абсцисс (в данном примере

lgG* = 0,5 и на этом участке не зависит от амплитуды), а при lg 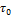= 1 начинает снижаться.

Рис. 48. Динамическое испытание: развертка по амплитуде напряжения.

Область линейной вязкоупругости ограничена таким интервалом амплитуд, в котором значение G*постоянно. В теории линейной вязкоупругости соответствующие уравнения являются линейными дифференциальными уравнениями и коэффициенты дифференциалов по времени являются постоянными, т.е. материальными константами. Выход за пределы области линейной вязкоупругости при использовании более высоких амплитуд и, следовательно, повышенных напряжений означает появление неучитываемых отклонений результатов измерений, связанных с выбором параметров испытаний и применяемой аппаратуры. При таких условиях образец деформируется до момента, когда физические связи между молекулами или агрегатами разрушаются, наступает сдвиговое разжижение, и большая часть вводимой энергии необратимо переходит в теплоту.

Нужно отметить следующее. Так как чрезвычайно важно определить область линейной вязкоупругости, любые динамические испытания неизвестных образцов необходимо начинать с развертки по амплитуде напряжения.