Измерение вязкоупругости.

Рассмотрим на примерах типичных вязкоупругих жидкостей вопрос о том, как лучше всего оценить в их реологическом поведении соотношение таких характеристик, как вязкость и упругость. Начнем с двух явлений, вызываемых упругостью, которые могут быть использованы для этого.

Эффект Вайссенберга

На рис. 5 было показано различие в поведении ньютоновской и вязкоупругой жидкостей при их перемешивании ротором в емкости. В то время как ньютоновская жидкость в результате действия центробежных сил отбрасывается наружу и вверх по стенкам стакана, вязкоупругая жидкость поднимается по валу ротора, преодолевая силу тяжести. Это явление можно увидеть во время перемешивания муки с водой при изготовлении теста.

Использованная выше модель вязкоупругой жидкости поможет нам понять причину подъема жидкости по валу ротора (рис. 28).

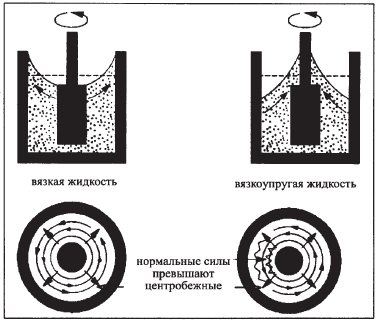
Рис. 28. Упругие молекулы, растянутые во внешних слоях, пытаются устремиться по направлению к низкоэнергетическому уровню

Постоянное вращение ротора создает в жидкости концентрические слои, линейная скорость которых повышается от внутренних слоев к наружным. В пределах этих слоев молекулы распутываются и ориентируются в направлении того слоя, в котором они находятся, и поскольку жидкость вязкоупругая, можно допустить, что молекулы во внешних слоях будут находиться в более растянутом состоянии, чем те, которые находятся ближе к ротору. Высокая степень растяжения также означает более высокое энергетическое состояние, из которого молекулы стремятся выйти. Имеется одна возможность выхода для таких растянутых молекул - это движение по направлению к оси ротора. Если все молекулы перемещаются к оси ротора, то здесь создается “теснота”, и остается только один путь выхода – вверх.

Таким образом, вращение обусловливает не только напряжение сдвига вдоль концентрических слоев, но также и дополнительное, нормальное напряжение, которое действует перпендикулярно вектору напряжения сдвига. Это нормальное напряжение заставляет вязкоупругие жидкости подниматься вверх по вращающимся валам и создает нормальную силу, стремящуюся разъединить конус и плоскость или две параллельные плоскости в ротационных реометрах.

Вязкоупругость жидкости, испытываемой в измерительной системе конус-плоскость, подобным же образом обусловливает нор­мальную силу, которая с увеличением скорости вращения извлекает жидкость из зазора и выталкивает ее на внешний обод конуса, в результате чего слой жидкого образца в измерительном зазоре расщепляется. На этом испытание следует прекратить, так как последующие измерения лишены физического смысла. Профессор Вайссенберг обнаружил это явление, обусловленное упругостью, которое впоследствии и было названо его именем.

Необходимость анализа упругого поведения многих жидкостей, таких как растворы полимеров или расплавы адгезивов, вызвала большой интерес к измерениям нормальных напряжений. Но при этом важно осознать одно обстоятельство, а именно: упругость, которую собираются измерить, неминуемо вызовет расщепление слоя образца, подвергаемого сдвигу в узле конус-плоскость. Это явление, называемое “эффектом Вайссенберга”, ограничивает применение измерительных узлов ротационных вискозиметров типа конус-плоскость и плоскость-плоскость для реологических испытаний, вязкоупругих жидкостей относительно низкими значениями скоростей сдвига, редко превышающими 100-200 с^-1. Скоростей сдвига, которые реализуются, например, при капиллярной реометрии, обычно не достигают.

Природа нормальных напряжений и разности нормальных напряжений.Сила, действующая на тело, деформирует его. При этом общее напряжение в любом кубическом элементе, выделенном в объеме этого тела, может быть разложено на девять компонент, как показано на рис. 29.

Для любой из граней куба можно определить нормальные на­пряжения, которые действуют перпендикулярно плоскости, и на­пряжения сдвига, которые действуют тангенциально.

Принято обозначать компоненты напряжения как t_ij, где первый индекс (i) относится к плоскости, на которую действует напряжение, а второй индекс (j) указывает направление компоненты напряжения.

Компоненту напряжения считают положительной, если она дей­ствует в направлении координатной оси. Все напряжения могут быть скомбинированы в тензор наряжений:

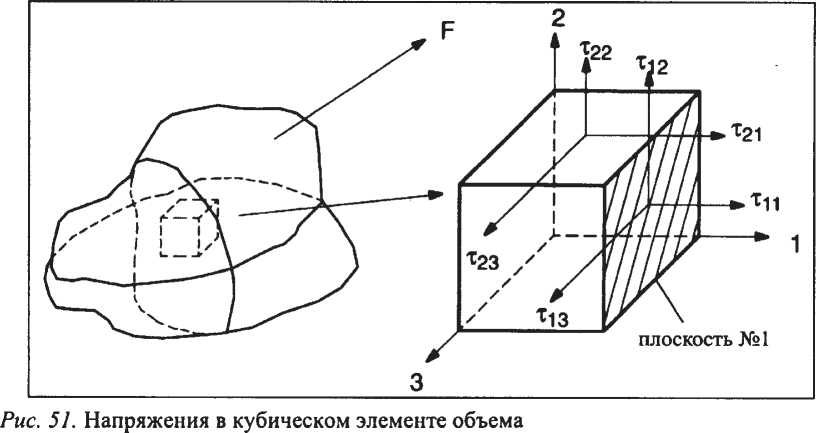
Рис. 29. Напряжения в кубическом элементе.

Данный тензор можно упростить:

а) 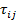= 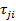, после чего остается в независимых компонент напряжения;

б) в случае несжимаемой жидкости абсолютные величины трех нормальных напряжений не влияют на ее деформацию. Деформация зависит только от разности между нормальными напряжениями и изотропным давлением или, что то же самое, от разности между тремя нормальными напряжениями.

Когда используют разность нормальных напряжений, то для полного описания влияния всех трех нормальных напряжений на деформацию необходимо учитывать только две разности.

В общем случае деформации несжимаемой жидкости напряженное состояние полностью описывается только тремя сдвиговыми напряжениями:

, ,

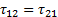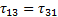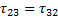
- и двумя разностями нормальных напряжений:

; .

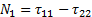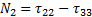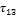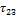В особом случае идеального сдвигового течения, к которому приближаются условия в измерительных системах типа ко­нус-плоскость, плоскость-плоскость, коаксиальных цилиндров, сдвиговая деформация прикладывается таким образом, что и равны нулю. В таком случае общее напряженное состояние в жид­кости описывается следующим образом: 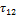— напряжение сдвига;

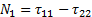- “первая разность нормальных напряжений”;

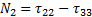- “вторая разность нормальных напряжений”

Для жидкости, проявляющей ньютоновский характер течения и первая и вторая разности нормальных напряжений равны нулю. Поэтому с реологической точки зрения такая жидкость при идеальном сдвиговом течении полностью описывается вязкостью ƞ = const.

Измерение сдвиговых и нормальных напряжений при средних скоростях сдвига в режиме установившегося течения характеризует образцы в области нелинейного вязкоупругого течения, т.е. в условиях, типичных для таких производственных процессов, как нанесение покрытий, распыление и экструзия. Для подобных процессов упругое поведение таких объектов, как расплавы или растворы высоко­молекулярных полимеров, часто более важно, чем вязкая реакция на сдвиг. Упругость часто является основным фактором, определяющим аномалии течения, которые ограничивают производительность или приводят к браку.