Тема 9. Метод ползучести-восстановления. Механические модели

В теории ползучести и восстановления и в ее математической трактовке модель испытуемого материала представляют в виде набора пружин или сочетания пружин с амортизаторами (вязкими демпферами) для того, чтобы получить корреляцию между приложенным напряжением и развивающейся во времени деформацией. Сравнение поведения реальных жидкостей с этими модельными системами и их свойствами позволяет обнаружить связи с молекулярной структурой жидкостей, например расплавов полимеров, и помогает понять природу вязкоупругости.

Чтобы понять, каким образом происходит развитие деформации во времени при приложении нагрузки к реальным вязкоупругим телам и жидкостям с очень сложной химической и физической структурой, необходимо сначала рассмотреть поведение очень простых модельных систем

Идеально твердое тело (рис. 31). После приложения к идеально твердому телу силы или напряжения следует мгновенная деформация, которая прямо пропорциональна приложенной силе. Так, удвоение на­пряжения означает удвоение деформации, которая остается постоянной до тех пор, пока действует это напряжение. Отношение деформации к напряжению есть мера упругости твердого тела. При снятии напряжения деформированные пружины мгновенно восстанавливают первоначальную форму. Взаимодействие сил и напряжений полностью обратимо. В качестве модели для характеристики идеально упругого тела обычно используют металлическую спиральную пружину, для которой сила и удлинение связаны линейно. Приложенные силы приводят к возникновению растягивающих или сдвиговых напряжений в образце, а модуль растяжения Е (модуль Юнга) или модуль сдвига G являются коэффициентами соответствующих уравнений, т. е. мерой сопротивления твердого тела деформации. Эти модули являются материальными константами данного твердого тела:

ϭ = Еγ; τ = Gγ,

где ϭ - растягивающее напряжение; τ - сдвиговое напряжение.

Как напряжения, так и деформации не зависят от времени.

Идеальная ньютоновская жидкость (рис. 32). Такая жидкость характеризуется линейной взаимосвязью приложенной силы и скорости деформации. Если к жидкости приложить только сдвиговые напряжения и поддерживать их постоянными, это приведет к линейному возрастанию деформации во времени. При снятии напряжения конечная деформация сохраняется. Для характеристики поведения ньютоновской жидкости используют модель амортизатора, или демпфера (движение поршня в цилиндре, наполненном маслом). Динамическая вязкость, характеризующая сопротивление жидкости силе, которая вызывает ее течение, есть присущий природе этой жидкости коэффициент пропорциональности в уравнении Ньютона:

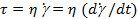
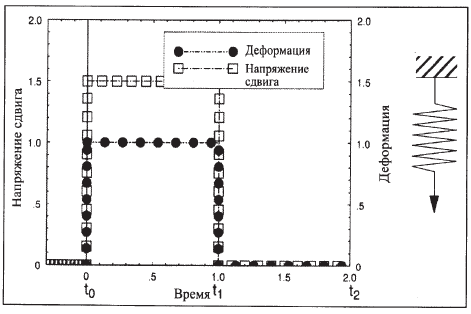
Рис. 31. Развитие напряжения сдвига и деформации во времени для идеального твердого тела.

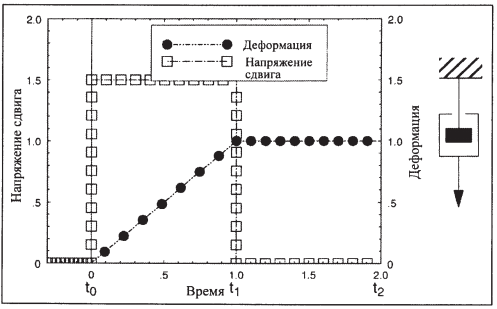
Рис. 32. Развитие напряжения сдвига и деформации во времени для идеальной жидкости

Комбинация пружин и демпферовдля описания вязкоупругости.Используя комбинации этих элементов модели, соединенных последовательно или параллельно, можно продемонстрировать типичные свойства вязкоупругих жидкостей или твердообразных тел и вывести математические уравнения для описания их реологического отклика. Комбинация демпфера и пружины позволяет моделировать зависимость реологических параметров от времени, что невозможно в случае модели, состоящей только из одного демпфера или одной пружины. Тип связей между механическими моделями определяется тем, имеем ли мы дело с вязкоупругим твердым телом (тело Кельвина-Фойхта) или вязкоупругой жидкостью (жидкость Максвелла). Эти модели относительно просты, поскольку они связывают только один демпфер с одной пружиной. Для обеих моделей, удовлетворяющих требованиям линейной вязкоупругости, предложены соответствующие уравнения. Реальные вязкоупругие вещества представлены более сложными комбинациями пружин и демпферов.

Модель Кельвина-Фойхта (рис. 33). Модель представляет собой комбинацию спирали и демпфера, соединенных параллельно. Жесткая рамка обеспечивает одинаковое воздействие на пружину и демпфер любой приложенной к этой системе силы.

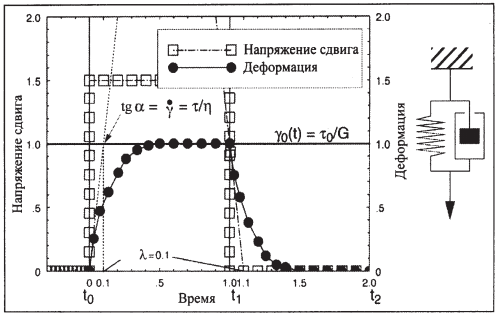
Рис. 33. Ползучесть и восстановление во времени (твердое тело Кельвина-Фойхта).

Эта система гарантирует, что общая деформация γ равна деформации демпфера 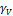и деформации пружины .

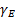Приложенное напряжение 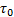равно сумме напряжений на демпфере 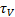и на пружине 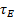. Подставляя в уравнение состояния величины упругой реакции пружины и вязкой реакции ньютоновской жидкости, получим

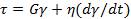
Решение этого дифференциального уравнения при постоянном напряжении имеет вид

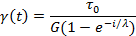
где λ - время запаздывания: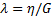

При снятии напряжения восстановление деформации “запазды­вает”.

Когда время tприближается к бесконечности, это уравнение сводится к виду

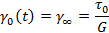
Это конечная реакция пружины. В начальный момент нагружения она тормозится демпфером.

При приложении напряжения деформация системы возрастает во времени, и начальный наклон кривой γ(t) связан со скоростью сдвига в демпфере ( 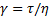). Время запаздывания λ равно времени, при котором 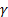= 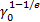. Это составляет примерно 67% конечной деформации. Графически λ определяется как точка пересечения касательной к начальному участку кривой деформации с линией, параллельной оси абсцисс при = .

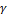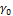При снятии напряжения на той стадии, когда деформация достигла стационарного уровня, модель Кельвина-Фойхта обратимо восстанавливается – деформация снижается до нуля согласно уравнению

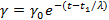
При времени t=t₂ деформация снижается до нуля, т.е. твердо­образный образец полностью восстанавливает свою первоначальную форму. Времена запаздывания λ в фазах ползучести и восстановления равны, если соблюдаются условия линейной вязкоупругости.

Под идеально твердым телом понимают такое тело, элементы объема которого не меняют своего положения необратимо, т. е. приложенное напряжение не приводит к какому-либо течению. Модель Кельвина-Фойхта описывает вязкоупругое твердообразное тело.

Модель Максвелла (рис. 34). В этой модели пружина и демпфер расположены последовательно, в результате чего напряжения сдвига в обоих элементах всегда равны, а деформации аддитивны:

=

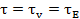
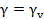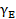
Производная по деформации имеет вид

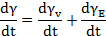
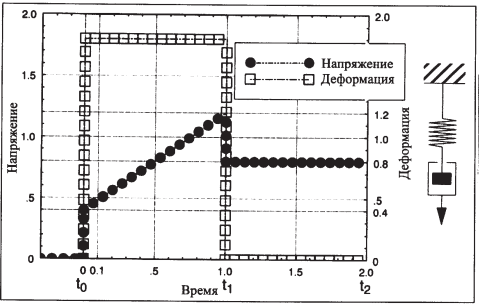
Рис. 34. Ползучесть и восстановление во времени (жидкость Максвелла).

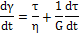
Это дифференциальное уравнение имеет следующее решение:

γ

Модель Максвелла характеризует вязкоупругую жидкость. При мгно­венном скачкообразном увеличении силы (напряжения) сначала на­блюдается мгновенная скачкообразная деформация системы, которая возрастает в соответствии с упругой реакцией пружины. Затем, на более поздней фазе испытания, система проявляет вязкую реакцию, т.е. деформация не прекращается до тех пор, пока действует приложенное напряжение; она продолжает возрастать с постоянной скоростью, обусловленной вязкостью жидкости в демпфере.

При мгновенном снятии напряжения в момент времени t₁ деформация моментально снижается, принимая новое, не зависящее от времени, значение. Этот спад деформации связан с освобождением пружины, тогда как остаточная постоянная деформация эквивалентна необратимой деформации (деформации течения) во время фазы ползучести.

Модель Бюргера (рис. 35). Две предыдущие модели – вязкоупругого твердообразного тела и вязкоупругой жидкости – слишком просты для того, чтобы попытаться представить с помощью любой из них поведение реального вязкоупругого материала. Гораздо лучше описывает поведение реального материала модель Бюргера, которая представляет собой комбинацию моделей Кельвина-Фойхта и Максвелла, соединенных последовательно.

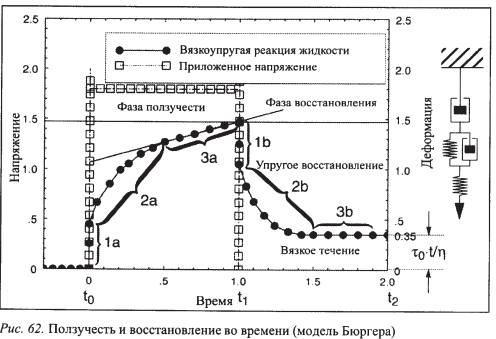
Рис. 35. Модель Бюргера.

Эта модель состоит из двух пружин с модулями G₀ и G₁ и двух демпферов с вязкостями 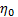и .

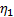Уравнения состояния этих двух последовательно расположенных элементов модели Бюргера имеют вид

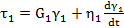(тело Кельвина-Фойхта)

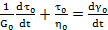(жидкость Максвелла)

Так как эти элементы соединены последовательно, напряжения каждого равны общему напряжению, а общая деформация равна сумме деформаций обоих элементов:

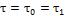
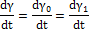
что может быть представлено в виде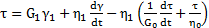

Полный математический расчет модели Бюргера приводит к сложному дифференциальному уравнению, которое может быть решено для фазы ползучести:

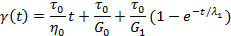
На рис. 32 показано развитие деформации в модели Бюргера при действии напряжения в фазе ползучести, для которой характерны три различные стадии изменения деформации:

1а – мгновенный скачок деформации в результате растяжения пружины Максвелла ;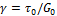

2а – медленное возрастание деформации, связанное с элементом Кельвина-Фойхта, который при t, приближающемся к бесконечности, достигает равновесной величины ;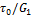

3а – чисто вязкая реакция модели Бюргера, связанная с демпфером элемента Максвелла, который начинает работать после того, как элемент Кельвина-Фойхта достигнет равновесного состояния; после этого наклон кривой деформация - время становится постоянным и равным скорости сдвига: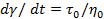

Экстраполяция линейного участка этой кривой до пересечения с осью ординат дает величину “установившейся” деформации у(0), которую определяют как

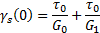
т. е. она равна упругости двух пружин с модулям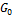и и .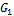

При снятии напряжения 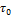модель Бюргера восстанавливается ступенчато:

1 б- при t= 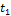деформация снижается мгновенно благодаря реакции пружины ;

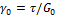после этого следуют две стадии, зависящие от времени:

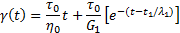
(где 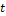> 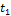), а именно:

3 б - член 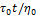равен постоянной пластической деформации и представляет вязкое течение демпфера Максвелла;

2 б - второй член уравнения экспоненциально снижается и при t =∞ достигает величины .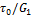

При испытании образца в пределах области линейной вязкоупругости элементы, которые обусловливают упругую реакцию, будут давать равный вклад в фазу ползучести и в фазу восстановления.