Давление газа. Абсолютная температура. Молекулярно-кинетическое обоснование абсолютной температуры и давления. Измерение давления и температуры.

Предмет молекулярной физики. Основные положения молекулярно-кинетической теории (МКТ) вещества и их экспериментальное обоснование. Статистический и термодинамический подходы к изучению макроскопических систем. Флуктуации и их проявления.

В данном разделе курса общей физики, в отличие от раздела "Механика", рассматриваются закономерности, присущие большому количеству частиц. Как мы увидим в дальнейшем, количественное увеличение числа частиц в системе обуславливает качественные изменения ее свойств. Молекулярная физика и термодинамика изучают поведение макросистем.

Макросистемой называется система, состоящая из очень большого числа частиц.

Область физики, в которой изучаются физические свойства тел в различных агрегатных состояниях на основе рассмотрения их микроскопического (молекулярного) строения, называется молекулярной физикой.

В этом разделе физики рассматриваются строение и свойства газов, жидкостей и твердых тел, изменения, которые в них происходят при изменении внешних условий, фазовые превращения, явления переноса и др.

Молекулярно-кинетической теорией вещества называется учение, которое объясняет строение и свойства тел движением и взаимодействием атомов и молекул, из которых состоят тела.

Основоположником молекулярно-кинетической теории (МКТ) является М.В. Ломоносов (1711-1765 г.г.), который сформулировал ее основные положения и применил их к объяснению различных явлений.

Основные положения МКТ заключаются в следующем:

1. Все тела в природе состоят из мельчайших частиц (атомов и молекул), в состав которых входят более мелкие элементарные частицы;

2. Эти частицы находятся в непрерывном хаотическом движении, которое называется тепловым движением;

3. Между частицами вещества действуют силы притяжения и отталкивания, зависящие от расстояния между частицами.

Рассмотрим явления экспериментально подтверждающие МКТ:

1. Наличие молекул подтверждается возможностью механического дробления вещества, растворением веществ в воде и других растворителях. Очевидно, что при дроблении вещества можно получить очень маленькие частички. Наименьшая, электрически нейтральная частица вещества, сохраняющая все его химические свойства, называется молекулой. Молекулы складываются из более простых частичек – атомов. Атомом называют наименьшую частицу данного химического элемента.

Существует очень много молекул (~7000000), в то время как число атомов небольшое. В настоящее время известно 113 разных атомов. В природе существует 88 атомов, 25 получены искусственно с помощью ядерных реакций. Эти 113 атомов называются химическими элементами. Атомы химических элементов, комбинируясь друг с другом, создают миллионы существующих молекул.

2. Диффузия – самопроизвольное взаимное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей или твердых тел. Наиболее интенсивно она протекает в газах и менее интенсивно в жидкостях и твердых телах, особенно при низких температурах. Явление диффузии свидетельствует о том, что между молекулами газов, жидкостей и твердых тел есть промежутки, т.е. вещество дискретно.

Рис.1. Легкие молекулы диффундируют быстрее тяжелых

3. Смешивание разных жидкостей, растворение твердых тел в жидкостях объясняется перемешиванием молекул разного рода. При этом объем смеси может отличаться от суммарного объема компонентов смеси, что свидетельствует о разной компактности молекулярных систем:

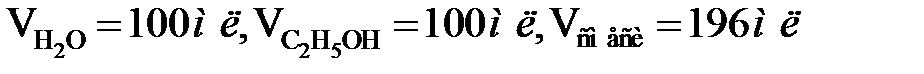
4. Газ занимает любой предоставленный ему объем. Это значит, что молекулы газа двигаются независимо одна от другой, хаотично, беспрерывно. При этом движение молекул в любом направлении равновероятно. Это очевидно, потому что давление газа в закрытом сосуде одинаковое во всех точках объема.

5. Наиболее ярким экспериментальным подтверждением представлений МКТ о беспорядочном движении атомов и молекул является броуновское движение. Это тепловое движение мельчайших микроскопических частиц, взвешенных в жидкости или газе. Явление впервые наблюдал ботаник Броун в 1827 г., рассматривая в микроскоп взвешенные в воде споры плауна. Скорость броуновской частицы беспорядочно меняется по модулю и направлению, а ее траектория представляет собой сложную зигзагообразную кривую (рис. 2.). Теория броуновского движения была создана А. Эйнштейном (1905 г.) и М Смолуховским (1906г.). Экспериментально теория Эйнштейна была подтверждена в опытах французского физика Ж. Перрена (1908–1911 гг.). Это способствовало превращению молекулярно-кинетической гипотезы в теорию.

Рис.2. Траектория броуновской частицы

Было установлено, что скорость броуновской частички увеличивается с увеличением температуры, с уменьшением вязкости жидкости и массы частички. Броуновские частички окружены молекулами жидкости, которые движутся беспрерывно и хаотично (тепловое движение). При размерах частичек порядка 10^-4 – 10^{-5 м число ударов молекул жидкости о них не будет слишком большим. В этом случае начинают проявляться отклонения числа ударов молекул в отдельные стороны частички от средних значений.}

Отклонение тех или иных величин от их средних значений, которые происходят в малых объемах или на протяжении малых промежутков времени, называются флуктуациями.

Флуктуации скорости молекул и числа ударов приводят к тому, что импульсы, которые получает броуновская частичка с разных сторон, оказываются некомпенсированными. Частичка перемещается, изменяя величину и направление скорости.

Также как и броуновское движение, ряд физических явлений обусловлен флуктуациями соответствующих величин, которые характеризуют это явление. Так флуктуациями плотности воздуха объясняется голубой цвет неба. В атмосфере, в малых объемах беспрерывно возникают сгущения и разряжения молекул воздуха, на которых рассеивается солнечный свет. Согласно закону Релея голубые и синие лучи рассеиваются сильнее, чем желтые и красные. Поэтому цвет неба голубой, а восходящее и заходящее солнце красное. Флуктуации плотности наблюдаются вблизи критического состояния вещества. На этих флуктуациях плотности происходит интенсивное рассеяние света, получившее название критическая опалесценция.

6. В любом, даже очень маленьком объеме вещества находится огромное число молекул. Так при нормальных условиях, (p=1,01*10⁵Па, Т=273К) в 1см³ воздуха находится n_o=2.69*10¹⁹ молекул – так называемое число Лошмидта.

В молекулярно-кинетической теории количество вещества принято считать пропорциональным числу частиц. Единица количества вещества называется молем (моль).

Моль – это количество вещества, содержащее столько же частиц (молекул, атомов), сколько атомов содержится в 0,012 кг изотопа углерода ₆C¹².

Таким образом, в одном моле любого вещества содержится одно и то же число частиц (молекул). Это число называется числом Авогадро N_A:

N_A = 6,02·10²³ моль^–1.

Число Авогадро – одна из важнейших постоянных в физике.

Количество вещества ν определяется как отношение числа N частиц (молекул) вещества к постоянной Авогадро N_A:

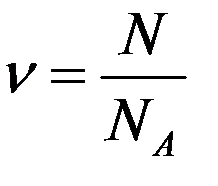
Массу одного моля вещества принято называть молярной массой μ. Молярная масса равна произведению массы m₀ одной молекулы данного вещества на число Авогадро:

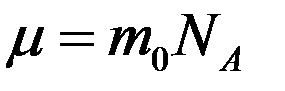
Молярная масса выражается в килограммах на моль (кг/моль). Для веществ, молекулы которых состоят из одного атома, часто используется термин атомная масса.

За единицу массы атомов и молекул принимается 1/12 массы атома изотопа углерода ₆C¹² (с массовым числом 12). Она называется атомной единицей массы (а. е. м.):

1 а. е. м. = 1,66·10^–27 кг.

Эта величина практически совпадает с массой протона или нейтрона.

Относительная атомная масса, или атомная масса химического элемента - это отношение массы атома этого элемента к 1/12 массы атома ₆C¹². Относительные атомные массы химических элементов приводятся в таблице Менделеева.

Относительная молекулярная масса вещества - это отношение массы молекулы этого вещества к 1/12 массы атома углерода ₆C¹². Зная химическую формулу вещества можно найти молекулярную массу как сумму атомных масс элементов, составляющих данное вещество. Например, у воды химическая формула H₂O, атомная масса водорода равна 1, умножаем ее на 2 и прибавляем атомную массу кислорода, 16, получаем, что молекулярная масса воды равна 18. Это безразмерное число, т. к. речь идет об относительной молекулярной массе.

Можно говорить и просто о массе атома, о массе молекулы, которые измеряют обычно в атомных единицах массы (а.е.м.). Таким образом, масса молекулы воды равна 18 а.е.м. Из определения моля следует, что молярная масса μ, выраженная в граммах, численно равна относительной молекулярной массе. Так масса одного моля воды равна 18 г.

Количество вещества (число молей) может быть рассчитано по формуле:

,

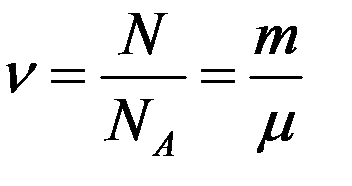где N — число молекул в веществе массой m.

7. В конце XIX века были получены фотографии отдельных молекул и атомов Выполненные с помощью туннельного электронного микроскопа.

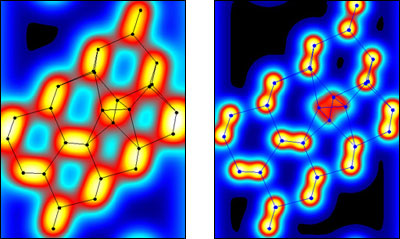
На рисунке слева: дефект в кристалле при разрешении в 2 ангстрема(0.2 нм). На рисунке справа - то же, но при разрешении в 1 ангстрем.

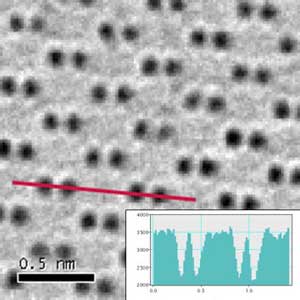
Фото атомов германия на сапфировой подложке:

Сегодня многие связывают рождение новой эпохи с 1981 годом, когда немецкие физики Герд Бинниг и Генрих Рорер создали зондовый туннельный микроскоп, позволяющий не только видеть, но и переносить с места на место отдельные атомы. Но порой нужны годы, чтобы научный прибор стал инструментом технолога. Только в 1989 году сканирующий туннельный микроскоп удалось использовать как наноманипулятор, сложив с его помощью регулярную структуру из атомов. Сотрудниики IBM Дональд Эйглер и Эрхард Швейцер выложили название своей компании 35 атомами ксенона на поверхности кристалла никеля. Эта операция заняла 22 часа и проходила при температуре вблизи абсолютного нуля (–273°С). После нагрева кристалла до –230°С буквы IBM испарились.

8. Упругость газов, очень малая сжимаемость жидкостей и твердых тел подтверждают наличие сил отталкивания между молекулами. Сохранение твердыми телами формы, необходимость приложения силы для отрыва тел от поверхности жидкости свидетельствуют о наличии сил притяжения между молекулами. На расстояниях порядка ~10^-9м между молекулами начинают действовать силы притяжения. Эти силы короткодействующие, они быстро уменьшаются с увеличением расстояния r между молекулами по закону:

,

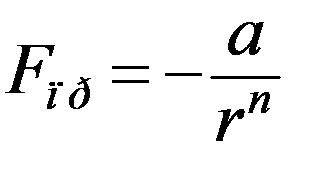где – a коэффициент, зависящий от строения молекул, n ≈ 7.

На расстояниях r между центрами молекул порядка ~10^-10м заметно начинают действовать силы отталкивания, которые изменяются по закону:

,

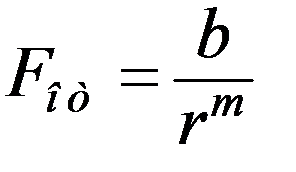где – m ≥ 9.

Очевидно, что силы отталкивания изменяются с расстоянием быстрее, чем силы притяжения. При некотором r = r_о силы притяжения уравновешивают силы отталкивания, и их равнодействующая становится равной нулю:

.

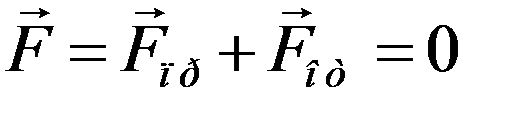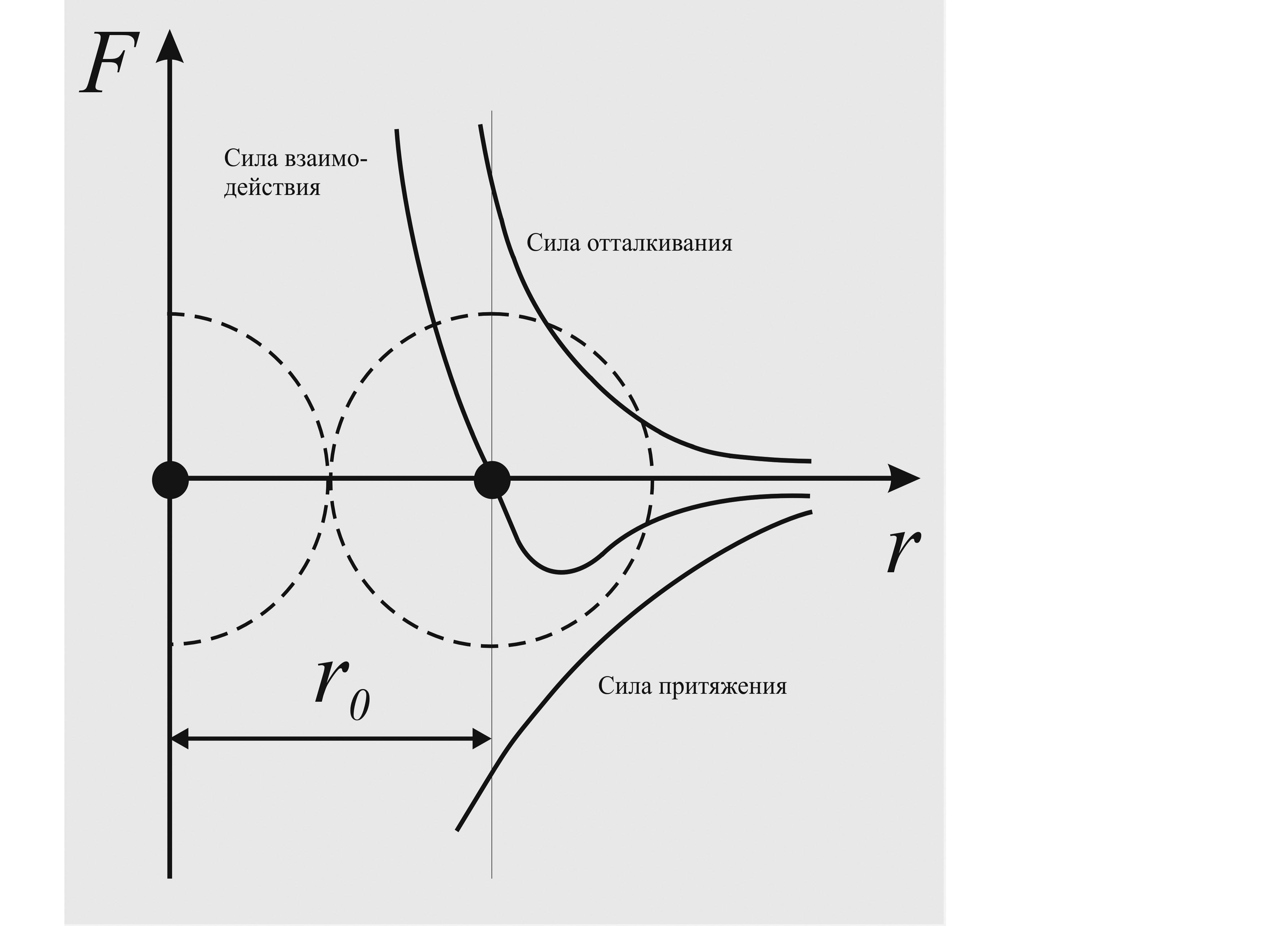
Рис.3.Сила взаимодействия (равнодействующая) F, силы притяжения и отталкивания двух молекул. F > 0 – преобладают силы отталкивания, F < 0 – преобладают силы притяжения.

Таким образом, наиболее устойчиво молекулы размещаются на некотором минимальном расстоянии r_o. Это расстояние условно можно принять за диаметр молекулы. Потенциальная энергия взаимодействия при r = r_o минимальна. Если расстояние между молекулами достаточно велико, то преобладают силы межмолекулярного притяжения. На малых расстояниях преобладают силы отталкивания.

Число атомов и молекул в любом теле огромно. Например, в 1 м³ газа при обычных условиях содержится ~10²⁵ молекул, а в жидких и твердых телах ~10²⁸ молекул. Если считать, что движение каждого атома или молекулы подчиняется законам классической механики, то практически даже невозможно написать систему дифференциальных уравнений движения такого множества молекул (бумаги на Земле для этого не хватило бы) и решить эту систему. Поэтому поведение отдельной молекулы или атома тела не может быть изучено методами классической механики, тем более что это поведение (траектория, скорость и другие характеристики движения молекулы) изменяются со временем случайным образом.

Физические свойства макроскопических систем, состоящих из большого числа частиц, изучаются двумя взаимно дополняющими методами: статистическим и термодинамическим.

Статистический метод основан на использовании теории вероятностей и определенных моделей строения изучаемых систем. В совокупном поведении большого числа частиц, координаты и импульсы которых случайны в любой момент времени, проявляются особые статистические закономерности. Статистический метод истолковывает физические свойства макросистем, непосредственно наблюдаемые на опыте (давление, температура и т.д.) как суммарный, усредненный результат действия отдельных частиц. Например, в газах можно определить средние значения скоростей молекул и их энергий, однозначно связанных с температурой. Раздел физики, который изучает физические свойства макроскопических систем с помощью статистического метода, называется статистической физикой. Статистическая физика базируется на основных положениях молекулярно кинетической теории и изучает те параметры систем (давление, температура и т.д.), которые наблюдаются на опыте.

Термодинамика изучает свойства макроскопических систем и протекающие в них процессы, не вдаваясь в микроскопическую природу тел. Не рассматривая поведение отдельных микроскопических частиц, термодинамика позволяет сделать ряд выводов относительно протекания процессов в макросистеме, оперируя некими интегральными понятиями - параметрами (давление, температура, объем) и функциями состояния (внутренняя энергия и энтропия и др.).

Термодинамический метод основан на анализе условий и количественных соотношений, возникающих в системе при различных превращениях энергии. Соотношения между разными видами энергии позволяют изучать физические свойства исследуемых систем при самых разнообразных процессах и предсказать направления изменения состояния макросистем.

В основе термодинамики лежат несколько фундаментальных законов, называемых началами термодинамики, которые были установлены путем обобщения большого количества опытных фактов.

У статистической физики и термодинамики общий предмет изучения - свойства макросистем (веществ) и происходящие в них процессы. Подходя к изучению этих свойств и процессов с различных точек зрения, статистическая физика и термодинамика взаимно дополняют друг друга, образуя, по существу, единое целое.

Лекция 2

Давление газа. Абсолютная температура. Молекулярно-кинетическое обоснование абсолютной температуры и давления. Измерение давления и температуры.

Газ, который находится в сосуде, оказывает давление на его стенки и тела находящиеся в нем. Именно своим давлением газ и обнаруживает свое присутствие. Давление газа можно объяснить на основе молекулярно кинетической теории. Так при каждом ударе молекула действует на стенку с некоторой силой. Когда число молекул очень велико, то очень большим будет и число ударов о стенки. Очень малые силы отдельных ударов складываются в конечную, практически постоянную силу, которая действует на стенки.

Сила, действующая на единицу площади поверхности, и будет давлением, которое и создает газ. По определению:

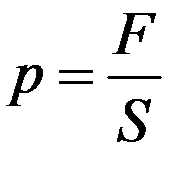
где F – сила, которая действует со стороны молекул на площадку S сосуда с газом.

ЕДИНИЦЫ ИЗМЕРЕНИЯ ДАВЛЕНИЯ.

1. Система СИ: паскаль (Па) [1 Па = 1 Н/м²]

2. Внесистемные единицы:

1 (нормальная, физическая) атмосфера. (атм.) = 760 мм ртутного столба (мм.рт.ст.) (при t = 0оС) = 1,01·10⁵ Па = 1,01 бар.

1 бар = 10⁵ Па

1 мм. рт. ст. = 1,00000014 Торр = 133,3 Па

Диапазон давлений, которые приходится измерять на практике, очень велик – от 10^-14Па до 10⁺¹²Па.

Не существует устройств, которые одновременно точно измеряли бы такие низкие и высокие давления. Поэтому приборы для измерения давления подразделяются на вакуумметры – устройства для измерения давлений ниже атмосферного, барометры – для измерения атмосферных давлений и сравнимых с ними и манометры – для измерения высоких и сверхвысоких давлений.

Простейшим манометром для измерения давлений больших и меньших атмосферного служит открытый жидкостный манометр – U – образный сосуд с жидкостью (рис.1):

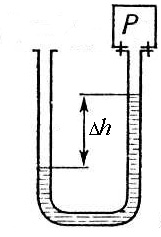
Рис.1 Жидкостный манометр

Одно из колен соединяют с сосудом, где измеряется давление, второе соединяется с атмосферой. При разности уровней жидкости в коленах манометра Δh давление в сосуде можно рассчитать по формуле:

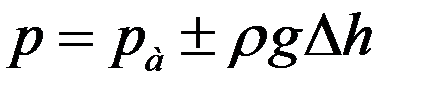
где p_а – атмосферное давление, ρ – плотность жидкости.

Если манометр заполнить водой, либо более легкой жидкостью, то им можно измерять малые разности давлений: 1-10³ Па. При заполнении манометра ртутью можно измерять давления сравнимые с атмосферным.

Для измерения высоких давлений (до ~ 10⁹Па) используются механические манометры с упругими элементами (манометры Бурдона) (рис.2). Главная его часть металлическая трубка, имеющая форму витка (B). Один конец трубки присоединен к корпусу прибора и соединен с сосудом, в котором измеряется давление. Другой, закрытый конец трубки соединен со стрелкой прибора. При увеличении давления виток распрямляется и перемещает стрелку вдоль шкалы. Прибор предварительно градуируется.

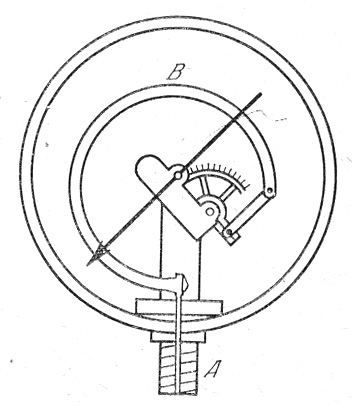
Рис.2 Манометр Бурдона

Для измерения малых давлений используются манометры Мак-Леода, Пирани, ионизационные и др.

Другой макроскопической величиной, характеризующей состояние системы, является температура. Под температурой понимают величину, которая характеризует тепловое состояние системы (тела). Она определяет, будет ли эта система предавать тепло другой системе с другой температурой, либо получать от нее тепло.

Своеобразность температуры как физической величины в том, что она в отличие от многих других величин не аддитивная. Это значит, что если мысленно разбить систему (тело) на части, то температура системы не будет равна сумме температур ее частей. Этим она отличается от других физических величин, таких как масса, объем и т.д. Поэтому температуру тела (системы) нельзя измерить непосредственно, т.е. методом сравнения с эталоном.

Для измерения температуры пользуются тем, что при изменении температуры тела изменяются его физические свойства: длина, объем, плотность электропроводность и т.д.

Для создания устройства для измерения температуры (термометр) выбирают какое-нибудь вещество – так называемое термометрическое вещество и определенную величину, характеризующую свойства тела – термометрическую величину. Выбор одного и второго абсолютно произвольный. Например, в технике и в быту широко используется ртутный термометр, где термометрической величиной является ртуть, а термометрической величиной – длина ртутного столба.

Для получения температурной шкалы выбирают реперные точки, установленные международным соглашением. Например, температура плавления льда и температура кипения воды. Полученный промежуток делят на 100 равных частей (шкала Цельсия). Одна часть называется градусом Цельсия. Пользуясь этим способом можно получить множество температурных шкал: разные термометрические вещества – разные шкалы.

Современная термометрия базируется на шкале идеального газа, которая устанавливается с помощью газового термометра (рис.3).

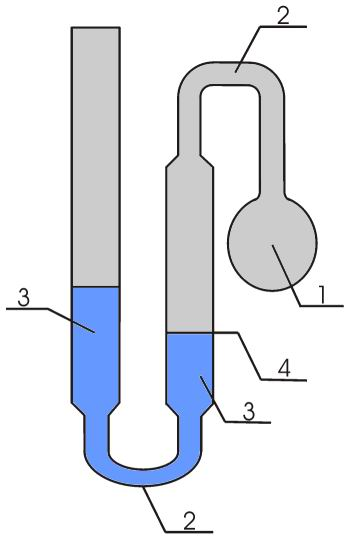
Рис. 3. Газовый термометр постоянного объема

1 - сосуд с газом, 2 - соединительные трубки,

3- манометр, 4 - постоянный уровень

Газовый термометр представляет собой закрытый сосуд, заполненный идеальным газом и снабженный манометром. Термометрическим веществом является идеальный газ, термометрической величиной – давление газа при постоянном объеме. Постоянство объёма достигается тем, что вертикальным перемещением левой трубки уровень в правой трубке манометра доводится до одного и того же значения (опорной метки) и в этот момент производится измерения разности высот уровней жидкости в манометре. Учет различных поправок (например, теплового расширения стеклянных деталей термометра, адсорбции газа и т.д.) позволяет достичь точности измерения температуры газовым термометром постоянного объема, равной одной тысячной кельвина.

Зависимость давления газа от температуры линейная. Следовательно, отношение давлений при температуре кипения воды p_к и таяния льда p₀ равно отношению этих температур:

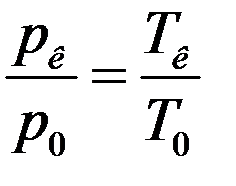
Отношение p_к/p₀ находится опытным путем:

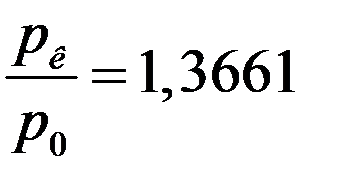
Следовательно:

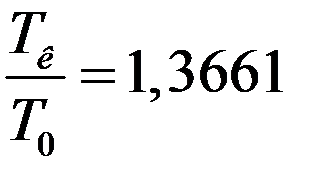(1)

Единица измерения температуры находится делением разности T_к – T₀ на 100 частей и называется Кельвином:

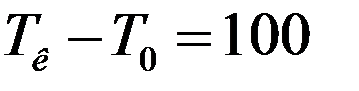(2)

Из равенств (1) и (2) получаем, что температура таяния льда по этой шкале равна:

,

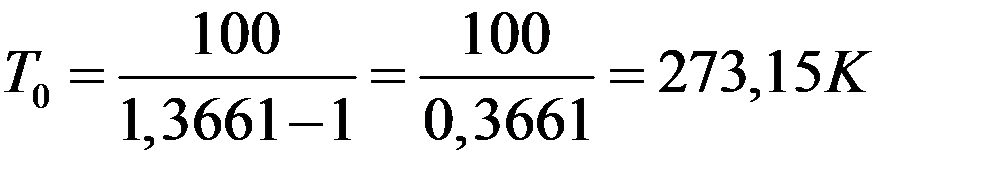а температура кипения воды T_к = 373,15K.

При определении температуры тела с помощью газового термометра, необходимо привести это тело в контакт с газовым термометром, дождаться теплового равновесия, затем измерить давление p в термометре. Температура тела определяется из соотношения:

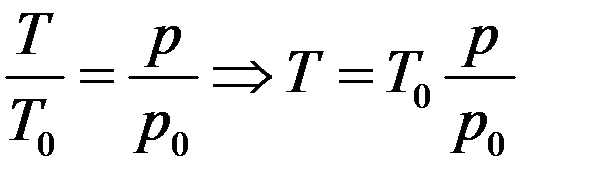(3)

где p₀ – давление газа при температуре таяния льда T₀.

Пользоваться газовым термометром не совсем удобно. У газовых термометров другое назначение. Их используют при градуировке других термометров, используемых на практике.

Температура, которая равна нулю по этой шкале – это температура, при которой давление идеального газа равно нулю (3).

Если при нуле температурной шкалы термометрическая величина обращается в нуль, то такая шкала называется абсолютной шкалой.

Температура, которая отсчитывается по такой шкале, называется абсолютной температурой. Рассмотренная шкала называется шкалой Кельвина.

Температура одна из основных величин в системе CI, а единица температуры – Кельвин – одна из основных единиц этой системы.

В международной системе единиц принята термодинамическая шкала температур, которая не зависит от свойств термометрического вещества. За нулевую температуру принята температура, при которой давление идеального газа равно нулю.

Это самая низкая из всех возможных температур. Поэтому на абсолютной шкале температур отрицательных температур не существует. Достигнуть абсолютного нуля невозможно, к нему можно только приблизиться. В настоящее время получены температуры порядка ~10^-6K.

За вторую реперную точку принята температура тройной точки воды. Тройная точка воды это температура, при которой вода, ее пар и лед находятся в динамическом равновесии. По шкале Цельсия она равна 0,01^оС. Температуру тройной точки воды по термодинамической шкале температур приняли равной точно 273,16 K. Выбор такого численного значения температуры тройной точки воды сделан для того, чтобы 1K был точно равен 1^оС.

Таким образом, 1K равен 1/273,16 части температурного интервала от абсолютного нуля температуры до температуры тройной точки воды.

Так как температура тройной точки воды по международной шкале термодинамической шкале температур T_т = 273,16K, а по шкале Цельсия t_т = 0,01^оС и 1^оС = 1K, то соотношение между температурами этих шкал имеет вид:

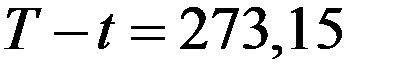
Отсюда следует:

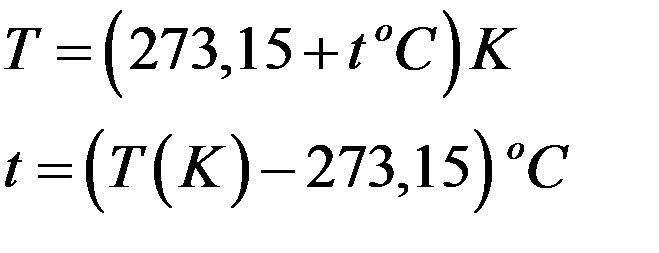
Для измерения температуры наибольшее распространение получили жидкостные термометры, термометры сопротивления и термопары.

В жидкостном термометре термометрическим веществом является ртуть, спирт, толуол, пентан и т.д. Диапазон измерения температуры жидкостными термометрами от -125^оС до +900^оС.

Жидкостные термометры бывают разного назначения: обычные термометры, максимальные и минимальные термометры, контактные термометры. Максимальные и минимальные термометры – приборы, показывающие максимальную и минимальную температуру в течение определенного промежутка времени.

В термометрах сопротивления термометрическим веществом является металл или полупроводник, сопротивление которых изменяется с изменением температуры. Изменение сопротивления измеряется с помощью мостовых схем. Диапазон измерения температуры 4 – 1300 K.

В термопарах чувствительными элементами являются спаи двух металлов A и B (рис.4).

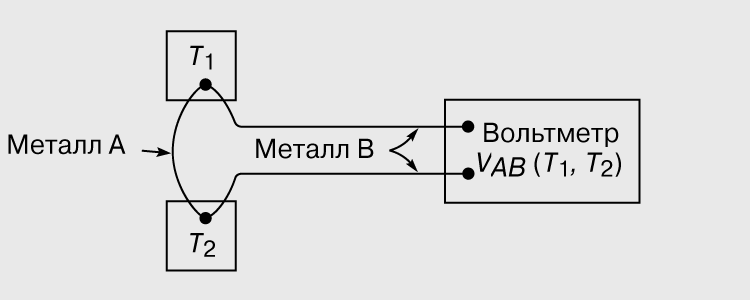
Рис.4 Схема включения термопары

Один спай должен находиться в тепловом равновесии с телом, температура которого измеряется, другой при известной постоянной температуре (чаще всего при температуре таяния льда). Если спаи находятся при разной температуре, то в такой цепи возникает так называемая термоэлектродвижущая сила (термо - ЭДС), которая измеряется микровольтметром, или гальванометром. Величина термо ЭДС пропорциональна разности температур спаев. Диапазон измерения температур -200 – 2200^оС.

Для измерения очень высоких температур используют радиационные пирометры. Они измеряют энергию, которую излучают нагретые тела. Эта энергия связана с температурой тела законом Стефана – Больцмана.

Лекция 3