Коробки скоростей с бесступенчатым регулированием

Для бесступенчатого регулирования скорости в основном применяют двигатели постоянного тока с тиристорной системой управления. Эти двигатели все шире используют в станках с ЧПУ, а также в многооперационных станках с ЧПУ и АСИ [10, 11].

В таких двигателях диапазон регулирования скорости с постоянной мощностью находится в пределах R_б = (R_д)_p = 2,5-6 (иногда до 8-10), что не перекрывает всего требуемого диапазона регулирования на шпинделе с постоянной мощностью R_р. Частоты вращения при постоянном моменте (R_д)_м регулируют в очень широком диапазоне. Перспективным является применение бесколлекторных электродвигателей постоянного тока, что повышает их надежность.

В приводе главного движения используют и регулируемые за счет изменения частоты тока асинхронные электродвигатели, у которых

,

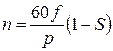где f – частота тока; р – число пар полюсов; S – скольжение. Эти двигатели обладают высокой надежностью, жесткой характеристикой и обеспечивают регулирование с постоянной мощностью во всем диапазоне.

Так как диапазон бесступенчатого регулирования R_б механических вариаторов или диапазон (R_д)_p регулируемых двигателей значительно меньше требуемого диапазона регулирования частот вращения шпинделя R_n или R_p при системах комбинированного регулирования, между устройством для бесступенчатого регулирования и шпинделем вводят обычно ступенчатую коробку. При этом должно выполняться условие

R_n = R_б R_к,

где R_к – диапазон регулирования коробки скоростей, т.е. коробку скоростей можно рассматривать как переборную группу, расширяющую диапазон регулирования привода, и можно записать

φ_к = R_к-1φ = R_б φ.

С учетом того, что при бесступенчатом регулировании φ ® 1, необходимо, чтобы φ_к = R_d. Следовательно,

,

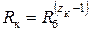окончательно

,

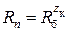что позволяет определить число ступеней коробки скоростей

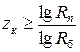или .

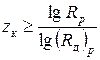Вследствие переменного скольжения в электродвигателях, механических вариаторах, ременных передачах фактический диапазон регулирования бесступенчатого устройства может оказаться меньше R_d, поэтому во избежание разрыва бесступенчатого ряда оборотов на шпинделе принимают обычно φ_к = (0,94…0,97)R_б.

Если коробка скоростей выполнена в виде одной группы передач, то для привода без перекрытия при z_к = 2 можно обеспечить диапазон регулирования 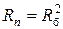, если R_б < 8; при z_к = 3 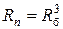, если 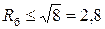(если R_б > 2,8, то в приводе получается перекрытие скоростей и ).

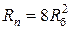Привод с z_к = 4 = 2₀ · 2₁ позволяет получить 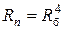, если R_б < 2,8 (при R_б > 2,8 получается перекрытие и ).

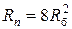При вычислении z_к и округлении его значения в бóльшую сторону перекрытие скоростей получается автоматически. В качестве примера на рис. 3.4 изображены кинематическая схема, график частот вращения и диаграмма мощности привода с z_к = 3 при .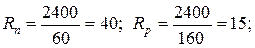

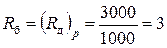В приводе получается перекрытие скоростей, так как 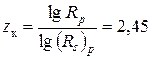округлено в большую сторону до z_к = 3.

В многооперационных станках с числовым управлением иногда сокращают число ступеней скорости, округляя z_к в меньшую сторону, что приводит к небольшому разрыву в средней части диапазона регулирования.

Если применен двигатель постоянного тока с двухзонным регулированием, то в этом интервале возможно регулирование частоты при постоянном моменте. На рис. 3.5 приведены график частот вращения и диаграмма мощности привода, построенного для предыдущего примера при z_к = 2. Такой прием упрощает механическую часть привода, однако, он возможен, если технологические операции, осуществляемые в средней части диапазона, не требуют полной мощности, либо их возможно осуществить на заниженных режимах обработки без существенного снижения производительности.

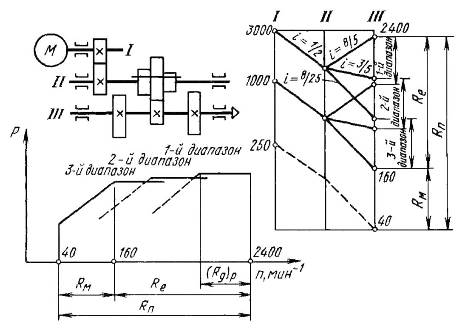
Рис. 3.4. Привод главного движения станка с регулируемым двигателем:

а – кинематическая схема; б – график частот вращения; в – диаграмма мощности

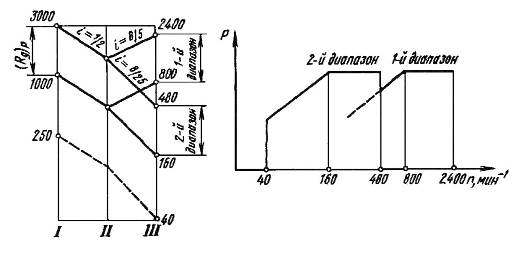
Рис. 3.5. Привод главного движения станка с регулируемым двигателем

при уменьшенном числе передач в коробке (z_к = 2):

а – график частот вращения; б – диаграмма мощности

Следует учитывать, что в станках с числовым управлением при применении двигателей постоянного тока регулирование скоростей часто ведется не бесступенчато, а ступенчато с малым φ (обычно φ = 1,12, реже φ = 1,06). В этом случае упрощается управление приводом, а потеря экономически выгодной скорости незначительна. Широко применяют структуры с перебором, позволяющие расширить общий диапазон регулирования и получить другие преимущества, свойственные этой структуре.

На рис. 3.6 изображен график частот вращения привода главного движения многооперационного станка.

3.4.3. Коробки скоростей

со сложенной структурой

Обычная множительная структура, состоящая из одной кинематической цепи с последовательным соединением групп передач, является наиболее простой. Она позволяет создавать рациональные приводы главного движения. Однако во многих случаях, особенно при увеличении диапазона регулирования скоростей, создать простой привод, удовлетворяющий требованиям, на базе обычной структуры невозможно. Поэтому в практике станкостроения применяют так называемые сложенные структуры – структуры многоскоростного привода, состоящие из двух или более кинематических цепей, каждая из которых является обычной множительной структурой. Одна из этих цепей (короткая) предназначена для высоких скоростей привода, другие (более длинные) – для низких скоростей [6].

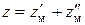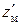Множительные структуры состоят чаще всего из двух, реже из трех кинематических цепей. Общее число скоростей привода для структуры, состоящей из двух цепей, , где и 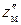– число ступеней первой и второй кинематических цепей. Если цепи имеют одинаковые группы передач (по количеству и характеристике), то их можно объединить в общую цепь. Пусть z_о – число скоростей общих передач, 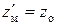, а 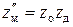; тогда 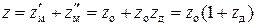. Общую часть структуры z_о, используемую для получения всех скоростей, называют основной, z_д – дополнительной.

Для объединения составляющих структур в одну – сложенную в схему привода – вводят соединительные передачи. Наиболее распространенные принципиальные схемы соединения двух структур представлены на рис. 3.7.

Верхнюю область регулирования скоростей вращения шпинделя получают при помощи основной структуры z_о и передают движение на шпиндель I через зубчатую передачу 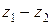(рис. 3.7, а) или через муфту 1 (рис. 3.7, б). Нижнюю область регулирования обеспечивают последовательным соединением основной z_о и дополнительной z_д структур соединительной передачей (на схеме показано условно).

б)

а) в)

Рис. 3.7. Схемы соединения множительных структур

На рис. 3.8 показана простая схема коробки скоростей со сложенной структурой. Здесь сложены две кинематические цепи, структуры которых: 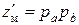и 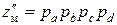. Группы колес р_a и р_b являются общими и поэтому образуют основную структуру 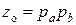; они вращают полый вал III. Далее движение шпинделю V от первой цепи передается с помощью муфты, а от второй цепи – через звено возврата (перебор) с колесам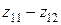и и 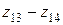, которые играют роль соединительных передач. Общее число скоростей привода

.

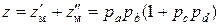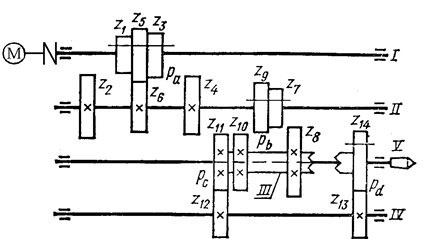
Рис. 3.8. Схема коробки скоростей со сложенной структурой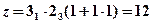

Для нашего случая р_a = 3₁; р_b = 2₃ и р_с = р_d = 1. Поэтому .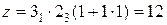

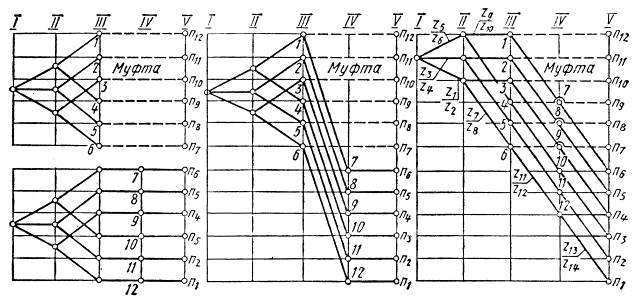
На рис. 3.9 показано графическое сложение структур для рассматриваемой коробки скоростей. На рис. 3.9, а представлены отдельно сетки для каждой структуры. Первая обеспечивает ряд 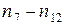, вторая – ряд 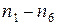. Условимся муфты изображать штриховым лучом (на структурной сетке он может занимать любое положение, на графике частот вращения – только горизонтальное). Тогда все точки, изображающие частоты вращения вала III, соединим горизонтальными штриховыми лучами с точками 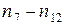вала V. Первые две группы передач (3₁ и 2₃) у обеих структур одинаковы. Принимаем их как общие и придаем первой структуре 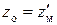. Наносим последнюю на сложенную сетку (рис. 3.9, б). Точки, изображающие частоты вращения вала III, располагаются в верхней части графика. Соединяем их штриховыми линиями с точками 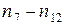. Из них же проводим лучи, изображающие соединительную передачу 1 – 7, 2 – 8, …, 7 – n₆, 8 – n₅ …

а) б) в)

Рис. 3.9. Структурная сетка и график частот вращения коробки скоростей

со сложенной структурой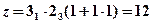

На рис. 3.10 показана другая схема коробки скоростей со сложенной структурой. Вращение от вала I к валу II сообщает группа колес р_a. Далее движение на шпиндель V передается по двум цепям: при левом и среднем положениях блока 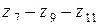– через передач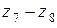и или 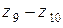(группа р_b); при правом положении блока – группой передач р_с, р_d и р_e. Таким образом, число ступеней скоростей

.

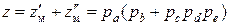Для нашего случая р_a = 3₁; р_b = 2_3; р_с = 1; р_d = 1 и р_e = 2₃. Следовательно, .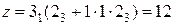

Ha рис. 3.7, в условно показана принципиальная структура, состоящая из трех кинематических цепей: основной z_о и двух дополнительных z_д1 и z_д2.

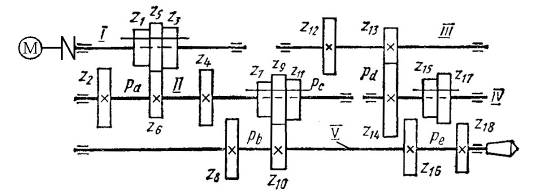
Рис. 3.10. Схема коробки скоростей со сложенной структурой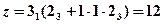

Сложенные структуры обладают рядом достоинств. Они могут обеспечить большое число ступеней скорости при широком диапазоне регулирования. Высокие скорости передаются короткими кинематическими цепями, что уменьшает потери мощности и повышает КПД. Это видно из графиков, показанных на рис. 3,9, б, в: верхняя область частот вращения осуществляется цепью, состоящей только из двух групп. И, наконец, сложенные структуры дают возможность получить любое число ступеней скорости, не только кратное 2 и 3, например, 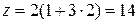; ; 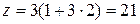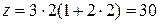и т.д.

3.4.4. Особые множительные структуры

В ряде случаев целесообразно, отклоняясь от классических принципов, упрощать схему привода. Длительная работа станка без изменения частоты вращения шпинделя позволяет использовать в качестве множительной группы звено настройки со сменными колесами. Последние обычно включены в цепь постоянных передач в зависимости от степени редукции или в коробку передач со сравнительно малым количеством ступеней скорости. Например, в коробке, представленной на рис. 3.11, первая группа состоит из сменных колес a – b, а вторая и третья содержат по две пары передач. Следовательно, имеется возможность ступенчатого регулирования частоты вращения шпинделя путем переключения блоков, а установка сменных колес смещает область регулирования вдоль ряда частот вращения [6].

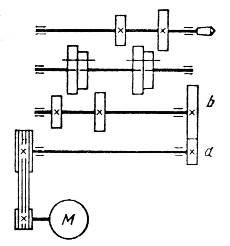
Рис. 3.11. Привод главного движения со сменными колесами

Сменные колеса желательно размещать в первой основной группе, так как число пар колес может быть большим (2-10). Сменные колеса следует подбирать так, чтобы каждая пара могла быть использована дважды, с переменой мест ведущего и ведомого колес. Поэтому нет необходимости иметь пару колес с 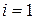. График частот вращения нужно строить по возможности симметричным (рис. 3.12).

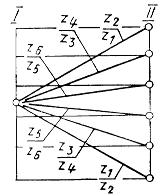
Рис. 3.12. График частот вращения для сменных колес

Если принять для коробки скоростей (см. рис. 3.11) 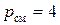, то число ступеней скорости при этой простой схеме .

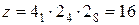Множительные структуры с измененными характеристиками групп передач. Нередко причиной отказа от обычной множительной структуры является высокое значение характеристики последней группы и, в связи с этим, недопустимо малое передаточное отношение одной из передач. Путем искусственного уменьшения характеристик можно с некоторыми отклонениями сохранить желаемую структуру.

Примем для примера 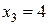и построим график для структуры 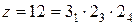(рис. 3.13). Из графика следует, что 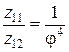. Но одновременно с этим уменьшились диапазон регулирования 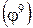и число ступеней скорости ( 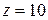), так как две скорости (на графике отмечены двойными кружками) повторяются.

Рассмотрим другой случай, вернувшись к схеме 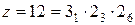. Увеличим характеристики первой и второй групп до значени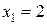й и 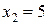. Структура примет вид 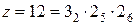. Строим график частот вращения (рис. 3.14, а). Он свидетельствует о сохранении минимального передаточного отношения и одновременно о расширении диапазона регулирования 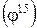путем исключения отдельных скоростей в нижней и верхней частях ряда, где знаменатель принимает ветчину 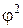. Такой ряд называют ломаным. Если, например, 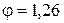, то диапазон регулирования при обычном кинематическом варианте 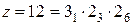и 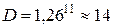, а в данном случае 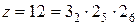и .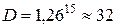

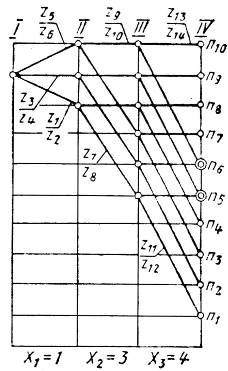
Рис. 3.13. График частот вращения шпинделя с повторяющимися угловыми скоростями

а) б)

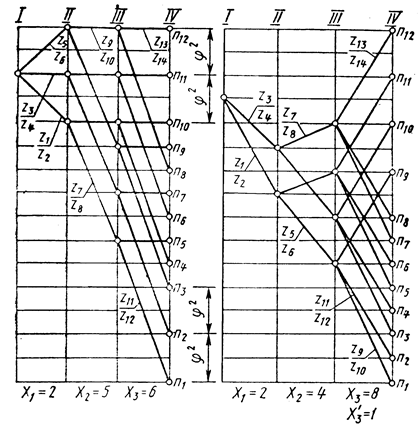
Рис. 3.14. График частот вращения шпинделя коробки скоростей с измененными