ИЗМЕРИТЕЛИ МАЛЫХ СКОРОСТЕЙ

В третьей главе при рассмотрении скоростей полета самолета в пределах манометрического способа измерения было установлено, что наибольшая сложность заключается в измерении малых скоростей. Показано, что доминирующей статической инструментальной погрешностью измерения приборной скорости в диапазоне малых скоростей является погрешность от приведенной силы трения механизма (см. формулу 3.21). В диапазоне околонулевых скоростей погрешность возрастает до бесконечности из-за малого градиента по давлению (таблица 3.7, рис. 3.21).

При рассмотрении полной структурной схемы указателя приборной скорости (рис. 3.5) было сделано замечание, что в динамическом режиме работы прибора следует учитывать все элементы схемы, в том числе пневмопроводы, объемы полостей корпуса, манометрической коробки. Для статического режима справедливо и то, что приборная скорость зависит только от динамического давления, что она не зависит от статического давления и, значит, не обладает методической погрешностью от изменения высоты. С этим утверждением можно мириться до тех пор, пока измеряются медленно меняющиеся давления на входе прибора. Картина резко меняется при рассмотрении динамического процесса измерения скорости.

Эффективнее всего это явление рассмотреть применительно к условиям работы указателя приборной скорости на вертолете.

Принципиальной особенностью вертолета является наличие несущего винта (НВ), создающего воздушные вихри по всей поверхности его фюзеляжа. Интенсивность вихрей зависит от массы вертолета, от его конструкции. Как было показано во второй главе (таблица 2.5), скорость распространения вихря (скорость отбрасывания НВ) может достигать величин от ≈ 50 до 130 км/ч. В режиме висения весь этот поток направлен вертикально к Земле и омывает фюзеляж. Приемники давлений Р_ст и Р_п тоже омываются этим потоком, попадая частично или полностью в их входы. На фоне такой большой помехи невозможно измерить ничтожно малые сигналы по давлению, которые соответствуют околонулевым скоростям (рис. 5.1).

При косом движении вертолета вихрь от НВ уходит от носовой части фюзеляжа и приемники давлений очищаются от него при уже достаточно большой скорости полета (50 – 70 км/ч). За этим пределом измерение скорости может происходить известным манометрическим способом. И наоборот, до скорости очищения приемников от вихря их каналы полностью закрыты помехой от НВ. Процесс измерения невозможен. Указатель скорости фиксирует только помеху от НВ.

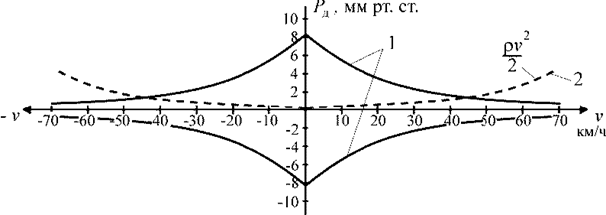
Рис. 5.1. Соотношение погрешности от вихря несущего винта с полезным

сигналом указателя приборной скорости на вертолете: 1 – границы вихря;

2 – полезный сигнал

Учитывая, что манометрический способ измерения скорости давно стал традиционным, надежным, хорошо освоенным в производстве и в эксплуатации, заманчивым является попытка использовать его для измерения малых скоростей полета, хотя бы по направлению движения вертолета по оси О – х. Для этого воспользуемся теорией структурного анализа и теорией абсолютно инвариантных систем автоматического управления.

Принципы абсолютной инвариантности

Смысл достижения абсолютной инвариантности (независимости) заключается в том, что если удалось достичь ее по какой-то координате Х(t) по отношению к помехе F(t), то при отсутствии других помех и нулевом начальном значении, эта переменная тождественно равна нулю на выходе [43].

Со стороны координаты Х(t) никаких воздействий на систему нет, хотя физические аппаратурные связи есть. Данная теория позволяет произвести синтез систем наилучшего качества при весьма ограниченной априорной информации о внешних возмущениях или помехах в системе. Максимально, что может быть известно о помехах, это ограничения их по модулю.

Математически это выглядит так, что если имеется передаточная функция по каналу действия помехи

,

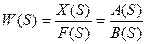то необходимым условием абсолютной инвариантности является: A(S) = 0, B(S) ≠ 0. Тогда: Х(S) = W(S) F(S) = 0·F(S) = 0.

Необходимое условие формулируется так.

Для достижения абсолютной инвариантности по координате Х(t) относительно внешнего возмущения F(t) необходимо, чтобы передаточная функция W(S) между точкой приложения внешнего воздействия F(t) и точкой измерения (съема) сигнала Х(t) была равна нулю при предположении, что и все остальные воздействия равны нулю.

Это общее условие для принципа абсолютной инвариантности. Но не всякая система в реальных условиях может быть абсолютно инвариантной. Необходимо из множества реальных систем отбирать те, к которым применима теория абсолютной инвариантности.

Критерий инвариантности, критерий реализуемости условий инвариантности формируется следующим образом: необходимым (но не достаточным) признаком реализации абсолютно инвариантной системы является наличие в схеме по меньшей мере двух каналов передачи возмущающего воздействия F(t) между точкой его приложения и точкой, относительно которой достигается инвариантность (принцип двухканальности).

Поскольку в абсолютно инвариантной системе W(S) = 0, то это может быть в том случае, если передаточную функцию можно представить в виде разности минимум двух передаточных функций:

.

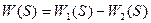Роль структурного анализа в данном случае велика, ибо только правильный выбор структуры позволяет найти абсолютно инвариантные системы, которые могут быть физически реализованы.

Достаточные условия реализуемости связаны с физической выполнимостью требований абсолютной инвариантности при помощи устройств, состоящих только из физически осуществимых звеньев.

С позиций этой теории рассмотрим измеритель приборной скорости летательного аппарата (самолета, вертолета) в режиме полета на малых скоростях.

Под помехой F(t) будем иметь в виду помехи по каналам давлений Р_п и Р_ст, а под выходной координатой – измеряемую скорость. В дальнейшем станет очевидным, что структурная схема этого измерителя есть ничто иное, как естественно двухканальная система автоматического управления.

5.1. Инвариантный измеритель скорости

В настоящее время информацию о скорости самолета получают с помощью аэродинамических измерителей, которые нуждаются в улучшении метрологических характеристик. Как информационный параметр скорость полета (число М) характеризует длиннопериодическое движение с низкими рабочими частотами. Высокочастотные помехи, например шумы решающих и выходных устройств измерителя скорости, нейтрализуются с помощью фильтров. Однако существует динамическая погрешность, пренебрегать которой нельзя и оценка которой возможна при исследовании системы "среда полета – самолет – измеритель скорости". Среда в данном случае характеризуется физическими свойствами атмосферы: изменением статического давления Р_ст в зависимости от высоты полета над уровнем моря, горизонтальными и вертикальными составляющими порывов ветра. Тип самолета определяет максимальное ускорение по направлению полета, скороподъемность, скорость изменения угла атаки. Параметры измерителя скорости отражают степень рациональности его конструкции. Особенностью рассматриваемых измерителей является наличие пневматических емкостей и сравнительно длинных воздухопроводов, в связи с чем постоянные времени каналов полного Р_п и статического Р_ст давлений достаточно велики [44].

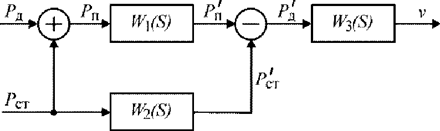
Рис. 5.2. Структурная схема измерителя воздушной приборной скорости самолета

Рассмотрим простейший измеритель воздушной приборной скорости (рис. 5.2) в виде двухканальной системы автоматического регулирования, где W₁(S), W₂(S), W₃(S) – передаточные функции каналов полного, статического давлении, решающего и выходного устройств измерителя. Обратим внимание на то, как формируется в измерителе информация о скоростном напоре Р_д . Видно, что статическое давление Р_ст проходит через оба звена W₂(S) и W₁(S). Скорость v определяется искаженной величиной скоростного напора 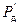, так как он зависит от искаженных величин полного 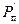и статического 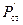давлений. В соответствии со структурной схемой напишем систему уравнений измерителя скорости в операторной форме.

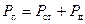, (5.1)

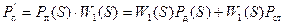, (5.2)

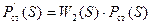, (5.3)

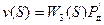, (5.4)

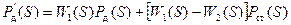. (5.5)

Решая систему уравнений (5.1 – 5.5) относительно скорости v(s), получим полное уравнение измерителя

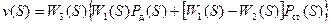. (5.6)

Из уравнения видно, что в отличие от стационарного режима в динамическом режиме скорость v зависит от двух величин: Р_д и Р_ст. Передаточные функции каналов измерителя представим в виде

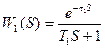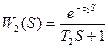; , (5.7)

где τ₁ , τ₂ , Т₁ , Т₂ – время чистого запаздывания и постоянные времени каналов полного и статического давлений. С учетом значений передаточных функции из уравнения (5.6) получим выражение динамической погрешности при скачкообразных возмущениях по Р_д и Р_ст при τ₁ = τ₂ = 0.

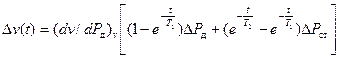, (5.8)

где dv/dP_д – производная зависимости воздушной приборной скорости от скоростного напора при определенном значении скорости полета v; ΔР_д и ΔР_ст – уровни возмущений по каналам Р_д и Р_ст.

Из-за малости величин τ₁ и τ₂ и для упрощения дальнейших исследований их влиянием на погрешность пренебрегаем. Первая составляющая в квадратных скобках выражения (5.8) определяет погрешность по каналу Р_п . Учитывая, что приращение скорости самолета в длиннопериодическом движении происходит медленно и постоянная времени Т₁ по сравнению с Т₂, как правило, мала, то в качестве доминирующей можно рассматривать погрешность, связанную с изменением статического давления или другими возмущениями атмосферы. Эта погрешность определяется вторым слагаемым выражения (5.8)

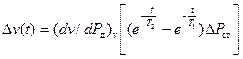, (5.9)

а ее максимальное значение можно представить как

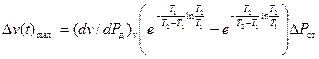. (5.10)

Если возмущение по каналу Р_ст изменяется по пропорциональному закону ΔР_ст (t) = Kt , то исследуемая погрешность будет иметь вид

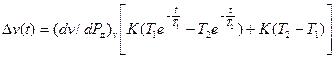, (5.11)

где К – уровень возмущения по каналу Рст.

В данном случае исследуется динамическая погрешность скорости полета самолета с учетом только пневматических параметров каналов Рсти Рп, что совпадает с вариантом, когда собственные динамические характеристики измерителя близки к идеальным. Это дает возможность подчеркнуть физическую сущность исследуемой динамической погрешности, возникающей из-за естественной связи каналов Рп и Рст измерителя. Целесообразность этого подтверждается и тем, что в полете меняются только параметры пневматических каналов.

На рис. 5.3 показана зависимость постоянных времени каналов Рст и Рп, от высоты полета при различных скоростях, где 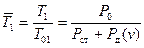– кратность изменения постоянной времени в канале Рп; Т01 – начальное значение Т1 в нормальных условиях; Р0– начальное атмосферное давление; Рд(v) – давление скоростного напора в зависимости от скорости полета; 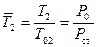– кратность изменения постоянной времени в канале Рст; Т02 – начальное значение T2 в нормальных условиях.

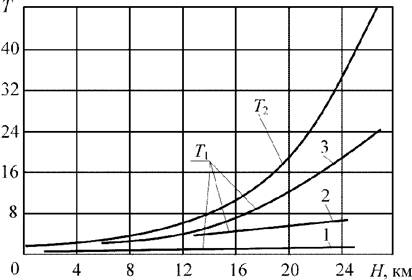
Рис. 5.3. Зависимость постоянных времени Т1 и Т2 от режима полета самолета: 1 – v = 1350 км/ч; 2 – v = 500 км/ч; 3 – v = 200 км/ч

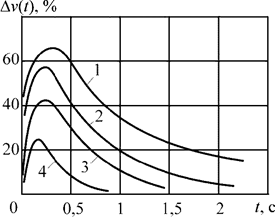
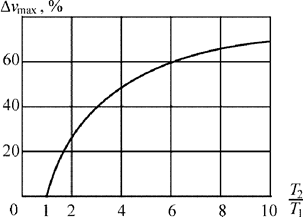
Из рис. 5.3 следует, что Т1 меняется значительно меньше, чем Т2 . Такое расхождение в изменении постоянных времени каналов усиливает связь между ними и увеличивает динамическую погрешность, что следует из уравнений (5.9) – (5.11). Погрешность измерителя скорости возрастает при увеличении отношения Т2/Т1 и при 10-кратном превышении значения T2может достигать 70% (рис. 5.4 – 5.5).

Рис. 5.4. Погрешность измерителя скорости в зависимости от соотношения постоянных времени Т1 и Т2 : 1 – Т2/Т1 = 10; 2 – Т2/Т1 = 6; 3 – Т2/Т1 = 4; 4 – Т2/Т1 = 2	Рис. 5.5. Зависимость максимальной динамической погрешности измерителя скорости от отношения Т1/Т2

Необходимо подчеркнуть, что установленная связь между каналами приводит к необходимости исследования динамической погрешности измерителя скорости также в короткопериодическом движении самолета. Изменение высоты полета и угла атаки, порывы ветра – все эти факторы вызывают появление дополнительной методической погрешности измерителя скорости, которая на некоторых режимах полета может достигать недопустимо большой величины. Например, погрешность от потока несущего винта вертолета может составить 70 км/ч, что приводит на малых скоростях полета к полной неработоспособности измерителя скорости. На пассажирских и транспортных самолетах проявление погрешности наиболее вероятно на режимах взлета и посадки, маршруте при турбулентной атмосфере, при порывах ветра. Эту динамическую погрешность можно устранить или свести к минимуму, если выполнить необходимое для двухканальной системы автоматического регулирования условие инвариантности (равенства передаточных функции каналов):

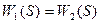. (5.12)

В этом случае погрешности, определяемые уравнениями (5.9) – (5.11) полностью отсутствуют, т.е. измеритель становится инвариантным к аэродинамическим возмущениям в процессе полета.

Согласно теории инвариантности систем условие (5.12) является необходимым, но не достаточным. Нужно показать физическую реализуемость предложенного условия инвариантности. В линейной динамической модели измерителя с передаточными функциями каналов, соответствующими формулам (5.7) условие абсолютной инвариантности к аэродинамическим возмущениям сводится к двум равенствам:

τ₁ = τ₂ , (5.13)

Т₁ = Т₂ . (5.14)

Время чистого запаздывания τ в .каналах зависит от длины воздухопроводов и скорости звука. Из этого следует, что условие (5.13) выполняется простым уравниванием длин пневматических каналов давлений Р_ст и Р_п .

Постоянные времени трактов равны [45]

;

,

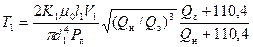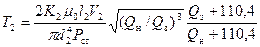где μ₀ — коэффициент динамической вязкости воздуха в нормальных условиях; l₁, l₂ – длина воздухопроводов полного и статического давлений; V₁, V₂ – внутренние объемы пневматических камер каналов полного и статического давлений; d₁, d₂ – внутренние диаметры воздухопроводов полного и статического давлений; Q_н, Q_з – абсолютная температура у земли и на высоте полета самолета.

Учитывая, что каналы Р_п и Р_ст находятся в одних температурных условиях, зависимость (5.14) можно записать в виде Т₂/Т₁ = 1 или

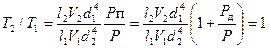. (5.15)

Из выражения (5.15) видно, что выполнение условия инвариантности можно обеспечить, изменяя либо диаметры воздухопроводов, либо внутренние объемы пневматических камер измерителя. В случае изменения диаметра воздухопровода статического давления необходимо соблюдать зависимость

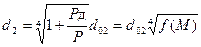, (5.16)

где d₀₂ – начальное значение диаметра d₂ (рис. 5.6).

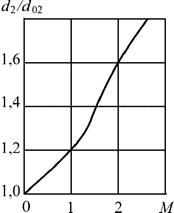
Рис. 5.6. Изменение диаметра трубопровода канала статического давления в зависимости от числа М

Если условие инвариантности поддерживается за счет изменения внутреннего объема пневматической камеры полного давления, закон регулирования объема имеет вид

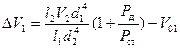, (5.17)

где ΔV₁ и V₀₁ – изменение и начальное значение объема V₁.

Регулирование объема в канале полного давления по закону (5.7) является наиболее удобным способом обеспечения инвариантности.

Измеритель приборной воздушной скорости (рис. 5.7) защищен от аэродинамических возмущений. В стационарном режиме полета давление Р_п, поступающее на вход приемника воздушного давления 1 (ПВД), подается по трубопроводу в переменную пневматическую емкость 2, в объем чувствительного элемента измерителя скорости 3 и преобразователь 4 отношения давлений Р_д и Р_ст . Статическое давление Р_ст по трубопроводу поступает в корпус измерителя скорости 3. Чувствительный элемент воспринимает давление Р_д как разность давлений Р_п и Р_ст . В нестационарном режиме давление возмущения или изменение Р_ст в ПВД заполняет объем корпуса измерителя скорости и поступает в объем чувствительного элемента, переменную пневматическую емкость 2 и преобразователь 4. Сигнал с преобразователя проходит через усилитель 5, включает двигатель 6 и через редуктор 7 воздействует на емкость 2 в соответствии с законом (5.17). Это означает, что в процессе полета автоматически выполняется условие инвариантности (5.12).

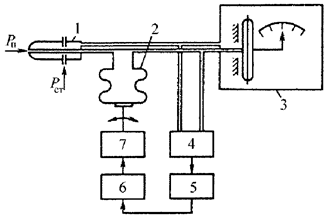
Рис. 5.7. Инвариантный измеритель воздушной приборной скорости самолета

На малых высотах полета ЛА расхождение постоянных времени в каналах Р_ст и Р_п сравнительно невелико (см. рис. 5.3). Поэтому, например, для вертолетного измерителя скорости закон (5.17) можно выполнить только для одного значения отношения Р_п/Р_ст [а.с. 908150 (СССР)]. Это значительно упрощает конструкцию измерителя скорости, но не позволяет достичь абсолютной инвариантности на всех режимах полета. Но даже при использовании упрощенного варианта измерителя скорости на вертолете помехи от аэродинамических возмущений снижаются на целый порядок. Для высокоманевренных самолетов такое упрощение недопустимо.

С учетом полученных алгоритмов, в цифровых измерителях можно компенсировать дополнительную погрешность (а также и динамическую погрешность по каналу Р_п) путем введения их в алгоритмы формирования сигналов. При этом необходимо иметь в виду, что механические индикаторы скоростных параметров останутся нескомпенсированными.

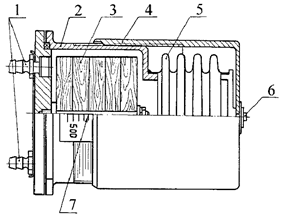
Рис. 5.8. Регулируемая пневматическая емкость: 1 – штуцеры; 2 – герметичный корпус; 3 – вкладыши съемные; 4 – кожух; 5 – сильфон; 6 – винт; 7 – шкала

Для достижения условия инвариантности измерителя в ограниченном диапазоне измерения высоты и скоростей можно воспользоваться устройством с регулируемой пневматической емкостью, величина которой регулируется вручную в процессе полета (рис. 5.8). В качестве регулируемой емкости применен сильфон 5 и съемные вкладыши 3, которые заполняют избыточный объем для конкретной пневмосистемы. С помощью штуцеров 1 устройство подсоединяется к пневмосистеме согласно рис. 5.7. Вращая кожух 4 относительно корпуса 2, сводят колебания стрелки указателя 3 (рис. 5.7) к минимуму. По шкале 7 фиксируют величину объема емкости, необходимую для данного режима полета.