Характеристиками передач
С эксплуатационной точки зрения желательно иметь более тонкое регулирование на малых скоростях и более грубое – на больших. На рис. 3.14, б показан вариант такого расчета. Суть его заключается в том, что в последней группе передач имеются две характеристики: 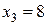 для колес
для колес 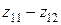 и
и 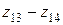 и
и 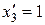 для колес
для колес 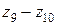 . Такая комбинация дает по
. Такая комбинация дает по 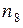 включительно геометрический ряд со знаменателем
включительно геометрический ряд со знаменателем 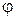 , а выше – со знаменателем
, а выше – со знаменателем 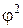 .
.
Коробки скоростей со связанными колесами применяют для уменьшения количества зубчатых колес и осевых размеров коробок скоростей. Сущность данного метода заключается в следующем. Пусть коробка скоростей, изображенная на рис. 3.15, а, имеет две группы передач: 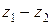 ,
, 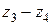 ,
, 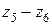 и
и 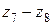 ,
, 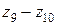 ,
, 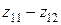 . Если подобрать числа зубьев колес
. Если подобрать числа зубьев колес 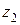 и
и 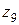 так, чтобы они были одинаковыми
так, чтобы они были одинаковыми 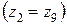 , то представляется возможным оба колеса объединить в одно
, то представляется возможным оба колеса объединить в одно 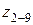 (рис. 3.15, б). Оно одновременно принадлежит и первой, и второй группам, работает в качестве и ведомого, и ведущего звеньев. Подобные колеса называют связанными. По этой схеме строят коробки скоростей типа АКС [20].
(рис. 3.15, б). Оно одновременно принадлежит и первой, и второй группам, работает в качестве и ведомого, и ведущего звеньев. Подобные колеса называют связанными. По этой схеме строят коробки скоростей типа АКС [20].
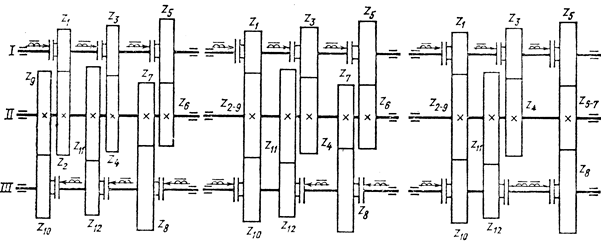
а) б) в)
Рис. 3.15. Схемы коробок скоростей со связанными колесами
Пусть 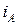 и
и 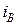 представляют собой передаточные отношения передач, содержащих связанное колесо. Обозначим через
представляют собой передаточные отношения передач, содержащих связанное колесо. Обозначим через 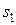 и
и 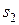 наибольшее количество отрезков
наибольшее количество отрезков 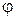 на графике частот вращения, пересекаемое лучами первой и второй групп передач (рис. 3.16). Для получения минимальных габаритов должно быть: при
на графике частот вращения, пересекаемое лучами первой и второй групп передач (рис. 3.16). Для получения минимальных габаритов должно быть: при 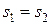
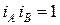 ; при
; при 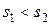
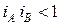 ; при
; при 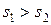
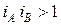 . Если связанным колесом является минимальное, то
. Если связанным колесом является минимальное, то
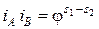 . (3.1)
. (3.1)
Расчеты показали, что при 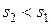 можно уменьшить величину
можно уменьшить величину 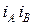 до значения
до значения
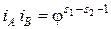 (3.2)
(3.2)
при условии меньшего передаточного отношения 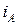 .
.
а) б)
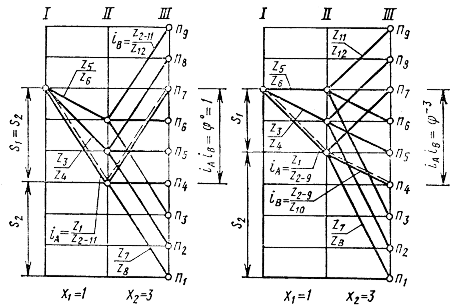
Рис. 3.16. График частот вращения механизмов с одним связанным колесом
Таким образом, выбор варианта связывания заключается в следующем. Если передачи, содержащие связанное колесо, в первой и второй группах симметричны, т.е. 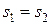 (рис. 3.16, а), то для расчета принимается условие (3.1). Если передача замедленная, то при
(рис. 3.16, а), то для расчета принимается условие (3.1). Если передача замедленная, то при 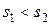 (рис. 3.17, б) из формул (3.1) и (3.2) выбирается та, в которой
(рис. 3.17, б) из формул (3.1) и (3.2) выбирается та, в которой 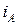 имеет меньшее значение. При
имеет меньшее значение. При 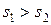 принимается условие (3.1). Покажем это на примерах.
принимается условие (3.1). Покажем это на примерах.
а) б)
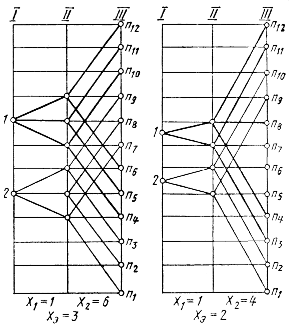
Рис. 3.17. Структурные сетки коробок скоростей с двухскоростным электроприводом
для 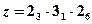 (а) и
(а) и 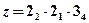 (б)
(б)
На рис. 3.15, в показана схема с двумя связанными колесами, полученная путем объединения колес 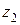 с
с 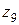 и
и 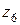 с
с 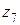 (см. рис. 3.15, б). При этом значительно сокращаются осевые размеры передачи. Но такие механизмы при обычных расчетах обеспечивают геометрический ряд частот вращения при числе зубьев колес, выходящем за принятые пределы.
(см. рис. 3.15, б). При этом значительно сокращаются осевые размеры передачи. Но такие механизмы при обычных расчетах обеспечивают геометрический ряд частот вращения при числе зубьев колес, выходящем за принятые пределы.
В коробках скоростей с приводом от многоскоростных электродвигателей переменного тока в основном применяют двухскоростные со знаменателем ряда 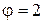 . При данном способе регулирования приемный вал коробки скоростей получает две угловые скорости, и число механических ступеней в связи с этим сокращается вдвое:
. При данном способе регулирования приемный вал коробки скоростей получает две угловые скорости, и число механических ступеней в связи с этим сокращается вдвое: 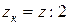 . Помимо упрощения механической части привода, появляется возможность переключения скорости на ходу [6].
. Помимо упрощения механической части привода, появляется возможность переключения скорости на ходу [6].
Двухскоростной электродвигатель можно условно рассматривать как «электрическую группу», состоящую из двух передач. Характеристика 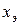 группы может быть найдена исходя из следующих рассуждений. Поскольку скорость вращения шпинделя при переключении электродвигателя с меньшей частотой вращения на большую увеличивается вдвое (
группы может быть найдена исходя из следующих рассуждений. Поскольку скорость вращения шпинделя при переключении электродвигателя с меньшей частотой вращения на большую увеличивается вдвое ( 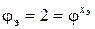 ), то характеристика
), то характеристика 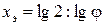 . Для стандартных значений
. Для стандартных значений 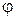 характеристика
характеристика 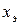 принимается следующей:
принимается следующей:
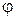 .................................................... 1,12 1,26 1,41 2
.................................................... 1,12 1,26 1,41 2
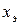 .................................................... 6 3 2 1
.................................................... 6 3 2 1
Для получения нормальной структуры привода без перекрытия частот вращения необходимо выбирать такую структуру коробки скоростей, при которой 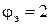 . Поэтому от выбранного значения знаменателя ряда
. Поэтому от выбранного значения знаменателя ряда 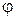 будет зависеть структурная сетка. При расчете это не всегда удается выполнить и может иметь место совпадение скоростей.
будет зависеть структурная сетка. При расчете это не всегда удается выполнить и может иметь место совпадение скоростей.
Пример 1. Дано 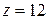 ;
; 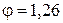 . В качестве электропривода применен двухскоростной электродвигатель трехфазного переменного тока
. В качестве электропривода применен двухскоростной электродвигатель трехфазного переменного тока 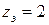 . Требуется построить структурную сетку.
. Требуется построить структурную сетку.
1. Для 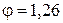 характеристика
характеристика 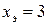 ; следовательно, в структурной формуле ее изображает множитель 23.
; следовательно, в структурной формуле ее изображает множитель 23.
2. Известную нам структурную формулу 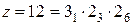 можно для рассматриваемого случая переписать как
можно для рассматриваемого случая переписать как 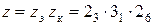 . Отсюда следует, что коробка скоростей должна иметь структуру
. Отсюда следует, что коробка скоростей должна иметь структуру 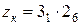 . В табл. 3.4 представлено распределение частот вращения при
. В табл. 3.4 представлено распределение частот вращения при 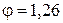 и
и 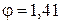 .
.
3. Строим структурную сетку (рис. 3.17, а). Первая группа – «электрическая» с 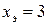 . Наносим на линии I точки 1 и 2 на расстоянии трех интервалов. От каждой точки строим обычным способом сетки для структуры
. Наносим на линии I точки 1 и 2 на расстоянии трех интервалов. От каждой точки строим обычным способом сетки для структуры 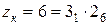 (на рисунке они выделены линиями разной толщины). Частоты вращения n1, n2, n3, n7, n8 и n9 получаются при минимальной частоте вращения электродвигателя nmin, а n4, n5, n6, n10, n11 и n12 – при максимальной частоте вращения
(на рисунке они выделены линиями разной толщины). Частоты вращения n1, n2, n3, n7, n8 и n9 получаются при минимальной частоте вращения электродвигателя nmin, а n4, n5, n6, n10, n11 и n12 – при максимальной частоте вращения 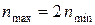 .
.
Таблица 3.4
Частоты вращения вала электродвигателя при 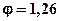 и
и 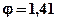
| № ступени коробки скоростей | 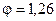
| 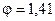
| ||
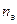
| 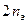
| 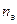
| 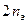
| |
| n1 | n4 | n1 | n3 | |
| n2 | n5 | n2 | n4 | |
| n3 | n6 | n5 | n7 | |
| n7 | n10 | n6 | n8 | |
| n8 | n11 | n9 | n11 | |
| n9 | n12 | n10 | n12 |
Пример 2. Дано 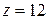 и
и 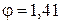 . Построить структурную схему.
. Построить структурную схему.
1. Поскольку 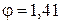 , а характеристика
, а характеристика 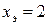 , то в структурной формуле ее изображает множитель 22, а это может быть в варианте
, то в структурной формуле ее изображает множитель 22, а это может быть в варианте 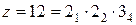 .
.
2. Строим структурную сетку (см. рис. 3.17, б) на основании табл. 3.4 для 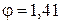 .
.
Выбор наилучшего варианта коробки скоростей довольно сложен [6]. Здесь большое значение имеют группы и типы станков, их техническая характеристика, степень универсальности, точность и другие конкретные параметры. Поэтому при проектировании коробок скоростей нередко возникает ряд вариантов, из которых выбирают наивыгоднейший.
Из всех вариантов кинематической структуры привода, дающих одно и то же число скоростей, оптимальным является тот, который имеет наибольшую простоту, минимальное число групп передач, наименьшее количество зубчатых колес, валов, муфт и других деталей. Масса привода и его размеры должны быть по возможности наименьшими. Из всех кинематических вариантов наиболее выгодным является такой, при котором характеристика групп увеличивается от первого вала коробки скоростей к шпинделю. В большинстве случаев лучшими вариантами являются «веерообразные» структуры, так как в области высоких частот вращения работает большое количество деталей привода. Главная редукция осуществляется на последней ступени, поэтому валы, зубчатые колеса и другие детали привода имеют меньшие размеры, так как при данной мощности передают меньшие крутящие моменты.
На высоких ступенях скорости, особенно у универсальных станков с широким диапазоном регулирования, снижается КПД. Поэтому при выборе кинематического варианта следует стремиться к сложенной структуре, обеспечивающей получение высоких частот вращения шпинделя по более короткой кинематической цепи.
Средством уменьшения радиальных размеров служит условие 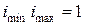 , которое приводит к симметричному расположению линий, изображающих передачи на графиках частот вращения. Другим средством является совмещение осей валов смежных групп передач. Для уменьшения осевых размеров располагают одиночные передачи среди групповых.
, которое приводит к симметричному расположению линий, изображающих передачи на графиках частот вращения. Другим средством является совмещение осей валов смежных групп передач. Для уменьшения осевых размеров располагают одиночные передачи среди групповых.
Использование связанных колес упрощает схему, однако в ряде случаев может увеличить размеры привода.
Дата добавления: 2021-02-19; просмотров: 530;











