Уравнение движения поезда
Методы решения. Аналитическое интегрирование уравнения.
Графическое интегрирование уравнения.
Мы рассмотрели физическую модель поезда и выбрали силы, влияющие на ее состояние. После изучения этих сил можно уточнить в деталях физическую модель поезда и приступим к исследованию ее поведения.
Итак, условно принято, что поезд представляет собой неизменяемую систему, имеющую одну степень свободы: имеет только управляемое поступательное движение; на поезд действуют только три внешние силы Fк, Wк, Вт, направление которых всегда совпадает с управляемым движением или противоположно ему; движение под действием различных сил равна сумме движений под действием каждой из них; равнодействующая сил приложения к центру инерции в середине поезда; поведение поезда вполне определяется описанием движения его центра инерции; управляемые силы Fк, Вт зависят только от скорости и не зависят от времени, т.к. в тяговых расчетах пользуются статическими характеристиками; силы Wк зависят от скорости и координат поезда на линии, т.к. дополнительные сопротивления определяются профилем пути4 скорость и управляемые силы имеют ограничения в получении энергии, а также по условиям безопасности движения поездов, устойчивости движения локомотивов (ограничения силы Fк и тормозной силы Вт по сцеплению).
Физические модели должны соответствовать системам уравнений, описывающих ее поведение. Такую систему уравнения называют математической моделью. Из курса механики известно, что состояние механической системы полностью определяется заданием координат и скорости системы в данный момент времени.
Для физической модели поезда, имеющей одну степень свободы, достаточно одного дифференциального уравнения движения. Для его составления используется теорема об изменении кинетической энергии механической системы – изменение кинетической энергии системы при некотором ее перемещении равна сумме работ внешних и внутренних сил на этом перемещении. Для данной модели необходимо учитывать работу только внешних сил Fк, Wк, Вт, т.к. у неизменяемых систем работа внутренних сил равна нулю.
Рассмотрим режим тяги, равнодействующая сила в котором Rт составит
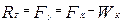 (8.1)
(8.1)
Элементарная работа переменных сил составит
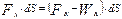 , кГс*м (8.2)
, кГс*м (8.2)
тогда согласно теореме
dT=(FK-WK)*dS , кГс*м (8.3)
Кинетическая энергия поезда в фиксированный момент времени
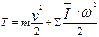 , кГс*м (8.4)
, кГс*м (8.4)
где 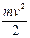 - кинетическая энергия всей массы поезда, движущейся со скоростью в центре инерционных сил, кГс*м;
- кинетическая энергия всей массы поезда, движущейся со скоростью в центре инерционных сил, кГс*м;
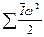 - кинетическая энергия вращающихся тел, колесных пар, якорей ТЭД и зубчатой передачи и т.п., кГс*м;
- кинетическая энергия вращающихся тел, колесных пар, якорей ТЭД и зубчатой передачи и т.п., кГс*м;
m – масса груза поезда, кГс*с2/м;
w – мгновенная угловая скорость, с-1 ;
Ī – полярный момент инерции вращающихся тел.
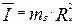 , кГс*с4/м (8.5)
, кГс*с4/м (8.5)
mв и R2и – масса и радиус инерции, кГс*с2/м
Произведем замену ω = v/Rn и Ī получим
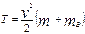 кГс*м (8.6)
кГс*м (8.6)
Выразив mВ как долю m и обозначив
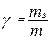 , (8.7)
, (8.7)
тогда 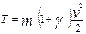 , кГс*м (8.8)
, кГс*м (8.8)
Подставив это выражение в формулу (5.3) получим
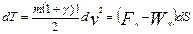 , кГс*м (8.9)
, кГс*м (8.9)
но dS=v*dt, dv2=2v*dv , тогда
m(1+γ)v*dv=(Fк-Wк)v*dt кГс*м (8.10)
но масса поезда m=1000(Q+P)/g, а величина g=9,81 м/с2, т.е. g=127000 км/ч2, тогда
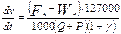 (8.11)
(8.11)
обозначив ζ=127/(1+γ) и (8.12)
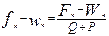 (8.13)
(8.13)
Окончательно получим дифференциальное уравнение движения поезда в режиме тяги
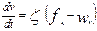 (8.14)
(8.14)
Уравнение выражает зависимость, существующую в каждый момент движения поезда, между равнодействующей силой, массой и ускорением с учетом инерции вращающихся масс.
Для выяснения физической сущности величины ζ прировняем fк – wк = 1 кГс/т, тогда 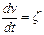 . Значит, ζ представляет ускорение поезда с учетом инерции вращающихся масс. Тогда на каждую точку поезда действует ускоряющая сила в 1 кГс. Величина ζ в зависимости от типа тормозного средства и степени загруженности вагона принимает значение ζ = 107 – 123 км/ч2. В среднем для всех поездов ПТР установлено ζ = 120 км/ч2.
. Значит, ζ представляет ускорение поезда с учетом инерции вращающихся масс. Тогда на каждую точку поезда действует ускоряющая сила в 1 кГс. Величина ζ в зависимости от типа тормозного средства и степени загруженности вагона принимает значение ζ = 107 – 123 км/ч2. В среднем для всех поездов ПТР установлено ζ = 120 км/ч2.
В этом случае основное уравнение движения поезда имеет вид:
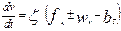 , км/ч2 (8.15)
, км/ч2 (8.15)
Для частных случаев упрощается и принимает вид:
- для движения в режиме тяги с ускорением:
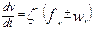 , км/ч2 (8.16)
, км/ч2 (8.16)
- для движения в режиме тяги с равномерной скоростью
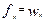 , км/ч2 (8.17)
, км/ч2 (8.17)
- для движения в режиме холостого хода
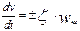 , км/ч2 (8.18)
, км/ч2 (8.18)
- для движения при торможении
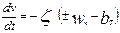 , км/ч2 (8.19)
, км/ч2 (8.19)
При решении практических задач по тяге поездов необходимо знать величину и направление равнодействующих сил, приложенных к поезду. Хотя движение поезда происходит по участку с разнообразным профилем пути, для построения диаграмм равнодействующих сил и анализа по характеру движения поезда достаточно рассчитать действующую силу для случая движения поезда по прямому горизонтальному пути.
Процесс движения поезда, как указывалось выше, характеризуется тремя режимами работы: тяга, холостой ход и режим торможения. Равнодействующие силы в этих режимах составит.
- режим тяги 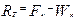 , кГс/т (8.20)
, кГс/т (8.20)
- режим холостого хода 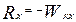 , кГс/т (8.21)
, кГс/т (8.21)
- режим торможения 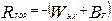 , кГс/т (8.22)
, кГс/т (8.22)
Характер движения поезда определяется величиной и направлением равно-действующей силы. Если равнодействующая сила Ri = 0, то имеет место равномерное движение поезда (или стоянка), если Ri > 0 – движение ускорение, Ri < 0 – движение замедленное.
Для большей наглядности взаимосвязи равнодействующих сил и скорости движения удобно пользоваться, например, в режиме тяги диаграммой равнодействующих сил Fк – Wо = f(v) или удельных равнодействующих сил fк – Wо = φ(v), определяющей величину равнодействующей силы любой скорости движения на элементе пути без дополнительных сопротивлений движению поезда.
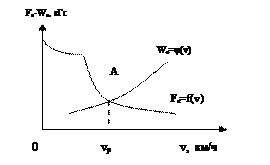 |
Рис. 8.1 – Диаграммы силы тяги Fк и силы основного сопротивления Wо
На рис. 8.1 показана совмещенная диаграмма силы тяги Fк и силы основного сопротивления Wк в функции скорости v. Точка «А» пересечения линии силы тяги с линией силы основного сопротивления определяет скорость vр равномерного движения поезда на прямом и горизонтальном пути 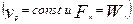
При скоростях, меньших vр , Fк > Wо , т.е. равнодействующая сила положительна и поезд движется с ускорением, а при скоростях, больших vр , Fк < Wо , т.е. равнодействующая сила отрицательна и поезд движется с замедлением. Определив для разных скоростей величину Fк - Wо и разделив результат на массу поезда (Q+Р), можно построить диаграмму удельных равнодействующих сил в режиме тяги
| |
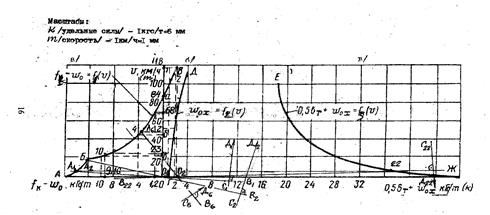
Рис. 8.2 - Диаграмма удельных равнодействующих сил в режимах:
а) тяги, б) холостого хода, в) служебного торможения, она действительна только для определения условий, принятых при ее построении, т.е. для данного состава поезда, данного типа локомотива и вагонов, а также элемента теория без дополнительных сопротивлений Wд = 0, т.е. только с сопротивлением Wк = Wо
Для того чтобы использовать данную диаграмму для элементов профиля с различными удельными сопротивлениями wд необходимо ее перестроение. Для этого необходимо передвинуть начало координат «0» (ось v) на величину удельного сопротивления движению поезда на рассмотренном элементе профиля пути Wgi вправо при знаке (-) и влево при знаке (+).
Уравнение движения поезда имеет один и тот же вид и способы его решения являются общими для различных видов тяги. Основные задачи тяги поездов можно разделить на две группы:
I группа – задачи решенные в предположении движении движения поезда с равномерной скоростью;
– определение веса состава, который может вести данный локомотив, при заданной равномерной скорости по данному элементу профиля пути;
– определение равномерное скорости, которую может развить локомотив данной серии при заданном весе состава по данному элементу профиля пути;
– расчет времени движения поезда на заданном профиле пути методом равномерных скоростей.
В действительности же движение поезда с равномерной скоростью имеет место лишь в редких случаях, в большинстве же случаев движение его неравномерное.
II группа – задачи, решаемые в предположении движения поезда с неравномерной скоростью.
– с разгоном и торможением поезда;
– с использованием кинетической энергии поезда для преодоления крутых подъемов;
– с определением скорости и времени хода поезда по участку с разнообразным профилем пути.
Задачи II-й группы решаются путем интегрирования дифференциального уравнения движения поезда аналитическим или графическим способами. Интегрирование уравнения позволяет найти зависимость между скоростью v, временем t и пройденным расстоянием S.
Разделив переменные в уравнении движения в формуле (8.23) 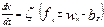 , получим
, получим
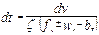 (8.24)
(8.24)
Интегрируя обе части уравнения в пределах изменения скорости от vn до vn+1 получается
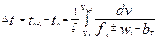 (8.25)
(8.25)
Учитывая, что 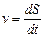 и заменяя в уравнении движения (ф5.15) dt через dS/v, определим путь ∆S, пройденный поездом при изменении скорости от vn до vn+1
и заменяя в уравнении движения (ф5.15) dt через dS/v, определим путь ∆S, пройденный поездом при изменении скорости от vn до vn+1
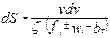 (8.26)
(8.26)
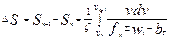 (8.27)
(8.27)
Для интегрирования уравнения (6.6) и (6.7) необходимо иметь характеристики удельных ускоряющих сил для режимов тяги, холостого хода, и торможение с учетом профиля пути. Обычно зависимости сила тяги локомотива от скорости даны графически в виде кривых 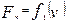 , силы основного сопротивления движению подвижного состава
, силы основного сопротивления движению подвижного состава 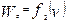 , тормозные силы
, тормозные силы 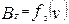 и другие рассчитываются в основном по эмпирическим формулам.
и другие рассчитываются в основном по эмпирическим формулам.
 Для всех графических характеристик можно было бы подобрать аналитические выражения и, пользуясь, ими, непосредственно интегрировать уравнения движения. Но даже при простой замене заданных функций получаются сложные для ручного расчета формулы. В инженерной практике уравнение движения поезда обычно интегрируют, пользуясь методом конечных приращений скорости
Для всех графических характеристик можно было бы подобрать аналитические выражения и, пользуясь, ими, непосредственно интегрировать уравнения движения. Но даже при простой замене заданных функций получаются сложные для ручного расчета формулы. В инженерной практике уравнение движения поезда обычно интегрируют, пользуясь методом конечных приращений скорости 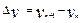 . В пределах этих приращений величина равнодействующей силы принимается постоянной и равной среднему ее значению
. В пределах этих приращений величина равнодействующей силы принимается постоянной и равной среднему ее значению 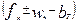 . Следовательно, при способе конечных приращений заданная кривая удельных равнодействующих сил
. Следовательно, при способе конечных приращений заданная кривая удельных равнодействующих сил 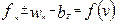 заменяется ступенчатой линией.
заменяется ступенчатой линией.
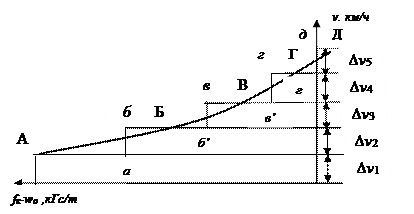
Рис. 8.3 Для режима тяги.
В интервалах скорости 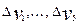 отрезки АБ, БВ, ВГ и ГД кривой
отрезки АБ, БВ, ВГ и ГД кривой 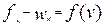 заменяются отрезками аб, бв, вг и гд прямых параллельных оси скорости и соответствующих средним значениям удельных сил, действующих на поезд в этих интервалах. При таких условиях уравнения (6.5) и (6.7) легко интегрируется.
заменяются отрезками аб, бв, вг и гд прямых параллельных оси скорости и соответствующих средним значениям удельных сил, действующих на поезд в этих интервалах. При таких условиях уравнения (6.5) и (6.7) легко интегрируется.
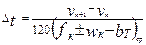 , час (8.28)
, час (8.28)
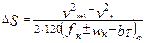 , км (8.29)
, км (8.29)
или 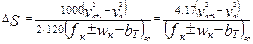 , м (8.30)
, м (8.30)
Итак, при постоянной удельной равнодействующей силы 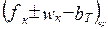 в пределах каждого интервала ∆v движение поезда принимается равномерно-ускоренным или равномерно- замедленным, то есть отрезки кривой
в пределах каждого интервала ∆v движение поезда принимается равномерно-ускоренным или равномерно- замедленным, то есть отрезки кривой 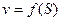 заменяются прямыми отрезками. С уменьшением ∆v точность расчетов возрастает. ПТР предусмотрено интервалы скорости ∆v не более 10 км/ч, для режимов тяги и холостого хода, а для режима торможения ∆v≤5 км/ч в диапазоне скорости 0÷50 км/ч и ∆v≤10 км/ч для v>60 км/ч.
заменяются прямыми отрезками. С уменьшением ∆v точность расчетов возрастает. ПТР предусмотрено интервалы скорости ∆v не более 10 км/ч, для режимов тяги и холостого хода, а для режима торможения ∆v≤5 км/ч в диапазоне скорости 0÷50 км/ч и ∆v≤10 км/ч для v>60 км/ч.
Графические способы отличаются от аналитических тем, что значения скорости V, времени Dt и пути DS не вычисляются, а определяются геометрическими построениями в виде отрезков в определенных масштабах. Все они основаны на приближенном интегрировании уравнения движения поезда. Масштабы скорости, сил, пути и времени при построении кривых обозначают следующим образом: 1 км/ч – m мм, 1 кгс/т – к мм, 1 км – у мм и 1 мин – х мм. Это способы МПС.
При графических способах интегрирования уравнения движения поезда кривую V-f(S) строят по диаграмме удельных равнодействующих сил. Причем здесь так же, как и при аналитическом решении, пользуются методом конечных приращений и в пределах каждого интервала скорости DV по прежнему принимается равнодействующая сила постоянной и равной ее среднему значению ( 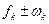 -bт)ср. Предположим, что кривая удельных равнодействующих сил режима тяги
-bт)ср. Предположим, что кривая удельных равнодействующих сил режима тяги 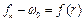 и кривая
и кривая 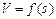 построены (т.е. рис.)
построены (т.е. рис.)
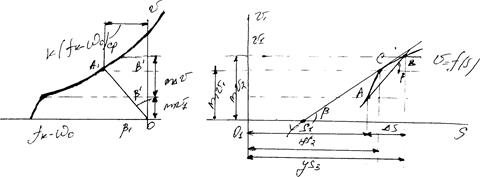
Рис. 8.4 – Диаграмма 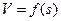 методом МПС.
методом МПС.
Возьмем произвольные две скорости V1 и V2. В этом случае интервал скорости DV= V1 - V2, средняя скорость 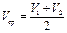 , удельная равнодействующая сила равна
, удельная равнодействующая сила равна 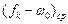 , а отрезок кривой
, а отрезок кривой 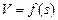 ограничивается точками А и Б.
ограничивается точками А и Б.
Проведем хорду 2-3 точки АБ. Угол между хордой и осью пути S обозначим через b. По сколько функция 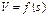 в замкнутом интервале (а,Б) непрерывна и имеет непрерывную производную в этом интервале, то между точками А и Б в кривой существует такая точка С кривой, касается в которой // хорде АБ. tg<b касательной с осью пути S с учетом масштаба построения равен:
в замкнутом интервале (а,Б) непрерывна и имеет непрерывную производную в этом интервале, то между точками А и Б в кривой существует такая точка С кривой, касается в которой // хорде АБ. tg<b касательной с осью пути S с учетом масштаба построения равен:
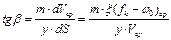 , (8.31)
, (8.31)
а 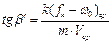 (8.32)
(8.32)
приравняв правые части уравнений (30) и (31)
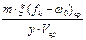 =
= 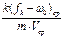 . (8.33)
. (8.33)
И после сокращений будем иметь
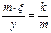 . (8.34)
. (8.34)
Таким образом, из 3-х масштабов (скорости, пути и времени) произвольно можно задаться двумя, а третий вычислить по формуле (32). Обычно при графических построениях задаются масштабами скорости «m» и удельных сил «k», а масштаб пути «у» определяется по формуле:
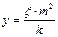 (8.35)
(8.35)
Этим условием обеспечивается графическая связь между кривыми удельных равнодействующих сил и скорости 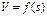 , т.е. теперь по имеющейся диаграмме удельных равнодействующих сил поезда можно построить графически кривую скорости движения данного поезда на заданном участке профиля пути. Кривую
, т.е. теперь по имеющейся диаграмме удельных равнодействующих сил поезда можно построить графически кривую скорости движения данного поезда на заданном участке профиля пути. Кривую 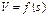 строят следующим образом. На миллиметровой бумаге вычерчивают диаграммы удельных равнодействующих сил для элемента участка профиля пути без дополнительного сопротивления и трех режимов работы: тяги, холодного хорда и служебного торможения с началом координат в точке «О». Наносят координатные оси V и S для построения кривой скорости
строят следующим образом. На миллиметровой бумаге вычерчивают диаграммы удельных равнодействующих сил для элемента участка профиля пути без дополнительного сопротивления и трех режимов работы: тяги, холодного хорда и служебного торможения с началом координат в точке «О». Наносят координатные оси V и S для построения кривой скорости 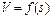 , так чтобы V были //, а абсциссы действующих сил
, так чтобы V были //, а абсциссы действующих сил 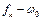 - вт и пути располагались на одной прямой.
- вт и пути располагались на одной прямой.
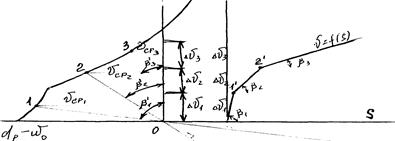
Рис. 8.5 – Диаграмма 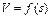
Затем при построении кривой 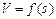 для каждого интервала скорости DV1…. DVn определяется величина средней удельной равнодействующей силы и строятся
для каждого интервала скорости DV1…. DVn определяется величина средней удельной равнодействующей силы и строятся 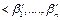 равны углам
равны углам 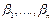 , одна из сторон которой совпадает с осью S, а другая определяет хорду искомой кривой
, одна из сторон которой совпадает с осью S, а другая определяет хорду искомой кривой 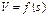 .
.
Для построения хорд достаточно в каждом интервале скорости DVi провести линию перпендикулярно соответствующему лучу О11¢^O1, 1¢2¢^O2 и т.д., таким образом и получаем кривую скорости 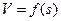 движения поезда на рассматриваемом элементе профиля пути.
движения поезда на рассматриваемом элементе профиля пути.
Построение кривой времени.
Кривая времени 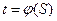 строится по построенной кривой скорости
строится по построенной кривой скорости 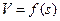 . Предположим, что кривая
. Предположим, что кривая 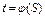 построена (рис. 8.5)
построена (рис. 8.5)
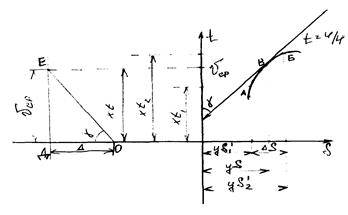
| Построение диаграммы 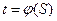 методом МПС.
Возьмем на этой кривой произвольно две точки А и Б и проведем через них хорду АБ. Поскольку функция методом МПС.
Возьмем на этой кривой произвольно две точки А и Б и проведем через них хорду АБ. Поскольку функция 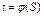 в замкнутом контуре (А, Б) непрерывная и имеет непрерывную производную в этом в замкнутом контуре (А, Б) непрерывная и имеет непрерывную производную в этом
|
интервале, между А и Б существует такая точка В кривой, касается в которой параллельна хорде АБ. 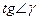 касательной с осью времени с учетом масштаба построения равен
касательной с осью времени с учетом масштаба построения равен
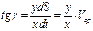 (8.36)
(8.36)
Для получения на графике величины, пропорциональной скорости, построим слева от кривой времени прямоугольный треугольник, у которого длина одного его катета равна в масштабе средней скорости Vcp, а другого – постоянна и равна величине D мм, тогда
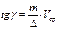 (8.37)
(8.37)
Приравняв правые части уравнений (8.36) и (8.37) получим:
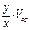 =
= 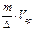 (8.38)
(8.38)
Сокращая и подставляя значения у из уравнения (6.15), масштаб времени х определяется:
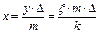 (8.39)
(8.39)
Кривую времени движения поезда 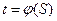 строят следующим образом: на миллиметровой бумаге вычерчивают кривую скорости
строят следующим образом: на миллиметровой бумаге вычерчивают кривую скорости 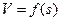 (рис.)
(рис.)
| |
|
|
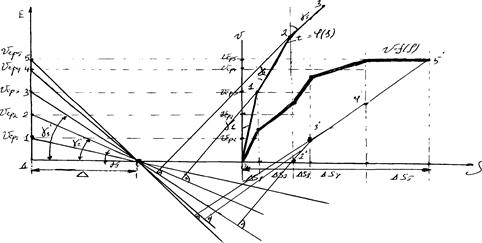
Затем на оси пути S от произвольной точки «О» влево откладывают постоянный катет треугольника. Из точки Д восстанавливается ^ДЕ к оси пути s, на котором находятся средние скорости Vcp1 …Vcpn. Соединяя точки 1, …n с точкой О лучами О1,…., Оn, находим углы 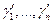 . Чтобы провести хорды кривой
. Чтобы провести хорды кривой 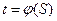 под <
под < 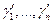 в пределах DS1,… DSn, достаточно провести линии О11¢; 1¢2¢, …., (n-1)¢n¢ ^ к лучам О1, …., Оn.
в пределах DS1,… DSn, достаточно провести линии О11¢; 1¢2¢, …., (n-1)¢n¢ ^ к лучам О1, …., Оn.
В ПТР при построении кривых скорости и времени движения поезда рекомендуются следующие масштабы для графических построений.
| Величины | Для грузовых поездов | Для тормозных расчет. | |||
| Удельные силы 1 кгс/т – к, мм | |||||
| Скорости, 1 км/ч – m, мм | |||||
| Пути, 1 км – у, мм | |||||
| Постоянная - D мм | - | - | |||
| Времени, 1 мин – х, мм | - | - |
Дата добавления: 2016-11-04; просмотров: 10066;











