Обработка результатов многократных измерений одной и той же величины

Некоторые правила обработки результатов измерений

Погрешность однократного измерения

Максимально возможную погрешность однократного измерения можно определить, зная класс точности прибора. У электронных приборов со стрелочным индикатором или у стрелочных приборов класс точности обычно обозначен прямо на шкале. В этом случае максимальная погрешность измерения (абсолютная) определяется как D = К × А × 0.01, где К- класс точности, А - верхняя граница диапазона (шкалы). Иногда правила определения погрешности указаны в паспорте прибора. Если других данных нет, за величину абсолютной погрешности принимают половину цены деления шкалы или единицу младшего разряда (для цифровых индикаторов).

Если, например, получено значение некоторого напряжения 143,12 В, а вычисление погрешности дало 4,38 В, то можно заметить, что уже цифра “3” в разряде единиц вольт определена с малой точностью, поскольку погрешность превышает 4 В. Тем более, десятые и сотые доли вольта в результате вообще физического смысла не имеют. Кроме того, если определить относительную погрешность, с которой определяются сами величины погрешностей, то окажется, что она составляет обычно 20 ¸ 30 %. В связи с этим производят округление полученной величины погрешности до одной значащей цифры (или до двух, если первая - единица), по известному правилу: если первая из отбрасываемых цифр меньше 5, то последняя сохраняемая не изменится, если больше 5 - увеличивается на единицу. В случае, если первая из отбрасываемых цифр равна 5 и является последней, не равной 0, то сохраняемая цифра не меняется, если она четная, и увеличивается на единицу, если она нечетная.

Примеры правильного округления погрешностей:

4,36 » 4; 2,68 » 3; 6,501 » 7; 1,23 » 1,2; 6,500 » 6;

7,5 » 8; 536 » 5 × 10² или 0,5 × 10³

Результат измерения округляют по этому же правилу для того, чтобы его разрядность совпала с разрядностью соответствующей погрешности. Окончательную запись производят, например, в следующем виде:

U = (12,3 ± 0,3) В, или U = 12,3 В ± 0,3 В.

Измеряемые величины и их погрешности необходимо записывать в одних и тех же единицах.

В связи с вышеизложенным представляется полезным прикинуть величину погрешности перед проведением измерений. Иначе может оказаться, что измерения нужно проводить заново. Например, вы прочитали по прибору и записали результаты с точностью до десятых долей какой-то единицы измерений, а вам для получения окончательного результата оказались нужны еще и сотые доли. Получение более точных, чем нужно, данных, в свою очередь, сопряжено с повышенными затратами времени.

Обработка результатов многократных измерений одной и той же величины

Иногда необходимо определить некоторую величину X из результатов ее многократных измерений х₁, х₂ ... х_n. В этом случае обычно величину X принимают случайной с нормальным (гауссовским) законом распределения и, в соответствии с законами теории вероятностей, обработку результатов производят следующим образом:

1. Вычисляют .

2. Вычисляют

3. Если n ³ 30, то полагают, что - s £ х £ + s с вероятностью 68 %, -2s £ х £ +2s с вероятностью 95 %, -3s £ х £ +3s с вероятностью 99,7 %. Если n < 30, то соответствующие вероятности будут несколько меньше, или для получения этих же вероятностей нужно взять несколько большие интервалы. Например, при n = 3 вместо s нужно брать » 2s, при n = 10 ‑ соответственно, » 1,1 s. Поэтому 10 ¸ 15 измерений обычно бывает достаточно.

4. Если для какого-либо i х_i > +3s или x_i < -3s, то результат х_i объявляется грубой ошибкой (промахом), он отбрасывается, и операции пунктов 1 ¸ 4 производят заново, уже без значения х_i. При этом, естественно, n становится меньше на единицу.

5. Учитывают влияние на результат кроме найденной случайной составляющей погрешности, еще и систематической составляющей. За систематическую D_сист принимают погрешность, определяемую по классу точности для каждого измерения (или максимальную из них). Получают “полную” погрешность (абсолютную) по формуле Dх = 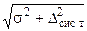. Полученную величину Dх и результат округляют и записывают в соответствии с правилами п. 1.