ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ТРЕНИЯ СКОЛЬЖЕНИЯ

И ТРЕНИЯ КАЧЕНИЯ С ПОМОЩЬЮ НАКЛОННОГО МАЯТНИКА

Цель работы: изучить явления трения скольжения и трения качения; определить коэффициенты трения скольжения и трения качения.

Приборы и принадлежности: наклонный маятник со шкалами для измерения углов; исследуемые пластины-образцы, шарики, бруски.

Краткая теория

Во всех реальных механических процессах имеют место силы трения. Их действие в большинстве случаев связывают с превращением механической энергии во внутреннюю энергию (тепловую).

Различают внешнее трение, возникающее в плоскости касания двух прижатых друг к другу тел при их относительном перемещении, и внутреннее трение, возникающее при перемещении слоев одной и той же среды относительно друг друга (его изучают в разделе ″молекулярная физика″). В данной работе рассматривается внешнее трение.

В зависимости от вида перемещения одного тела по другому различают трение скольжения и трение качения, а по наличию промежуточной прослойки между телами различают трение сухое (твердая прослойка) и трение граничное (жидкая или консистентная прослойка). Каждый из видов внешнего трения характеризуют соответствующим коэффициентом.

Характерной особенностью внешнего трения является наличие трения покоя. Из опыта известно, что когда сила, стремящаяся привести тело в движение, недостаточно велика, тело остается в покое. Это значит, что возникает сила трения, уравновешивающая приложенную извне силу – сила трения покоя. Таким образом, сила трения может существовать между соприкасающимися, но не движущимися телами. С увеличением приложенной силы увеличивается и сила трения покоя. В конце концов тело начинает двигаться. Значит, сила трения покоя может увеличиваться только до некоторого определенного предела. Когда говорят о силе трения покоя, имеют в виду ее максимальное значение, равное силе, приводящей тело в движение.

Трение скольжения

Для определения коэффициента трения в данной работе используется метод наклонного маятника (рис. 13.1). Шарик или брусок, подвешенные в точке О, опираются на наклонную плоскость, угол наклона которой к горизонту b можно изменять. Если отклонить маятник от положения равновесия на угол a₀, то он начнет совершать затухающие колебания. В результате за n колебаний угол отклонения уменьшится до значения 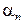. Затухание колебаний происходит главным образом под действием внешнего трения.

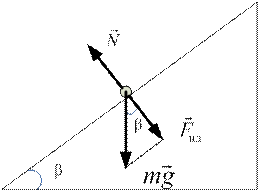
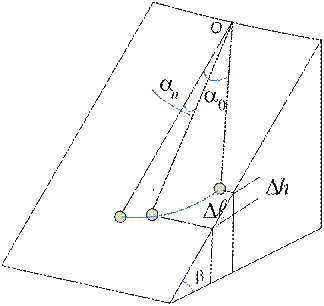
а б

Рис. 13.1

Коэффициент трения скольжения 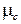равен отношению силы трения 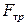к силе реакции опоры N (которая, согласно III закону Ньютона, всегда равна силе нормального давления 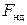, прижимающей тело к опоре)

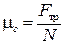. (13.1)

В рассматриваемом случае (рис. 13.1а) сила реакции опоры по модулю равна составляющей силы тяжести 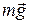, направленной перпендикулярно плоскости

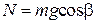, (13.2)

где m – масса маятника, g – ускорение свободного падения.

Сила трения может быть найдена с помощью закона сохранения энергии. Согласно которому работа, совершенная силой трения за n колебаний, равна изменению потенциальной энергии тела за то же число колебаний

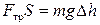, (13.3)

где 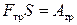– работа силы трения, S – расстояние, пройденное телом за n колебаний, 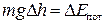– изменение потенциальной энергии тела за то же число колебаний, Dh – изменение высоты тела вследствие затухания колебаний.

С учетом формул (13.2) и (13.3) формула (13.1) принимает вид

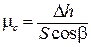. (13.4)

Далее, из рис. 13.1б видно, что

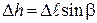, (13.5)

где 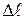– расстояние между начальным и конечным положениями тела, отсчитанное по наклонной плоскости.

Подставив (13.5) в (13.4), получим для коэффициента трения скольжения формулу

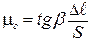. (13.6)

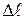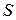Теперь осталось выразить величины и через величины, измеряемые на опыте: число колебаний и углы отклонения маятника от положения равновесия 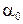и 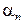. Рис. (13.2) поясняет, как это можно сделать.

На рисунке изображены три положения тела: положение равновесия D, начальное положение F, соответствующее отклонению на угол 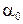, и конечное положение E, соответствующее отклонению на угол 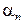. Из рис. 13.2 видно, что 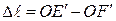. 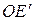и 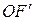можно представить через длину нити маятника L и углы его отклонения от положения равновесия. Действительно, из треугольника EOE¢ следует, что 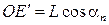, а из треугольника FOF¢ – 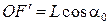. Итак,

.

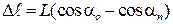Если учесть, что при малых углах 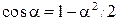то 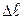можно представить в виде

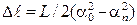. (13.7)

Путь S, пройденный телом, можно найти, руководствуясь следующими соображениями. За одно полное колебание тело проходит расстояние, равное четырем амплитудам 4A. За n колебаний пройденный путь S = 4nA. Но амплитуда вследствие затухания изменяется от начального значения А₀, равного дуге DF, до конечного значения A_n, равного дуге DE, поэтому надо взять ее среднее значение. Из рис. 13.2б видно, что А₀ » a₀L, а A_n » a_nL (здесь углы выражены в радианах), следовательно, среднее значение амплитуды равно L(a₀ + a_n)/2. Итак,

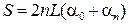. (13.8)

Подставив (13.7) и (13.8) в (13.6), получим формулу для расчета коэффициента трения скольжения в данной работе

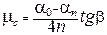. (13.9)

Трение качения

В различных случаях силы трения оказываются как полезными, так и вредными, с которыми приходится бороться. Для уменьшения трения применяются смазки. Однако более радикальным способом уменьшения сил трения является замена трения скольжения трением качения.

Под трением качения понимают трение, возникающее между шарообразным или цилиндрическим телом (например, колесом), катящимся без скольжения (рис. 13.3).

Коэффициентом трения качения 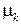называется отношение модуля момента сил сопротивления движению тела (в данной работе момента силы трения 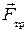) 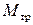к модулю силы нормального давления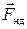

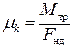. (13.10)

При перекатывании цилиндра по поверхности твердого тела возникает деформация. Из-за чего линия силы, действующей на тело со стороны поверхности 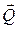, не совпадает с линией силы нормального давления 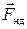, прижимающей тело к поверхности. Составляющая силы 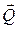, перпендикулярная к поверхности 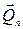, практически равна силе нормального давления 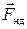, (так как тело в вертикальном направлении не движется), а горизонтальная составляющая представляет собой силу трения 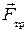. Сила трения приводит к уменьшению скорости перемещения центра масс колеса, т. е. к уменьшению скорости его поступательного движения. Но она создает момент силы, который должен увеличивать скорость вращения тела. Силы же 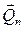и 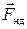создают пару сил, момент которой направлен в обратную сторону и замедляет вращение.

Если цилиндр движется по плоскости равномерно, то моменты сил равны. Момент пары сил равен произведению модуля силы 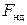на плечо пары, которое равно расстоянию между силами k, а момент силы трения скольжения равен произведению силы трения на ее плечо, которое примерно равно радиусу колеса R. Т. е.,

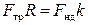, (13.11)

откуда

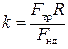. (13.12)

Сравнив (13.12) с (13.10), приходим к выводу, что 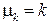(так как 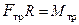). Таким образом, коэффициент трения качения представляет собой плечо силы, следовательно, имеет размерность длины.

Отношение 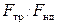, входящее в формулу (13.12), было выведено выше (13.9). Подставив (13.9) в (13.12), получим формулу для расчета коэффициента трения качения

. (13.13)

В данной работе коэффициент трения качения определяется тем же методом наклонного маятника, что и коэффициент трения скольжения. В этом случае маятник представляет собой шарик, подвешенный на нити и катящийся с затуханием по наклонной плоскости. Безусловно, затухание колебаний шарика будет происходить медленнее, чем затухание колебаний бруска, т. е. угол отклонения шарика через n колебаний a_n будет меньше отличаться от a₀.

Радиусы шаров R: стального – 10,2 мм; алюминиевого – 10,3 мм; латунного – 10 мм.