Описание установки и метода измерений

Моменты инерции тел правильной формы относительно главных осей инерции 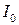можно легко рассчитать по (14.2). Например, для прямоугольного параллелепипеда имеем

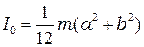, (14.3)

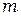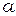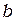где – масса тела, и – высота и ширина грани, перпендикулярной к оси вращения (размер параллелепипеда вдоль оси значения не имеет).

Если известен момент инерции относительно оси, проходящей через центр масс, то момент инерции относительно параллельной ей оси, но не проходящей через центр масс, можно найти по теореме Штейнера (Т. 12).

В остальных случаях (тело имеет неправильную форму или форма тела правильная, но ось вращения не является осью симметрии) момент инерции определяют опытным путем. В настоящей работе – методом крутильных колебаний.

Используемая в данной работе установка (рис. 14.4) состоит из вертикальной стойки с кронштейнами – 2; рамки подвеса – 3, закрепленной на кронштейнах с помощью проволоки; исследуемого тела – 6, имеющего углубления для более надежного закрепления в рамке (всего в комплекте установки три тела с различным типом симметрии). Для наиболее жесткого закрепления тела на рамке имеется передвижная планка 8. После того, как с помощью углублений тело устанавливают в рамке, его положение фиксируют планкой 8 с помощью винтов 9.

Как известно (вывод дан в работе 1.3), период крутильных колебаний связан с моментом инерции тела соотношением

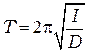, (14.4)

где 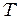– период крутильных колебаний тела относительно данной оси вращения, 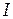– момент инерции относительно этой оси, 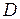– модуль кручения проволоки, на которой подвешено тело (в данном случае рамка подвеса).

Если известен модуль кручения проволоки, то, измерив на опыте период колебаний, легко найти момент инерции тела

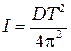. (14.5)

В настоящей работе сначала для одной из главных осей инерции теоретически рассчитывают момент инерции тела, затем, соответствующим образом закрепив тело в рамке подвеса, измеряют период его колебаний и рассчитывают модуль кручения проволоки, который, согласно (14.4), равен

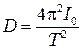. (14.6)

После этого можно определять моменты инерции любых тел относительно каких угодно осей вращения.