Наглядное изображение бинарных отношений
1. Таблица смежности
Наглядное представление о бинарном отношении и его свойствах дает таблица смежности данного бинарного отношения. Пусть A – некоторое конечное множество, и 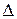 – бинарное отношение на множестве A. Составим таблицу, каждая строка и каждый столбец которой соответствует элементу множества A. Таким образом каждой клетке таблицы соответствует упорядоченная пара элементов множества A. Заметим, что элементы в паре могут совпадать. Отметим те клетки таблицы, которым соответствуют пары элементов, входящие в
– бинарное отношение на множестве A. Составим таблицу, каждая строка и каждый столбец которой соответствует элементу множества A. Таким образом каждой клетке таблицы соответствует упорядоченная пара элементов множества A. Заметим, что элементы в паре могут совпадать. Отметим те клетки таблицы, которым соответствуют пары элементов, входящие в 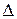 , причем первый элемент пары соответствует строке таблицы, а второй – столбцу. Таблица с отмеченными клетками называется таблицей смежности бинарного отношения
, причем первый элемент пары соответствует строке таблицы, а второй – столбцу. Таблица с отмеченными клетками называется таблицей смежности бинарного отношения 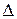 на множестве A. Таблица смежности полностью описывает бинарное отношение на множестве.
на множестве A. Таблица смежности полностью описывает бинарное отношение на множестве.
Пример. Пусть 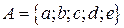 и
и 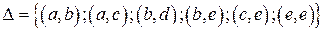 . Тогда таблица смежности данного бинарного отношения будет иметь вид:
. Тогда таблица смежности данного бинарного отношения будет иметь вид:
| a | b | c | d | e | |
| a | ✓ | ✓ | |||
| b | ✓ | ✓ | |||
| c | ✓ | ||||
| d | |||||
| e | ✓ |
По таблице смежности можно установить свойства бинарного отношения. Так, например, в таблице смежности рефлексивного бинарного отношения будут отмечены клетки главной диагонали (идущей из левого верхнего в правый нижний угол таблицы). Если бинарное отношение симметрично, то в его таблице смежности будут отмечены клетки, расположенные симметрично относительно главной диагонали.
2. Графическое изображение бинарного отношения
Пусть A – некоторое конечное множество, и 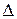 – бинарное отношение на множестве A. Отметим на плоскости точки, каждая из которых соответствует элементу множества A. Если упорядоченная пара элементов множества A входит в
– бинарное отношение на множестве A. Отметим на плоскости точки, каждая из которых соответствует элементу множества A. Если упорядоченная пара элементов множества A входит в 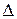 , то проведем стрелку из точки, соответствующей первому элементу пары, в точку, соответствующему второму элементу пары. В результате получим диаграмму, полностью описывающую данное бинарное отношение. Такая диаграмма называется ориентированным графом, точки – вершинами графа, а стрелки – дугами графа.
, то проведем стрелку из точки, соответствующей первому элементу пары, в точку, соответствующему второму элементу пары. В результате получим диаграмму, полностью описывающую данное бинарное отношение. Такая диаграмма называется ориентированным графом, точки – вершинами графа, а стрелки – дугами графа.
Пример. Изобразим ориентированный граф, соответствующий бинарному отношению из предыдущего примера:
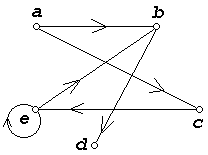
По ориентированному графу можно установить свойства бинарного отношения. Так, например, в ориентированном графе рефлексивного бинарного отношения каждая вершина имеет петлю – дугу выходящую из данной вершины и входящую в нее же. Если бинарное отношение симметрично, то каждой паре вершин графа соответствует две дуги: одна из них идет из одной вершины в другую, а другая – обратно.
Дата добавления: 2021-02-19; просмотров: 847;











