Лексикографический порядок. Порядок по Парето

Рассмотрим два специальных вида отношений порядка, имеющие большое прикладное значение: лексикографический порядок и порядок по Парето.

Лексикографический порядок

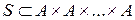Определение 3.1. Пусть A – множество с введенным на нем отношением строгого порядка . Рассмотрим множество S – подмножество n-кратного декартова произведения множества A на себя: . Введем на множестве S отношение порядка p_Lследующим образом:

пусть 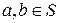, тогда 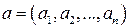и .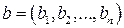

Положим a p_L b .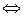

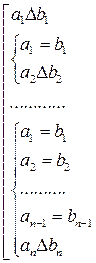Тогда бинарное отношение p_L на множестве S называется лексикографическим порядком.

Если a p_L b, то говорят, что a лексикографически предшествует b, а b лексикографически следует за a.

Замечание. Из определения следует, что лексикографический порядок на множестве S основан на отношении строгого порядка на множестве A.

Лексикографический порядок является строгим, это следует из того, что бинарное отношение – строгий порядок. При этом множество S , очевидно, совершенно упорядочено.

Примеры. 1) Пусть 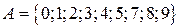– множество цифр. Введем на множестве A отношение строгого порядка естественным образом: одна цифра предшествует другой, если соответствующее ей число меньше числа, соответствующего другой цифре. Положим 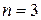. Тогда все числа от 0 до 999 можно представить в виде элементов множества 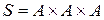, считая, что двузначные числа начинаются с цифры 0, а однозначные с двух нулей. Тогда естественный порядок трехзначных чисел соответствует лексикографическому порядку на множестве S.

2) Пусть A – множество букв алфавита английского языка с добавлением буквы “пробел”, предшествующей букве А. Рассмотрим множество английских слов в некотором англо-русском словаре. Пусть n – длина самого длинного английского слова в словаре. Дополним каждое слово длины меньшей, чем n, пробелами в начале слова, так, чтобы длина слова стала равна n . Пусть S – множество английских слов в словаре с учетом их дополнений пробелами. Тогда все элементы множества S расположены в лексикографическом порядке, основанном на порядке букв в алфавите.

Порядок по Парето

Определение 3.2. Введем на множестве 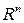бинарное отношение следующим образом: пусть 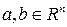, тогда 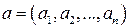и 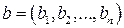. Положим a p_Pb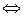 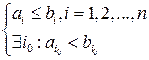. Тогда бинарное отношение p_P на множестве 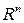называется порядком по Парето. Если ap _P b, то говорят, что a предшествует b по Парето, а b следует за a по Парето.

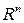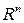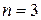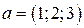Очевидно, что порядок по Парето строгий. При этом множество не является совершенно упорядоченным. Действительно, существуют точки в не сравнимые между собой по Парето. Например, при точки и 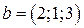не сравнимы по Парето.