Свойства бинарных отношений. Отношение эквивалентности. Отношения порядка
Рассмотрим бинарное отношение 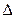 на множестве A.
на множестве A.
1. Рефлексивность. Бинарное отношение называется рефлексивным, если выполняется 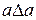 , для всех
, для всех 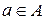 .
.
2. Симметричность. Бинарное отношение называется симметричным, если 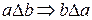 , для всех
, для всех 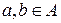 .
.
3. Транзитивность.Бинарное отношение называется транзитивным,
если 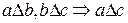 , для всех
, для всех 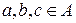 .
.
Примеры. 1) Пусть 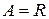 . Рассмотрим бинарное отношение
. Рассмотрим бинарное отношение 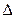 на множестве R, определяемое следующим образом:
на множестве R, определяемое следующим образом: 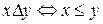 . Тогда
. Тогда 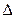 обладает свойством рефлексивности, поскольку
обладает свойством рефлексивности, поскольку 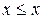 для всех
для всех 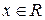 . Бинарное отношение
. Бинарное отношение 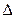 не обладает свойством симметричности, поскольку из неравенства
не обладает свойством симметричности, поскольку из неравенства 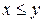 не следует неравенство
не следует неравенство 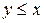 . Бинарное отношение
. Бинарное отношение 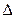 обладает свойством транзитивности, поскольку из неравенств
обладает свойством транзитивности, поскольку из неравенств 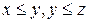 следует
следует 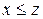 .
.
2) Пусть A – множество всех людей на Земле. Рассмотрим бинарное отношение 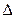 на множестве A, определяемое следующим образом:
на множестве A, определяемое следующим образом: 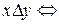 человек x является братом или сестрой человека y (т. е . x и y имеют хотя бы одного общего родителя). Тогда
человек x является братом или сестрой человека y (т. е . x и y имеют хотя бы одного общего родителя). Тогда 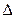 , очевидно, рефлексивно, симметрично, но не транзитивно.
, очевидно, рефлексивно, симметрично, но не транзитивно.
Определение 2.1. Бинарное отношение, обладающее свойствами рефлексивности, симметричности и транзитивности называется отношением эквивалентности.
Примеры. 1) Пусть 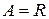 . Рассмотрим бинарное отношение
. Рассмотрим бинарное отношение 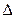 на множестве R, определяемое следующим образом:
на множестве R, определяемое следующим образом: 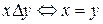 . Тогда
. Тогда 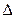 является отношением эквивалентности. Действительно,
является отношением эквивалентности. Действительно, 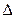 рефлексивно, поскольку
рефлексивно, поскольку 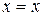 для всех
для всех 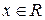 . Бинарное отношение
. Бинарное отношение 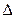 , очевидно, также симметрично и транзитивно.
, очевидно, также симметрично и транзитивно.
2) Пусть A – множество студентов потока. Рассмотрим бинарное отношение  на множестве A, определяемое следующим образом:
на множестве A, определяемое следующим образом: 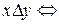 студенты x и y учатся в одной группе. Тогда
студенты x и y учатся в одной группе. Тогда  является отношением эквивалентности. Действительно, рефлексивность
является отношением эквивалентности. Действительно, рефлексивность  означает, что каждый студент учится сам с собой в одной группе. Симметричность
означает, что каждый студент учится сам с собой в одной группе. Симметричность  означает, что если студент x учится в одной группе со студентом y, то и студент y учится в одной группе со студентом x. Транзитивность
означает, что если студент x учится в одной группе со студентом y, то и студент y учится в одной группе со студентом x. Транзитивность  означает, что если студент x учится в одной группе со студентом y, а студент y учится в одной группе со студентом z, то студент x учится в одной группе со студентом z.
означает, что если студент x учится в одной группе со студентом y, а студент y учится в одной группе со студентом z, то студент x учится в одной группе со студентом z.
Отношение эквивалентности часто обозначают знаком 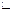 .
.
Определение 2.2. Рассмотрим множество A и 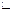 – отношение эквивалентности на множестве A. Пусть
– отношение эквивалентности на множестве A. Пусть 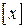 – подмножество множества A, определяемое следующим образом:
– подмножество множества A, определяемое следующим образом: 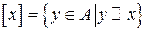 . Тогда множество
. Тогда множество 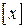 называется классом эквивалентности элемента x, порожденным отношением эквивалентности
называется классом эквивалентности элемента x, порожденным отношением эквивалентности 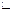 .
.
Свойства классов эквивалентности
1. Классы эквивалентности элементов множества не пусты. Действительно, класс эквивалентности множества x содержит элемент x: 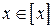 .
.
2. Пусть 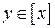 . Тогда
. Тогда 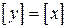 .
.
Доказательство. Пусть 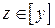 . Это значит, что
. Это значит, что 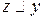 . Но
. Но 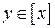 , значит
, значит  . Из транзитивности отношения
. Из транзитивности отношения 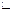 следует, что
следует, что 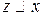 . Значит,
. Значит, 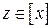 . Следовательно,
. Следовательно, 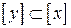 .
.
Пусть теперь 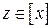 . Это значит, что
. Это значит, что 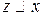 . Поскольку
. Поскольку 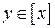 , имеем
, имеем  . Из симметричности отношения
. Из симметричности отношения 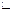 следует, что
следует, что 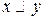 , а тогда по транзитивности отношения
, а тогда по транзитивности отношения 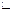 получим, что
получим, что 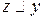 . Это значит, что
. Это значит, что 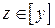 . Следовательно,
. Следовательно, 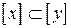 .
.
Если 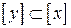 и
и 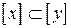 , то
, то 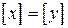 .
.
3. Если 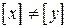 , то
, то 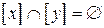 .
.
Доказательство. Предположим, что утверждение неверно. Это значит, что найдется 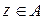 , принадлежащий как классу эквивалентности
, принадлежащий как классу эквивалентности 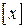 , так и классу эквивалентности
, так и классу эквивалентности 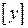 . Тогда
. Тогда 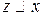 и
и 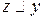 . Из симметричности и транзитивности отношения
. Из симметричности и транзитивности отношения 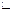 следует, что
следует, что 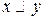 . Тогда по свойству 2
. Тогда по свойству 2 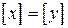 , что противоречит условию. Полученное противоречие доказывает справедливость утверждения.
, что противоречит условию. Полученное противоречие доказывает справедливость утверждения.
 Определение 2.3. Рассмотрим множество A . Пусть
Определение 2.3. Рассмотрим множество A . Пусть 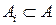 ,
, 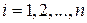 . Множество
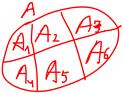
. Множество 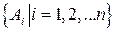 называется разбиением множества A, если оно удовлетворяет условиям:
называется разбиением множества A, если оно удовлетворяет условиям:
1) 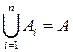 ,
,
2) 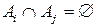 , при
, при 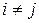 .
.
Примеры. 1) Множества четных чисел и нечетных чисел составляют разбиение множества целых чисел.
2) Множество всех людей живущих на Земле можно представить в виде разбиения на подмножества, состоящих из людей определенного года рождения.
Теорема 2.1. Классы эквивалентности множества A составляют разбиение множества A.
Доказательство. Рассмотрим множество 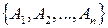 – классов эквивалентности множества A, порожденных некоторым отношением эквивалентности. Докажем, что множество
– классов эквивалентности множества A, порожденных некоторым отношением эквивалентности. Докажем, что множество 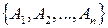 является разбиением множества A.
является разбиением множества A.
1) Докажем, что 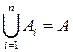 . Пусть
. Пусть 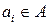 и
и 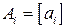 ,
, 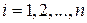 . Очевидно, что
. Очевидно, что 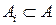 ,
, 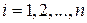 , следовательно,
, следовательно, 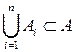 .
.
Пусть 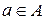 . Тогда найдется такой класс эквивалентности
. Тогда найдется такой класс эквивалентности 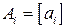 (ошибка - нужно убрать индекс у мал. а), что
(ошибка - нужно убрать индекс у мал. а), что
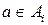 . Значит,
. Значит, 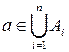 , и тогда
, и тогда 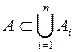 .
.
Если 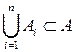 и
и 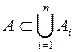 , то
, то 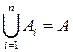 .
.
2) Условие 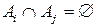 при
при 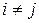 следует из свойства 3 классов эквивалентности. Теорема доказана.
следует из свойства 3 классов эквивалентности. Теорема доказана.
Определение 2.4. Рассмотрим множество A и 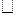 – отношение эквивалентности на A. Пусть
– отношение эквивалентности на A. Пусть 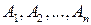 – классы эквивалентности, порожденные отношением
– классы эквивалентности, порожденные отношением  . Множество
. Множество 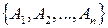 называется фактор-множеством множества A по отношению эквивалентности
называется фактор-множеством множества A по отношению эквивалентности  , и обозначается A│~.
, и обозначается A│~.
Примеры. 1) Пусть A – множество студентов потока. Рассмотрим бинарное отношение  на множестве A, определяемое следующим образом:
на множестве A, определяемое следующим образом: 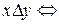 студенты x и y учатся в одной группе. Тогда, как было установлено выше, отношение
студенты x и y учатся в одной группе. Тогда, как было установлено выше, отношение  является отношением эквивалентности. При этом элементами фактор-множества A│Δ, порожденного отношением
является отношением эквивалентности. При этом элементами фактор-множества A│Δ, порожденного отношением  , являются группы данного потока.
, являются группы данного потока.
2) Рассмотрим множество целых чисел Z и введем на этом множестве бинарное отношение  :
: 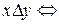 разность
разность 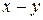 является четным числом. Отношение
является четным числом. Отношение  , очевидно, является отношением эквивалентности. Фактор-множество Z│Δ состоит из двух элементов – множества четных чисел и множества нечетных чисел.
, очевидно, является отношением эквивалентности. Фактор-множество Z│Δ состоит из двух элементов – множества четных чисел и множества нечетных чисел.
Продолжим изучение свойств бинарных отношений.
4. Бинарное отношение  на множестве A называется антисимметричным, если из условия
на множестве A называется антисимметричным, если из условия 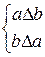 следует, что
следует, что 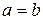 .
.
Пример. Пусть 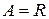 . Рассмотрим бинарное отношение
. Рассмотрим бинарное отношение 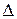 на множестве R, определяемое следующим образом:
на множестве R, определяемое следующим образом: 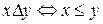 . Тогда бинарное отношение
. Тогда бинарное отношение  антисимметрично. Действительно,
антисимметрично. Действительно, 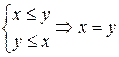 .
.
5. Бинарное отношение  на множестве A называется асимметричным, если из условия
на множестве A называется асимметричным, если из условия 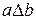 следует, что
следует, что 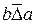 , т. е.
, т. е. 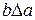 – неверно.
– неверно.
Пример. Пусть 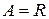 . Рассмотрим бинарное отношение
. Рассмотрим бинарное отношение 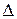 на множестве
на множестве 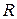 , определяемое следующим образом:
, определяемое следующим образом: 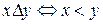 . Тогда бинарное отношение
. Тогда бинарное отношение  aсимметрично. Действительно, если
aсимметрично. Действительно, если 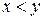 , то, очевидно, что
, то, очевидно, что 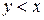 – неверно.
– неверно.
6. Бинарное отношение  на множестве A называется антирефлексивным, если не существует такого элемента
на множестве A называется антирефлексивным, если не существует такого элемента 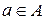 , что
, что 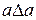 .
.
Пример. В предыдущем примере бинарное отношение  , очевидно, антирефлексивно.
, очевидно, антирефлексивно.
Определение 2.5. Бинарное отношение, обладающее свойствами рефлексивности, антисимметричности и транзитивности называется отношением нестрогого порядка.
Примеры. 1) Пусть 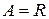 . Рассмотрим бинарное отношение
. Рассмотрим бинарное отношение 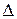 на множестве
на множестве 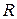 , определяемое следующим образом:
, определяемое следующим образом: 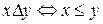 . Тогда, очевидно, бинарное отношение
. Тогда, очевидно, бинарное отношение  является отношением нестрогого порядка.
является отношением нестрогого порядка.
2) Пусть A – множество всех подмножеств множества 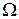 . Введем бинарное отношение
. Введем бинарное отношение  на множестве A:
на множестве A: 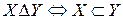 . Докажем, что
. Докажем, что  – отношение нестрогого порядка. Действительно, для любого множества X справедливо
– отношение нестрогого порядка. Действительно, для любого множества X справедливо 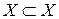 , следовательно, бинарное отношение
, следовательно, бинарное отношение  рефлексивно. Если
рефлексивно. Если 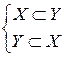 , то,
, то, 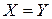 , следовательно, бинарное отношение
, следовательно, бинарное отношение  антисимметрично. И, наконец, если
антисимметрично. И, наконец, если 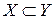 и
и 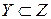 , то, очевидно,
, то, очевидно, 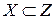 , следовательно, бинарное отношение
, следовательно, бинарное отношение  транзитивно.
транзитивно.
Определение 2.6. Бинарное отношение, обладающее свойствами антирефлексивности и транзитивности называется отношением строгого порядка.
Примеры. 1) Пусть 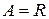 . Рассмотрим бинарное отношение
. Рассмотрим бинарное отношение 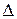 на множестве
на множестве 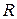 :
: 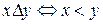 . Тогда, очевидно, бинарное отношение
. Тогда, очевидно, бинарное отношение  является отношением строгого порядка.
является отношением строгого порядка.
2) Пусть A – множество всех людей на Земле. Определим бинарное отношение  на множестве A :
на множестве A : 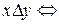 человек x является потомком человека y. Тогда бинарное отношение
человек x является потомком человека y. Тогда бинарное отношение  является отношением строгого порядка. Действительно, никакой человек не может быть собственным потомком, это означает, что бинарное отношение
является отношением строгого порядка. Действительно, никакой человек не может быть собственным потомком, это означает, что бинарное отношение  антирефлексивно. Если человек x является потомком человека y, а человек y является потомком человека z, то x является также потомком z. Это означает, что бинарное отношение
антирефлексивно. Если человек x является потомком человека y, а человек y является потомком человека z, то x является также потомком z. Это означает, что бинарное отношение  транзитивно.
транзитивно.
Замечание. Отношение строгого порядка обладает свойством асимметричности. Докажем это утверждение. Рассмотрим множество A и отношение строгого порядка  на этом множестве. Предположим, что
на этом множестве. Предположим, что  не обладает свойством асимметричности. Это означает, что в множестве A найдутся такие элементы x и y, что
не обладает свойством асимметричности. Это означает, что в множестве A найдутся такие элементы x и y, что 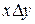 и
и 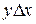 . Тогда по транзитивности
. Тогда по транзитивности  получим, что
получим, что 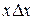 , а это противоречит антирефлексивности
, а это противоречит антирефлексивности  . Полученное противоречие доказывает, что сделанное предположение неверно, следовательно,
. Полученное противоречие доказывает, что сделанное предположение неверно, следовательно,  асимметрично.
асимметрично.
Определение 2. 7. Множество, на котором задано отношение порядка (строгого или нестрогого) называется частично упорядоченным.
В частично упорядоченном множестве могут существовать пары элементов, не связанные отношением порядка.
Примеры. 1) Пусть 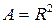 . Введем на множестве
. Введем на множестве 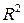 бинарное отношение
бинарное отношение 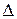 :
: 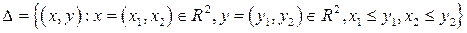 . Тогда
. Тогда 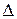 – отношение нестрогого порядка на
– отношение нестрогого порядка на 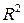 . Следовательно, множество
. Следовательно, множество 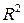 является частично упорядоченным. При этом в множестве
является частично упорядоченным. При этом в множестве 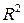 имеются элементы, не находящиеся в отношении
имеются элементы, не находящиеся в отношении 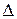 , например,
, например, 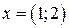 и
и 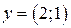 .
.
2) Пусть A – множество всех подмножеств множества 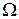 . Введем бинарное отношение
. Введем бинарное отношение  на множестве A:
на множестве A: 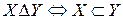 . Выше было доказано, что
. Выше было доказано, что  – отношение нестрогого порядка. Таким образом, множество A частично упорядочено. Очевидно, что в множестве A содержатся подмножества, не находящиеся в отношении
– отношение нестрогого порядка. Таким образом, множество A частично упорядочено. Очевидно, что в множестве A содержатся подмножества, не находящиеся в отношении  .
.

Определение 2.8. Множество A называется совершенно упорядоченным (или линейно упорядоченным), если на нем задано отношение порядка, причем любые два элемента этого множества связаны этим отношением.
Примеры. 1) Множестводействительных чисел R с введенным на нем отношением нестрогого порядка  :
: 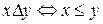 является, очевидно, совершенно упорядоченным.
является, очевидно, совершенно упорядоченным.
2) Рассмотрим конечное множество 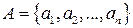 , состоящее из различных элементов. На множестве A всегда можно ввести такое отношение порядка, что множество A будет совершенно упорядоченным. Например, если
, состоящее из различных элементов. На множестве A всегда можно ввести такое отношение порядка, что множество A будет совершенно упорядоченным. Например, если 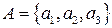 , то с бинарным отношением
, то с бинарным отношением 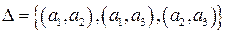 , являющимся строгом порядком, множество A будет совершенно упорядоченным.
, являющимся строгом порядком, множество A будет совершенно упорядоченным.
Дата добавления: 2021-02-19; просмотров: 896;











