Независимого возбуждения

Одним из основных электромеханических преобразователей энергии в регулируемом электрическом приводе является двигатель постоянного тока независимого возбуждения (ДПТ НВ).

Схема подключения ДПТ НВ к источнику постоянного напряжения U представлена на рис. 2.32.

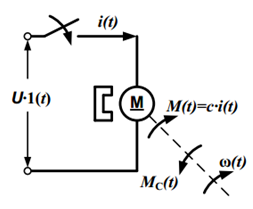
Рис. 2.32. Схема подключения ДПТ НВ к источнику постоянного напряжения

Схема замещения якорной цепи ДПТ НВ показана на рис. 2.33.

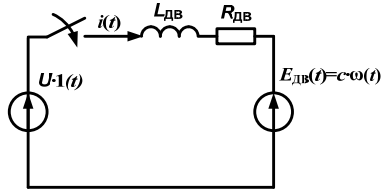
Рис. 2.33. Схема замещения якорной цепи ДПТ НВ

При составлении математической модели ДПТ НВ примем следующие допущения. Считаем, что реакция якоря полностью скомпенсирована (в реальном ДПТ всегда есть компенсационная обмотка либо добавочные полюса), поток возбуждения постоянен, а активное сопротивление якорной цепи не изменяется во время работы двигателя.

Запишем дифференциальное уравнение электрического равновесия якорной цепи двигателя (рис. 2.32):

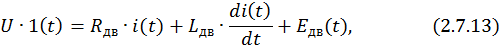
где R_ДВ – суммарное активное сопротивление последовательно включенных обмотки якоря и добавочных полюсов в горячем состоянии (при t = =75 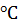); L_ДВ – суммарная индуктивность якорной цепи; E_ДВ(t) – противо-ЭДС двигателя; U⋅1(t) – напряжение, приложенное к якорной цепи; i(t) – ток якорной цепи. Уравнение механического равновесия двигателя –

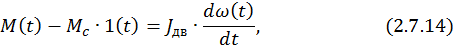
где M(t) – электромагнитный момент ДПТ НВ; M_C⋅1(t) – момент сопротивления нагрузки; J_ДВ – суммарный момент инерции, приведенный к валу двигателя; ω(t) – скорость двигателя.

Учитывая, что 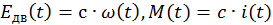, где c – коэффициент ЭДС и момента ДПТ НВ, запишем СДУ:

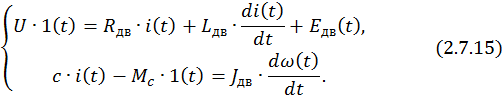
СДУ в нормальной форме Коши –

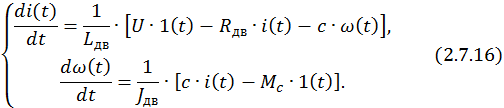
В матричном виде

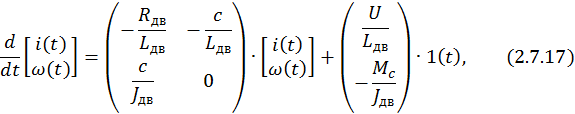
где 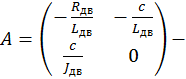матрица коэффициентов перед переменными состояния; 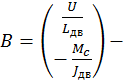вектор свободных членов СДУ;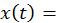

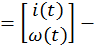вектор переменных состояния.

Из полученной математической модели ДПТ НВ видно, что переменными состояния в нем являются скорость вала и ток в якорной цепи. Эти переменные состояния соответственно связаны с массой вала и индуктивностью обмотки якоря, т.е. с механической и электрической инерционностями двигателя.