Сложение взаимно перпендикулярных колебаний

Рассмотрим теперь систему, совершающую колебания вдоль осей x и y. Моделью такой системы может служить груз массой m на двух перпендикулярных пружинах (рис. 7.8).

Запишем уравнение траектории движения материальной точки в параметрической форме, где параметром является время t:

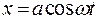
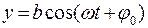, (7.25)

Для удобства начальная фаза колебаний вдоль оси х взята равной нулю: 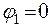, а начальная фаза колебаний вдоль оси y: , тогда разность фаз: .

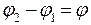Исключим время t из этих соотношений:

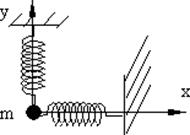
Рис. 7.8.

(7.26)

Получим уравнение

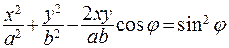(7.27)

Рассмотрим сложение взаимно перпендикулярных колебаний при различных начальных фазах:

1.j = 0, 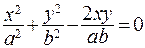, или ,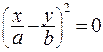

получим уравнение прямой:

(7.28)

Результирующее колебание происходит по прямой. Расстояние от конечной точки прямой до начала координат изменяется со временем по закону:

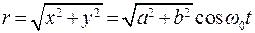(7.29)

Амплитуда колебаний:

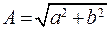(7.30)

2. 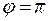, , 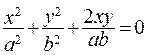или запишем это уравнение в виде

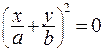(7.31)

Колебания происходят вдоль прямой .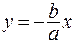

В рассмотренных случаях результирующее колебание называется линейно поляризованным.

3. 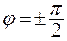. Получим уравнение эллипса, приведенного к координатным осям:

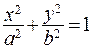(7.32)

При различных амплитудах ( ) траектория представляет собой эллипс, при одинаковых амплитудах ( ), траекторией является окружность.

Если 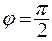, то движение материальной точки происходит по часовой стрелке (рис. 7.9). Уравнение траектории:

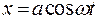
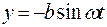, (7.33)

Если 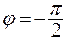, то точка движется против часовой стрелки. Уравнение траектории:

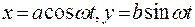(7.34)

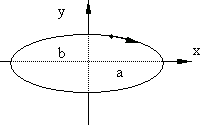
Рис. 7.9.

Результирующее колебание является эллиптически поляризованным при и поляризованным по кругу при .