Затухающие колебания

Уравнение затухающих колебаний:

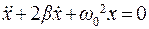(7.35)

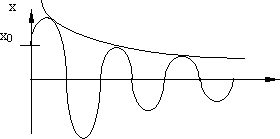
Рис. 7.10.

имеет решение:

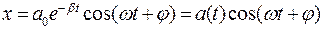(7.36)

где 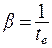- коэффициент затухания; t_e - время уменьшения амплитуды в e раз: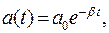 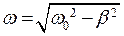- частота колебаний.

Графически полученное решение представлено на рис. 7.10.

Декремент затухания:

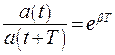(7.37)

Логарифмический декремент затухания:

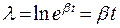(7.38)

Вынужденные колебания

Уравнение вынужденных колебаний

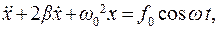(7.39)

его решение получим в виде

где ;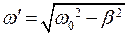

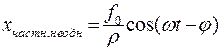- частное решение неоднородного дифференциального уравнения;

;

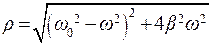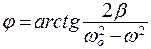(7.40)

Амплитуда колебаний зависит от частоты вынуждающей силы:

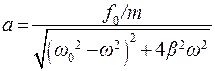(7.41)

При резонансной частоте, 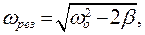амплитуда возрастает

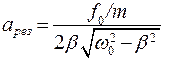(7.42)

Если сопротивление среды отсутствует, то коэффициент затухания 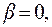отсюда следует 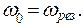Амплитуда при резонансе стремится к бесконечности (рис. 7.13).

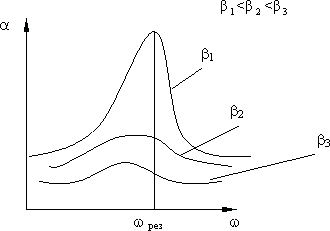
Рис. 7.11.

На рис. 7.11 представлены резонансные кривые для различных значений параметра b

Контрольные вопросы:

1. Классификация колебательного движения.

2. Собственные колебания. Затухающие колебания.

3. Вынужденные колебания. Параметрические колебания.

4. Параметры колебательного движения: амплитуда, частота.

5. Параметры колебательного движения: период, фаза.

6. Уравнения гармонических колебаний.

7. Математический маятник.

8. Оборотный маятник.