Отверстие незатопленное

Для определения скорости и расхода жидкости, вытекающей из отверстия, применяем уравнение Бернулли. Принимаем сечение 1-1 по свободной поверхности жидкости в резервуаре, второе сечение 2-2 проведем через сжатое сечение струи С-С. Плоскость сравнения 0-0 проводим через центр сжатого сечения параллельно свободной поверхности (см. рис. 6.1). Истечение жидкости осуществляется в атмосферу.

Напишем уравнение Бернулли для сечений 1-1 и 2-2:

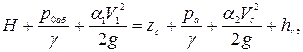(6.2)

где 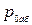- абсолютное давление на свободной поверхности жидкости в резервуаре; 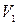, 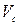- средние скорости в соответствующих сечениях; 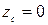; 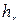- потери напора на участке от сечений 1-1 к 2-2.

Согласно формуле Вейсбаха

,

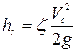где 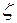- коэффициент местных сопротивлений отверстия.

Принимаем .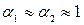

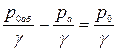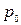( - избыточное давление в сечении 1-1).

Следовательно,

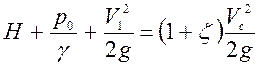. (6.3)

Скоростью 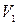, в резервуаре можно пренебречь, считая что площадь его поперечного сечения .

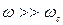Величину 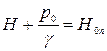назовем приведенным напором.

Тогда

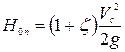. (6.4)

Отсюда скорость в сжатом сечении

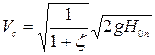. (6.5)

Введем следующее обозначение:

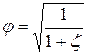, (6.6)

uде 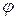- коэффициент скорости истечения.

Окончательно формула скорости истечения будет иметь следующий вид:

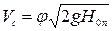. (6.7)

Для частного случая, когда 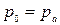, т.е. резервуар сообщается с атмосферой,

.

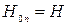В результате скорость

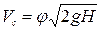. (6.8)

Для идеальной жидкости потери напора 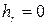и 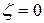, а коэффициент скорости .

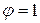Теоретическая скорость истечения в этом случае

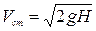. (6.9)

Зависимость (6.9) - формула Торричелли, полученная им в 1643 г. на основании опытов при определении скоростей истечения в случае разных напоров .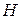

Физический смысл коэффициента 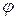заключается в том, что он выражает отношение действительной скорости 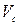к теоретической скорости ( ).

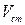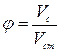Зная скорость истечения, можно найти расход Q. При условии, что ,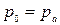

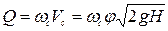. (6.10)

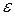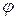Назовем произведение двух коэффициентов и коэффициентом расхода отверстия :

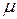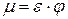. (6.11)

Тогда выражение для расхода при истечении через отверстие будет

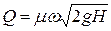. (6.12)

Коэффициент расхода учитывает как степень сжатия, так и потери напора 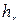, характеризующиеся коэффициентом местных сопротивлений .

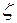Коэффициент 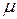определяется опытным путем, и его значение изменяется в диапазоне 0,59 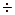0,64. Как правило, для предварительных расчетов принимается .

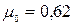Следует отметить, что при истечении через малые отверстия за сжатым сечением происходит деформация поперечного сечения струи. Форма деформированного сечения отличается от формы сечения отверстия, из которого происходит истечение. Такое явление носит название инверсии струи, которая происходит из-за поверхностного натяжения жидкости. Например, при истечении из круглого отверстия поперечное сечение струи имеет форму эллипса, а для квадратного сечения струя приобретает крестообразную форму.