Истечение жидкости через отверстие при постоянном напоре

Выведем формулы скорости и расхода жидкости при истечении через малое отверстие с острыми кромками (рис. 10.1).

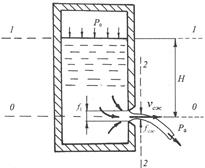
Рис.10.1 Истечение жидкости через малое отверстие в атмосферу

Опытами установлено, что сжатое сечение струи находится от внутренней поверхности резервуара на расстоянии около половины диаметра отверстия.

Высоту уровня жидкости в резервуаре Н над центром отверстия называют геометрическим напором.

Проведем плоскость сравнения 2-2 через центр сжатого сечения струи.

Напишем уравнение Д. Бернулли для сечений 1-1 и 2-2

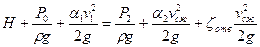(10.2)

где 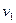– скорость подхода жидкости к отверстию в резервуаре; 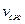– средняя скорость течения в сжатом сечении; 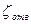– коэффициент местного сопротивления при истечении через отверстие.

Коэффициент Кориолиса 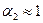, 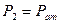на уровне 0 – 0.

Из уравнения расхода известно, что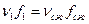

Решая систему уравнений (10.2) и уравнения расхода относительно скорости в сжатом сечении получим:

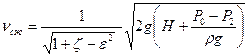(10.3)

Обозначим величину

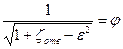(10.4)

Величину 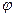называют коэффициентом скорости.

С учетом введенного обозначения

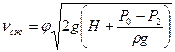(10.5)

По опытным данным ,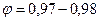

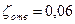
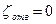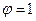Для идеальной жидкости и . Для открытого бака,

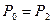, отсюда можно получить:

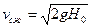(10.6)

Это уравнение называется формулой Торичелли. Оно показывает, что скорость в начале вытекающей струи равна скорости свободного падения тела, упавшего с высоты .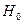

Расход жидкости определится как произведение скорости истечения на площадь сжатого сечения струи

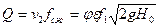(10.7)

Величину 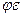обозначают через 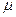и называют коэффициентом расхода.

Таким образом, расход жидкости, вытекающей через отверстие, определяют по формуле

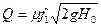(10.8)

При точных измерениях размеров сжатого сечения струи установлено, что при совершенном сжатии струи 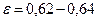. В этом случае 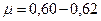. В общем же случае коэффициент расхода 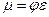зависит от условий сжатия.