Истечение через прямоугольное отверстие и водослив

Рассмотрим истечение через большое (широкое) прямоугольное отверстие (рис. 7.7).

Верхняя кромка отверстия расположена на глубине H₁, а нижняя – на глубине H₂ от свободной поверхности жидкости. Ширина отверстия (перпендикулярно плоскости чертежа) – b.

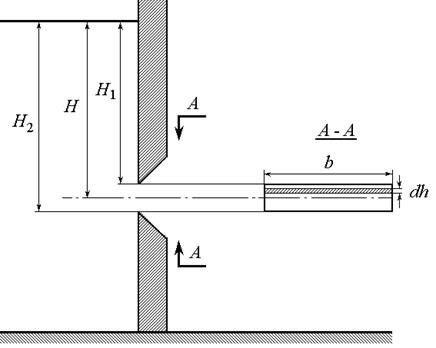
Рис. 7.7

Элементарный расход через малый прямоугольный элемент площади можно записать как:

.

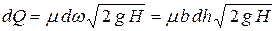Для того чтобы найти расход через все отверстие, проинтегрируем выражение для элементарного расхода по h в пределах от H₁ до H₂,считая µ постоянным.

.

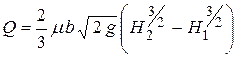Это формула для расхода через прямоугольное отверстие. Но эта формула, как правило, не имеет самостоятельного значения. Она важна как исходная для получения формулы для прямоугольного водослива с тонкой стенкой. Такой водослив получается, если в рассмотренной схеме положим H₁ = 0 (рис. 7.8).

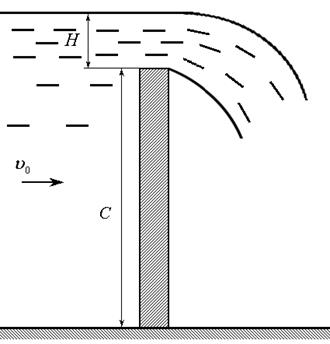
Рис. 7.8

Обозначим 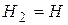. Назовем величину 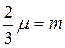коэффициентом расхода для водослива. Тогда:

.

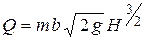(7.4)

Значение m в первом приближении можно получить, принимая как для малого круглого отверстия, µ = 0,62. Тогда m ≈ 0,42.

В наших рассуждениях мы не учитывали скорость подхода воды к водосливу 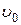и высоту водослива С. С учетом этих величин можно уточнить формулу (7.4).