Истечение жидкости через малое круглое отверстие
В современной гидравлической аппаратуре имеется большое количество форсунок, жиклеров, дросселей и других элементов, работающих по типу отверстий в тонкой или толстой стенках. Поэтому для расчетов режимов работы элементов гидроаппаратуры необходимо изучение закономерностей таких течений.
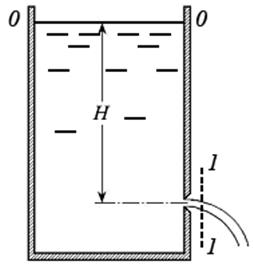
Рис. 7.1
Рассмотрим несколько случаев истечения жидкости из резервуаров через отверстия или насадки (короткие трубки разной формы) в атмосферу или в пространство, заполненное той же жидкостью. В этих случаях в процессе истечения запас потенциальной энергии, которым обладает жидкость в резервуаре, превращается (с определенными потерями) в кинетическую энергию струи или капель. Основной вопрос при рассмотрении таких случаев истечения – определение скорости истечения и расхода жидкости для различных форм отверстий и насадок.
Рассмотрим большой резервуар с жидкостью (рис. 7.1), свободная поверхность которой находится при атмосферном давлении pатм. На глубине H от поверхности жидкости в стенке резервуара устроено малое круглое отверстие диаметром d0. Отверстие можно считать малым, если его диаметр значительно (в несколько раз) меньше напора H. В случае, когда толщина стенки меньше диаметра отверстия, стенка считается тонкой.
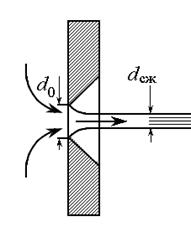
Рис. 7.2
Частицы жидкости внутри резервуара приближаются к отверстию из всего прилегающего объема, двигаясь ускоренно. У кромки отверстия струя отрывается от стенки и несколько сжимается (рис. 7.2). Сжатие происходит потому, что движение плавно переходит от разнонаправленного (в резервуаре) к осевому (в истекающей струе). Цилиндрическую форму струя принимает на расстоянии 0,5 – 0,7 d 0 от стенки, в дальнейшем сжатия не происходит.
Степень сжатия характеризуется коэффициентом сжатия ε, равным отношению площади сжатой струи к площади отверстия.
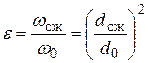 .
.
Если отверстие малое, то, как показывают исследования, коэффициент сжатия не зависит от напора перед отверстием и его размера.
Для определения необходимых нам величин – расхода и скорости в струе – запишем уравнение Бернулли для движения жидкости, выбрав в качестве одного сечения 0–0 плоскость свободной поверхности резервуара, а в качестве другого сечения 1–1 – сжатое сечение струи:
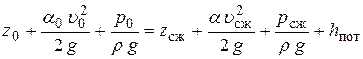 .
.
Так как площадь свободной поверхности резервуара много больше площади отверстия, то можно считать, что уровень свободной поверхности не снижается и 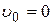 , то есть истечение происходит при постоянном напоре H. Давление на свободной поверхности резервуара и на поверхности сжатой струи равно атмосферному:
, то есть истечение происходит при постоянном напоре H. Давление на свободной поверхности резервуара и на поверхности сжатой струи равно атмосферному:
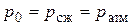 .
.
В качестве плоскости сравнения выберем ось струи, тогда
z0 = H, zсж = 0.
Потери напора определятся как:
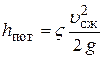 ,
,
здесь 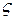 – коэффициент сопротивления отверстия.
– коэффициент сопротивления отверстия.
Учитывая все это, получим
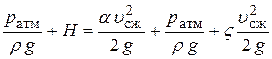 ,
,
откуда
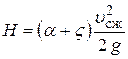 .
.
Тогда скорость 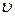 сж
сж
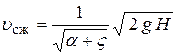 .
.
Введем обозначение:
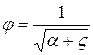 . .
| (7.1) |
Параметр φ называется коэффициентом скорости.
Получаем
 . .
| (7.2) |
Найдем расход жидкости через отверстие:
 .
.
Используя определение коэффициента сжатия, получаем
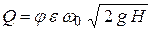 .
.
Величина 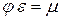 – это и есть коэффициент расхода. Тогда
– это и есть коэффициент расхода. Тогда
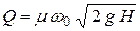 . .
| (7.3) |
Оценим численные значения коэффициентов, входящих в эти выражения.
Для развитого турбулентного течения в струе профиль скоростей в сжатом сечении близок к прямоугольному и 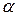 = 1. Тогда
= 1. Тогда
 .
.
Коэффициент сопротивления отверстия можно принять равным 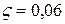 , а коэффициент сжатия струи – ε = 0,64. Отсюда получим φ = 0,96 и µ = 0,62.
, а коэффициент сжатия струи – ε = 0,64. Отсюда получим φ = 0,96 и µ = 0,62.
Заметим, что при истечении без сжатия струи µ = φ.
Выражения (7.2) и (7.3) и служат для решения основной задачи расчета – определения скорости и расхода при истечении жидкости через малое круглое отверстие в тонкой стенке.
Обратим внимание на следующие особенности смысла коэффициентов скорости φ и расхода µ.
В случае истечения из отверстия идеальной жидкости трение и завихрения отсутствуют, поэтому 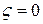 , а
, а 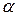 = 1, следовательно, из (7.1) получаем φ = 1, и скорость истечения идеальной жидкости по (7.2) будет
= 1, следовательно, из (7.1) получаем φ = 1, и скорость истечения идеальной жидкости по (7.2) будет
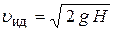 .
.
Тогда при течении реальных жидкостей из формулы (7.2) получим
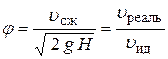 ,
,
то есть коэффициент скорости есть отношение реальной скорости истечения к скорости идеальной жидкости. Действительная скорость истечения всегда несколько меньше идеальной из-за сопротивления, значит, коэффициент скорости всегда меньше единицы.
Из формулы (7.3) получаем для коэффициента расхода выражение
 .
.
Заметим, что 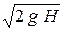 – это скорость истечения идеальной жидкости, а произведение ее на площадь отверстия ω0 дает расход жидкости, который был бы, если бы отверстие не имело сопротивления, и не было бы сжатия. На самом деле сжатие будет даже и у идеальной жидкости. Но тем не менее получаем, что коэффициент расхода есть отношение реального расхода к некому теоретическому идеализированному расходу при течении без сжатия и без сопротивления.
– это скорость истечения идеальной жидкости, а произведение ее на площадь отверстия ω0 дает расход жидкости, который был бы, если бы отверстие не имело сопротивления, и не было бы сжатия. На самом деле сжатие будет даже и у идеальной жидкости. Но тем не менее получаем, что коэффициент расхода есть отношение реального расхода к некому теоретическому идеализированному расходу при течении без сжатия и без сопротивления.
 .
.
Действительный расход также всегда меньше теоретического и, следовательно, коэффициент расхода всегда меньше единицы вследствие влияния двух факторов – сжатия струи и наличия сопротивления.
Все безразмерные коэффициенты, введенные в рассмотрение:
· сжатия ε;
· сопротивления 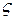 ;
;
· скорости φ;
· расхода µ
зависят от типа отверстия или насадка, от сил тяжести и поверхностного натяжения, а также от основного критерия гидродинамического подобия – числа Re. Для малого отверстия ( 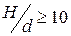 ) влияние сил тяжести практически не проявляется. Заметное влияние сил поверхностного натяжения наблюдается только при малых напорах.
) влияние сил тяжести практически не проявляется. Заметное влияние сил поверхностного натяжения наблюдается только при малых напорах.
Получим формулы траектории струи, вытекающей из отверстия, то есть формулы, связывающие горизонтальную (абсциссу x) и вертикальную (ординату y) координаты частицы, движущейся в центре тяжести струи. Как известно из кинематики движущейся точки
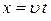 ;
; 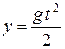 ,
,
кроме того, при истечении из отверстия 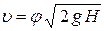 .
.
Проведем некоторые преобразования
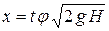 ;
; 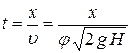 ;
; 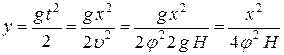 ;
;
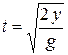 ;
; 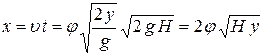 ;
;
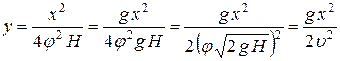 ;
; 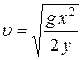 .
.
Таким образом, получены следующие зависимости для расчета траектории струи
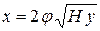 ;
; 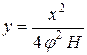 ;
; 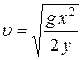 .
.
Дата добавления: 2017-04-05; просмотров: 2843;











