Нечеткие числа и интервалы доверия

Нечеткие числа

Предположим имеется число А, которое назовем "центральным измеренным значением". Это число получено посредством субъективных измерений (оценок). Поскольку нет уверенности, что число А является точным, т.е. А - неточное число, введем некоторую ошибку DА, которая может быть положительной или отрицательной. Таким образом, А±DА будет представлять подмножество возможных значений от А-DА до А+DА, где А - есть центральное значение и DА - положительное отклонение. Обозначим нечеткое число большой курсивной буквой и тремя значениями:

А=(А-DА,А,А+DА)

Рассмотрим операции на нечетких числах.

Сумма нечетких чисел. Пусть А=(А-DА,А,А+DА) и В=(В-DВ,В,В+DВ) - два нечетких числа. Сумма двух нечетких чисел, обозначаемая знаком ‘Å‘, определятся так:

АÅВ=(А-DА,А,А+DА)Å(В-DВ,В,В+DВ)=(А+В-DА-DВ,А+В,А+В+DА+DВ).

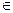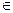Числа А и В являются вещественными числами, т.е. А R, B R, в то время как DА и DВ будут неотрицательными вещественными числами, т.е. DАÎR и DВÎR.

Пример.

А=(4,5,6) с D5=1

В=(1,3,5) с D3=2

То есть А=(5-1,5,5+1)

В=(3-2,3,3+2)

АÅВ=(3+5-1-2,5+3,5+3+1+2)=(5,8,11)

Очевидно, что сумма нечетких чисел коммутативна и ассоциативна.

Разность нечетких чисел, обозначаемая знаком -, определяется следующим образом:

А(-)В = (А-DА,А,А+DА)(-)(В-DВ,В,В+DВ) =

= (А-DА-(В+DВ)),А-В,А+DА-(В-DВ)) =

= (А-В-DА-DВ,А-В,А-В+DА+DВ).

Откуда следует

D(А-В)=DА+DВ

т.е. отклонения в операции разность суммируются, когда остаются центральные значения.

Пример:

А=(4,5,6) с D5=1

В=(1,3,5) с D3=2

А(-)В=(5-3-1-2,5-3,5-3+1+2)=(-1,2,5) с D2=3

Если для точных чисел

А-А=0

то для нечетких чисел следующее:

А(-)А = (А-DА,А,А+DА)-(А-DА,А,А+DА) =

= (0-2DА,0,0+2DА) =

= (-2DА,0,2DА), D0=2DА.

Не только результат вычитания не равен (0,0,0), т.е. 0, но даже отклонение D0=2DА.

Определим дополнение А.

А^- =(0,0,0)(-)(А-DА,А,А+DА)=(-А-DА,-А,-А+DА).

АÅА^- =(А-DА,А,А+DА)Å(-А-DА,-А,-А+DА)=(-2DА,0,2DА).

Умножение нечетких чисел в R⁺ и R. Умножение нечетких чисел в R выполняется сложнее, чем в R⁺. Рассмотрим вначале эту операцию в R.

АÄВ = (А-DА,А,А+DА)Ä(В-DВ,В,В+DВ) =

= [(А-DА)*(В-DВ),А*В,(А+DА)*(В+DВ) =

= [(А*В-В*DА-А*DВ+DА*DВ),А*В,(А*В+В*DА+А*DВ+DА*DВ)]

Нетрудно заметить, что следует различать отклонение слева (D_l) от отклонения справа (D_r).

D_l(А*В)=В*DА+А*DВ-DА*DВ

D_r(А*В)=В*DА+А*DВ+DА*DВ

Для большего удобства запишем

А=(А-D_lА,А,А+D_rА)

В=(В-D_lВ,В,В+D_rВ)

АÄВ = (А*В-В*D_lА-А*D_lВ+D_lА*D_lВ,А*В,А*В+В*D_rА+А*D_rВ+D_rА*D_rВ);

D_l(А*В)=В*D_lА+А*D_lВ-D_lА*D_lВ,

D_r(А*В)=В*D_rА+А*D_rВ+D_rА*D_rВ,

Пример:

А=(3,8,9), D_l8=5, D_r8=1

В=(4,5,7), D_l5=1, D_r5=2

АÄВ=(5*8-88*1-5*5+5*1,5*8,5*8+8*2+5*1+1*2)=(12,40,63).

Формула вычисления операции умножения двух нечетких чисел в R является несколько более сложной, чем в R⁺.

Пример:

А = (-2,3,5), D_l3=5, D_r3=2

В = (-3,-1,4), D_l(-1)=2, D_r(-1)=5

В начале требуется вычислить АÄВ, используя их собственные числа. Нижнее значение произведения будет иметь вид:

MIN[(-2)*(-3), 5*(-3), (-2)*(4), (5)*(4)] =

= MIN(6, -15, -8, 20) = -15.

Таким же образом вычисляется верхнее значение:

MAX(6, -15, -8, 20)=20

Имеем

АÄВ=(-15, -3, 20), D_l(-3)=12, D_r(-3)=23.

Теперь в R получим общую формулу. Положим

D={(А-D_lА)*(В-D_lВ),(А-D_lА)*(В+D_rВ),(А+D_rА)*(В-D_lВ),

(А+D_rА)*(В+D_rВ)}.

MIN(kÎD) - даст минимальное значение, k

MAX(kÎD) - даст максимальное значение, k

A*B - даст центральное значение.

Применим эти формулы к нашему примеру:

D={(3-5)*(-1-2),(3-5)*(-1+5),(3+2)*(-1-2),(3+2)*(-1+5)}=

={6,-8,-15,20}.

MIND=-15, MAXD=20.

AÄB=(-15,-3,20).

Очевидно, что операция умножения коммутативна и дистрибутивна в R.

Деление нечетких чисел. Вначале определим обратное число А в R следующим образом:

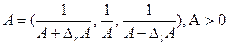
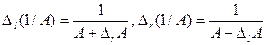
Заметим, что обратное число в R не всегда определено. Действительно пусть А=(-3,2,5). Обратное число для (-3) будет (-1/3), для 2 - 1/2, для 5 - 1/5. Принимая все обратные числа от -1/3 до 1/5, мы проходим через число 0,обратное значение которого от -¥ до ¥, поэтому невозможно получить нечеткое число в форме (A-D_lA,A,A+D_rA). И мы ограничились положительными числами.

Теперь рассмотрим операцию деления в R⁺.

A(:)B = (A-D_lA,A,A+D_RA)(:)(B-D_lB,B,B+D_rB) =

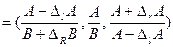
Откуда предполагается, что B>0 (и следовательно D_lB<B). Для R⁺₀ можно всегда написать:

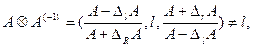
за исключением, если A=(A,A,A)=A.

Также интересно рассмотреть дистрибутивность, существующую между операциями Å и Ä.

Дистрибутивность для реальных чисел не имеет места:

АÅ(ВÄС)=(АÅВ)Ä(АÅС).

Что касается дистрибутивности чисел в R , то имеем:

АÄ(ВÅС)=(АÄВ)Å(АÄС).

Переход от нечетких чисел к относительным. Допустим, что D_lА и D_rА достаточно малы по сравнению с А. Тогда D_lА называют "абсолютной ошибкой слева" и D_rА - "абсолютной ошибкой справа" по отношению к А.

Если D_lА и D_rА достаточно малы, то пренебрегают D_lА*D_rА перед D_lА и D_rА, что позволяет упростить различные формулы и, в частности, формулу произведения:

АÄВ=(А*В-В*D_lА-А*D_lВ,А*В,А*В+В*D_rА+А*D_rВ),

D_lА, D_rА<<А, D_lВ, D_r<<В

В теории ошибок вводится понятие "относительной ошибки", т.е. D_lА/А и D_rА/А, называемые соответственно "относительной ошибкой слева" и "относительной ошибкой справа" по отношению А. Это понятие особенно полезно для операций произведения и деления, для которых имеем:

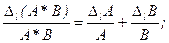
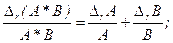
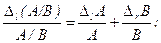
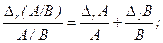
В обоих случаях относительные ошибки всегда суммируются.

В категории ошибок отклонения слева и справа часто принимаются равными и относительные отклонения D_lА/D_rА выражаются через них.

Интервалы доверия

Рассмотрим некоторую величину Х из R, о которой известно, что она имеет "неточное" значение. Существует много ситуаций, для которых с уверенностью можно утверждать, что Х³a₁ и Х³a2,и a₁, a₂ из R, т.е. Х принадлежит сегменту А=[a₁,a₂] из R. Теперь предположим, что существует некоторый вероятностный закон, с помощью которого устанавливается принадлежность элементов Х из [a₁,a₂]. Поэтому говорят, что А=[a₁,a₂] является интервалом доверия. Нужно отметить, что можно рассматривать интервалы, открытые слева или справа или с обеих сторон. Далее мы будем рассматривать закрытые с двух сторон интервалы или сегменты.

Нетрудно убедиться, что интервал или область доверия должны быть выпуклыми. Выпуклость области доверия можно определить следующим образом: Пусть А - область доверия в Rⁿ, n=1,2,3... . Если две точки Х⁽¹⁾,Х⁽²⁾ из А, то любая точка Х' из [Х⁽¹⁾, Х⁽²⁾] принадлежит А.

Рассмотрим классические операции, относящиеся к интервалам доверия. Сложение интервалов доверия. Пусть А=[a₁,a₂] из R, B=[b1,b2] из R и предположим, что X из [a1,a2] и Y из [b1,b2]. Каким является интервал доверия, которому принадлежит XÅY? Ответ достаточно прост:

a₁£x£a₂, b1£x£b2

и поэтому a₁+b1£x+y£a₂+b2,т.о. x+yÎa₁+b1,a₂+b2].

Сложение записывается так: АÅВ=[a₁,a₂]Å[b1,b2]=[a₁+b1,a₂+b2].

Пример 1:

А=[-2,7],B=[4,5]

A+B=[2,12].

Вычитание интервалов доверия. Поменяем знаки у второго интервала и воспользуемся результатом операции сложения.

a₁£x£a₂,-b2£-y£-b1

выполняется a₁-b2£x-y£a₂-b1, т.е. x-yÎ[a₁-b2, a₂-b1].

Операция вычитания записывается следующим образом:

А(-)В=[a₁, a₂]-[b1,b2]=[a₁-b2,a₂-b1].

Пример 2:возьмем данные из примера 1

A(-)B=[-7,3]

Умножение интервалов доверия. Oперация умножения AÄB=[a₁,a₂]*[b1,b2] даст следующие результаты

Таблица 1

Эти результаты получаются из общей формулы:

AÄB=[MIN(a₁*b2,a2*b1,a₁*b1,a2*b2),

MAX(a₁*b2,a2*b1,a₁*b1,a2*b2)]

Пример 3.

AÄB=[-2,7]Ä[4,5]=[-10,35].

Прежде чем осуществить деление, рассмотрим результат обратного действия.

Имеется шесть случаев:

1) 0<a₁£a2 : [a₁,a₂] ^(-1)=[1/a2,1/a1]

2) 0=a₁<a2 : [a₁,a₂] ^(-1)=[1/a2,¥]

3) 0=a₁=a2 : единственная точка ¥

4) a₁£a2<0 : [a₁,a₂] ^(-1)=[1/a2,1/a1]

5) a₁<a2=0 : [a₁,a₂] ^(-1) =(-¥,1/a₁]

6) a₁£0£a2 : [a₁,a₂] ^(-1) = (-¥,1/a₁]È[1/a2,¥)

Отсюда следует что [a₁,a2]Ä[a₁,a2]^(-1)¹1.

Пример 4.

A^(-1)=[-2,7]^(-1)=[MIN(-1/2,1/7),MAX(-1/2,1/7)]=[-1/2,1/7].

Деление. Если В^(-1) есть интервал доверия, то операция деление записывается так:

A(:)B=AÄB^(-1).

Умножение на число К.

При K*А=[MIN(K*a₁,K*a2),MAX(K*a₁,K*a2)].

При К=-3 и А=[-2,7] К*А=[-21,6].

Минимум. Используем символ "Ç" в качестве минимума

A(Ç)B=[a1,a2](Ç)[b1,b2]=

=[MIN(a₁,b1),MIN(a2,b2)]=[a₁Çb1,a2Çb2].

Максимум. Используем символ "È" в качестве максимума:

A(È)B=[a₁,a2](È)[b1,b2]=

=[MAX(a₁,b1),MAX(a2,b2)]=[a₁Èb1,a2Èb2]

Легко проверить, что операции АÇB И AÈB коммутативны, ассоциативны и дистрибутивны.

Сравнение интервалов доверия. Интервалы доверия А из R не образуют как R общий, а частичный порядок. Для перехода от частичного порядка к общему необходимо установить произвольно критерий и если одного недостаточно, то перейти к другому. Возьмём в качестве первого критерия сумму абсцисс экстремумов или абсцисс середины интервала.

l([a₁,a₂]) =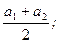

Следовательно А>B, если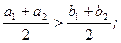

если a₁ + a₂ = b₁ + b₂, то нужно взять другой критерий, например A>B, если a₂ > b₂.