Нечеткие подмножества
Пусть Е есть множество, А - подмножество Е, т.е. АÌЕ. Принадлежность любого элемента х подмножеству А можно выразить с помощью характеристической функции или функции принадлежности m(х), значения которой указывают, является ли (да или нет) х элементом А:
mA(х)=1 если хÎА
mA(х)=0 если хÏА.
Пример:
Пусть Е={х1,х2,х3,х4,х5} и пусть А={х1,х3,х5}. Степень принадлежности каждого элемента Е множеству А выражается характеристической функцией: mA(х1)=1; mA(х2)=0; mA(х3)=1; mA(х4)=0; mA(х5)=1.
Это позволяет представить А посредством всех элементов множества Е и соответствующих им значений функцией принадлежности:
А={(х1,1),(х2,0),(х3,1),(х4,0),(х5,1)}.
Предположим теперь, что характеристическая функция для элементов множества А вместо того, чтобы принимать только значения 0 или 1 могут принимать любое значение аÎ[0,1], т.е. mA(х)=аÎ[0,1].
В соответствии с этим элемент х2 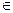 Е может не принадлежать А(mA(x)=0), может быть элементом А в небольшой степени (mA(x) близко к 0), может более или менее принадлежать А (mA(х)»0,5), может в значительной степени быть элементом А (mA близко к 1) или, наконец, может быть элементом А (mA(х)=1).
Е может не принадлежать А(mA(x)=0), может быть элементом А в небольшой степени (mA(x) близко к 0), может более или менее принадлежать А (mA(х)»0,5), может в значительной степени быть элементом А (mA близко к 1) или, наконец, может быть элементом А (mA(х)=1).
Математический объект, определяемый выражением А={(х1¦0,2),(х2¦0,4),(х3¦1),(х4¦0),(х5¦0,8)}, где хi - элемент универсального множества Е, а число после вертикальной черты дает значение характеристической функции для этого элемента, будем называть нечетким подмножеством множества Е. Нечеткое подмножество будем обозначать полужирной буквой с символом ‘_’ под ней:
Принадлежность элементов нечеткому подмножеству можно обозначать так:

 Ì E или AÌE
Ì E или AÌE
Приведем примеры нечетких подмножеств.
На рис. 12.1 представлена граница нечеткого подмножества, внутри которой указаны значения характеристической функции для элементов этого подмножества.
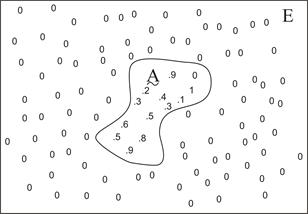
Рис. 12.1. Нечеткое подмножество
На рис. 12.2 представлено нечеткое подмножество с помощью его функции принадлежности.
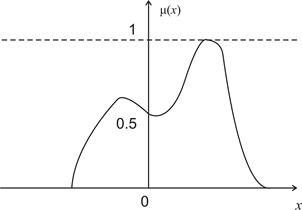
Рис. 12.2. Представление нечеткого подмножества с помощью функции принадлежнасти
Дадим строгое определение понятия нечеткого подмножества, введенного Л. Заде. Пусть Е есть множество, счетное или нет, и х - элемент Е. Тогда нечетким подмножеством А множества Е называется множество упорядоченных пар
{(x| 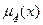 }, "xÎE
}, "xÎE
где 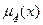 - степень принадлежности х в
- степень принадлежности х в  . Таким образом, если
. Таким образом, если 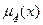 принимает свои значения во множестве М значений функции принадлежности, то можно сказать, что х принимает значение в М посредством
принимает свои значения во множестве М значений функции принадлежности, то можно сказать, что х принимает значение в М посредством 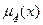 .
.
Следовательно,
x ~® M
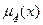
Множество М называют множеством принадлежностей.
Рассмотрим несколько примеров:
1) нечеткое подмножество чисел х, приблизительно равных данному действительному числу n, где nÎR (R - множество действительных чисел);
2) нечеткое множество целых чисел близких к 0;
3) пусть а - действительное число и х - небольшое положительное приращение а; тогда а+х образуют нечеткое подмножество во множестве действительных чисел.
Пример.
Пусть N - множество целых чисел
N = {-8,-5,-3,0,1,2,4,6,9}
Рассмотрим нечеткое подмножество чисел по абсолютной величине
близких к 0.
А = {(-8¦0), (-5¦0,5), (-3¦0,6), (0¦1), (1¦0,9), (2¦0,8), (4¦0,6), (6¦0,3), (9¦0)}
Здесь значения 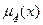 , где х=-8,-5,-3... , задаются, конечно, субъективно.
, где х=-8,-5,-3... , задаются, конечно, субъективно.
Эту формулу можно записать в виде:
-8Î  , -5 Î
, -5 Î  , -3 Î
, -3 Î  , ...
, ...
0 0.5 0.6
Операции над нечеткими множествами. Рассмотрим различные операции теории обычных множеств применительно к нечетким подмножествам, а также введем новые операции для последних. Пусть Е - множество и М=[0,1] - множество принадлежностей,  и
и  - два нечетких подмножества из Е.
- два нечетких подмножества из Е.
Равенство. Два нечетких подмножества  и
и  равны (обозначается
равны (обозначается  =
=  ) тогда и только тогда, когда (A=B) Û ("xÎE:
) тогда и только тогда, когда (A=B) Û ("xÎE: 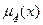 =
= 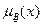 ).
).
Если найдется по крайней мере один такой элемент х из Е, что равенство 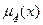 )¹
)¹ 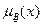 не удовлетворяется, то будем говорить, что
не удовлетворяется, то будем говорить, что  и
и  не равны и обозначать
не равны и обозначать  ¹
¹ 
Пересечение. Пересечение двух нечетких подмножеств, обозначаемое  и
и  определяют как наибольшее нечеткое подмножество, содержащееся одновременно в
определяют как наибольшее нечеткое подмножество, содержащееся одновременно в  и
и  . (AÇB)=("xÎE:
. (AÇB)=("xÎE: 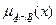 )=MIN(
)=MIN( 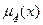 ),
), 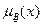 ).
).
Пример.
Е={х1,х2,х3,х4,х5}, M=[0,1].
 ={(х1¦0,1),(х2¦0,5),(х3¦1),(х4¦0),(х5¦0,8)}.
={(х1¦0,1),(х2¦0,5),(х3¦1),(х4¦0),(х5¦0,8)}.
 ={(х1¦0,6),(х2¦1),(х3¦0,4),(х4¦0,7),(х5¦0,8)}.
={(х1¦0,6),(х2¦1),(х3¦0,4),(х4¦0,7),(х5¦0,8)}.
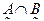 ={(х1¦0,1),(х2¦0,5),(х3¦0,4),(х4¦0),(х5¦0,8)}.
={(х1¦0,1),(х2¦0,5),(х3¦0,4),(х4¦0),(х5¦0,8)}.
На рис. 12.3 представлено графически пересечение двух нечетких подмножеств.
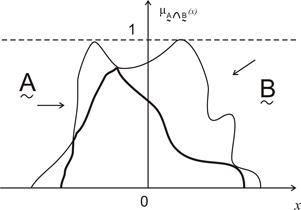
Рис. 12.3. Пересечение двух нечетких подмножеств
Объединение. Объединение двух нечетких подмножеств  и
и  ,
, 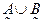 , определим как наименьшее нечеткое подмножество, которое содержит как А, так и В:
, определим как наименьшее нечеткое подмножество, которое содержит как А, так и В:
( 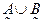 )=("xÎE:
)=("xÎE: 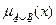 )=MAX(
)=MAX( 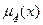 ),
), 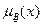 )
)
Вернувшись к примеру, получим
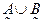 ={(х1¦0.6),(х2¦1),(х3¦1),(х4¦0.7),(х5¦0.8)}.
={(х1¦0.6),(х2¦1),(х3¦1),(х4¦0.7),(х5¦0.8)}.
На рис. 12.4 представлено графически объединение двух нечетких подмножеств.
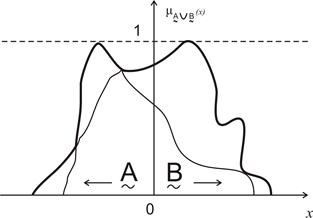
Рис. 12.4. Объединение двух нечетких подмножеств
Дополнение. Будем говорить, что  и
и  два нечетких подмножества Е дополняют друг друга, если
два нечетких подмножества Е дополняют друг друга, если
"xÎE: 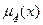 =1-
=1- 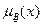 ).
).
Это обозначается так:
B=ùA или A=ùB
Пример:
Е = {х1,x2,x3,x4,x5}, M=[0,1].
A = {(х1¦0.15),(х2¦0.45),(х3¦0),(х4¦0.75),(х5¦1)}.
B = {(х1¦0.88),(х2¦0.55),(х3¦1),(х4¦0.25),(х5¦0)}.
Тогда очевидно ùA=B
На рис. 12.5 графически представлено дополнение нечеткого подмножества А.
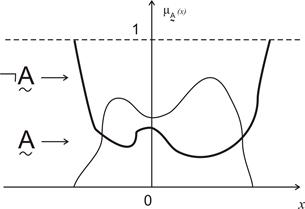
Рис. 12.5. Дополнение нечеткого подмножества
Включение. Будем говорить, что  содержится в
содержится в  , если
, если
"xÎE: 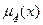 )£
)£ 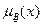
и обозначать  Ì
Ì  .
.
Строгое включение соответствует случаю, когда, по крайней мере, одно неравенство строгое и обозначается
Пример:
Пусть Е = {х1,х2,х3}, M=[0,1].
 = {(х1¦0,8),(х2¦0,6),(х3¦0,4)}.
= {(х1¦0,8),(х2¦0,6),(х3¦0,4)}.
 = {(х1¦0,5),(х2¦0,4),(х3¦0,1)}.
= {(х1¦0,5),(х2¦0,4),(х3¦0,1)}.
Имеем  Ì
Ì  , так как 0.5<0.8; 0.4<0.6; 0.1<0.4.
, так как 0.5<0.8; 0.4<0.6; 0.1<0.4.
Дизъюнктивная сумма. Дизъюнктивная сумма двух нечетких подмножеств определяется в терминах объединений и пересечений следующим образом:
 Å
Å  = (
= (  Çù
Çù  )È(ù
)È(ù  Ç
Ç  )
)
Пример.
 = {(х1¦0.1),(х2¦0.5),(х3¦1),(х4¦0),(х5¦0.8)}.
= {(х1¦0.1),(х2¦0.5),(х3¦1),(х4¦0),(х5¦0.8)}.
 = {(х1¦0.6),(х2¦1),(х3¦0.4),(х4¦0.7),(х5¦0.8)}.
= {(х1¦0.6),(х2¦1),(х3¦0.4),(х4¦0.7),(х5¦0.8)}.
ù  = {(х1¦0.9),(х2¦0.5),(х3¦0),(х4¦1),(х5¦0.2)}.
= {(х1¦0.9),(х2¦0.5),(х3¦0),(х4¦1),(х5¦0.2)}.
ù  = {(х1¦0.4),(х2¦0),(х3¦0.6),(х4¦0.3),(х5¦0.2)}.
= {(х1¦0.4),(х2¦0),(х3¦0.6),(х4¦0.3),(х5¦0.2)}.
 Çù
Çù  = {(х1¦0.1),(х2¦0),(х3¦0.6),(х4¦0),(х5¦0.2)}.
= {(х1¦0.1),(х2¦0),(х3¦0.6),(х4¦0),(х5¦0.2)}.
ù  Ç
Ç  = {(х1¦0.6),(х2¦0.5),(х3¦0),(х4¦0.7),(х5¦0.2)}.
= {(х1¦0.6),(х2¦0.5),(х3¦0),(х4¦0.7),(х5¦0.2)}.
 Å
Å  = {(х1¦0.6),(х2¦0.5).
= {(х1¦0.6),(х2¦0.5).
Разность определяется соотношением
 -
-  =
=  Çù
Çù 
Используя данные примера, получим
AÇùB = {(х1¦0,1),(х2¦0),(х3¦0.6),(х4¦0),(х5¦0.2)}.
В общем случае  -
-  ¹
¹  -
- 
Перемещение. Операция перемещения изменяет значения на величину l. При l>0
производится перемещение функции вправо, а при l<0 - влево.
Следовательно
"xÎE, 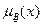 ¹
¹ 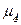 (x-l), lÎR
(x-l), lÎR
На рис. 12.6 графически представлено перемещение.
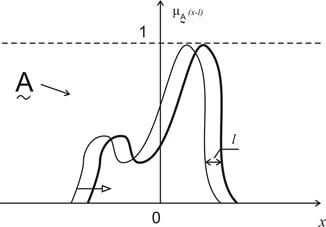
Рис. 12.6. Операция перемещения
Нормализация. Операция осуществляется в соответствии со следующей формулой:
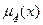
"xÎE, 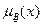 = --------------
= --------------
MAX 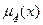
На рис. 12.7 графически представлен результат операции нормализации.
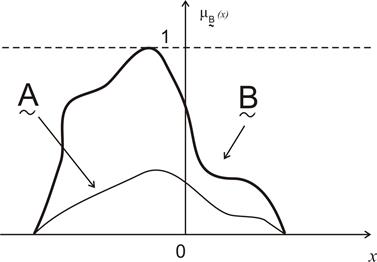
Рис. 12.7. Операция нормализации
Уплотнение. Операция осуществляется в соответствии со следующей формулой:
"xÎE, ( 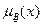 )k, k>1.
)k, k>1.
На рис.5.10 графически представлен результат операции уплотнения.
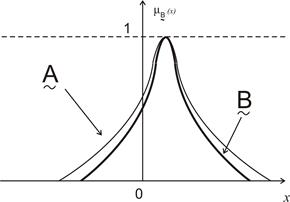
Рис. 5.10. Операция уплотнения
Растяжение. Операция осуществляется в соответствии со следующей формулой:
xÎE, 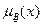 = (
= ( 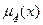 )k, 0<k<1.
)k, 0<k<1.
На рис. 12.8 графически представлен результат операции растяжения.
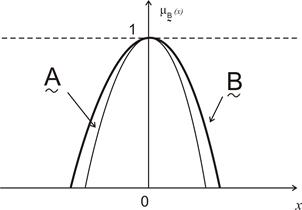
Рис. 12.6. Операция растяжения
Нечеткие отношения
Пусть Р прямое произведение n подмножеств A1,...,An, P=A1x...xAn и М его множество принадлежностей. Нечетное n-арное отношение определяется как нечёткое подмножество Р0 принимающее свои значения в М.
Пример.
Пусть Х={х1,х2,х5} и Y={y1,y2,y3,y4}, М=[0,1]. Следующая операция представляет собой 2-арное нечёткое отношение
| R | y1 | y2 | y3 |
| x1 | 0.2 | 0.5 | |
| x2 | 0.4 | 0.9 |
Далее будем использовать символы È - для обозначения максимума относительно элемента или переменной х, Ç - для обозначения минимума относительно элемента или переменной х. Так
m1(x)=È m(x,y)=MAXm(x,y)
y y
m2(x)=È m(x,y)=MINm(x,y)
y y
Пересечение двух отношений R и L обозначается RЗL и определяется выражением
mRÇL(x,y)= mR(x)ÇmL(x)=MIN(mR(x),mL(x))
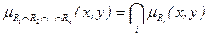
Если R1,...,Rn - отношение, то
Результат пересечения обозначим R=ÇRi.
| R1 | y1 y2 y3 |
| x1 | 0.2 0.5 1 |
| x2 | 0 0.4 0.9 |
| R2 | y1 y2 y3 |
| x1 | 0.3 0.6 0.9 |
| x2 | 0.1 0.4 0.8 |
| R3 | y1 y2 y3 |
| x1 | 0.2 0.5 0.9 |
| x2 | 0 0.4 0.8 |
Объединение двух отношений R и L обозначается RÈL или R+L и определяется выражением
mRÈL(x,y)=mR(x,y)ÈmL(x,y)=MAX(mR(x,y),mL(x,y))
Если R1,...,Rn - отношение, то
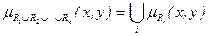
Результат пересечения обозначим RÈRi.
i
Пример.
| Y1 | y1 y2 y3 |
| x1 | 0.2 0.5 1 |
| x2 | 0 0.4 0.9 |
| Y2 | y1 y2 y3 |
| x1 | 0.3 0.6 0.9 |
| x2 | 0.1 0.4 0.8 |
| Y3 | y1 y2 y3 |
| x1 | 0.3 0.6 1 |
| x2 | 0.1 0.4 0.9 |
Алгебраическое произведение R*L двух отношений R и L определяется выражением
mR*L(x,y)=mR(x,y)*mL(x,y)
Знак "*" в правой части этого выражения обозначает обычное умножение
Свойство дистрибутивности для операций È и * имеет следующий вид:
RЗ(LUB) = (RЗB)U(RЗB)
RU(LЗB) = (RUL)З(RUB)
R*(LUB) = (R*L)U(R*B)
R*(LЗB) = (R*L)З(R*B)
Алгебраическая сумма двух отношений R и L обозначается R+L и определяется следующим выражением:
mR+L(x,y)=mR(x,y)+mL(x,y)-mR(x,y)*mL(x,y)
Знак "*" обозначает обычное умножение, а знак "+" - обычное сложение.
Дополнение отношения R (обозначается 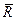 ) есть такое отношение, что
) есть такое отношение, что
m(x,y)ÎXxY: 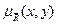
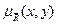 =1-mR(x,y)
=1-mR(x,y)
Пример.
| R | y1 y2 y3 |
| x1 | 0.2 0.5 1 |
| x2 | 0.1 0.4 0.9 |
| R | y1 y2 y3 |
| x1 | 0.3 0.6 0.9 |
| x2 | 0.1 0.4 0.8 |
Дизъюнктивная сумма двух отношений R и L обозначается R+L и определяется выражением RÅL=(RЗL)U(RЗL).
| R | y1 y2 y3 |
| x1 | 0.2 0.5 1 |
| x2 | 0 0.4 0.9 |
| L | y1 y2 y3 |
| x1 | 0.3 0.6 0.9 |
| x2 | 0.1 0.4 0.8 |
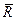
| y1 y2 y3 |
| x1 | 0.8 0.5 0 |
| x2 | 1 0.4 0.1 |
| y1 y2 y3 |
| x1 | 0.7 0.4 0.1 |
| x2 | 0.9 0.6 0.2 |
| RÈL | y1 y2 y3 |
| x1 | 0.2 0.4 0.1 |
| x2 | 0 0.4 0.2 |
| RÇL | y1 y2 y3 |
| x1 | 0.3 0.5 0 |
| x2 | 0.1 0.4 0.1 |
| RÅL | y1 y2 y3 |
| x1 | 0.3 0.5 0.1 |
| x2 | 0.1 0.4 0.2 |
Обычное отношение R, ближайшее к нечёткому отношению R определяется выражением
ì 0, Если mR(x,y)<0.5
mR (x,y)= 1, Если mR(x,y)<0.5
î 0 или 1, Eсли mR(x,y)=0.5
Это определение пригодно для любых полных множеств Х и У, образующих ХхУ, где хÎХ, уÎУ.
| R | y1 y2 y3 |
| x1 | 0.2 0.5 1 |
| x2 | 0 0.4 0.9 |
| R | y1 y2 y3 |
| x1 | 0 0 1 |
| x2 | 0 0 1 |
Композиция двух нечётких отношений. Пусть R1 и R2 два нечётких отношения R1ÌXxY, R2ÌYxZ.
Композиция max-min двух нечётких отношений R1 и R2 обозначаются R1oR2 и определяются выражением
mRoL(x,y)=È(mR(x,y)ÇmL(x,y))=MAX(MIN(mR(x,y),mL(x,y)))
y y y
Пример.
| R1 | y1 y2 y3 |
| x1 | 0.2 0.5 1 |
| x2 | 0 0.4 0.9 |
| R2 | z1 z2 z3 |
| y1 | 0.9 0.4 0.2 |
| y2 y3 | 0 0.4 0.9 0.8 0.6 0.3 |
| R1oR2 | z1 z2 z3 |
| y1 | 0.9 0.4 0.2 |
| y2 y3 | 1 0.5 0.1 0.5 0.6 0.3 |
Пусть (x,z)=(x1,z1)
MIN(mR1(x1,y1),mR2(y1,z1))=MIN(0.1,0.9)=0.1
MIN(mR1(x1,y2),mR2(y2,z1))=MIN(0.4,1)=0.4
MIN(mR1(x1,y3),mR2(y3,z1))=MIN(0.7,0.8)=0.7
MAX(MIN((mR1(x1,yi),mR2(yi,z1)))=MAX(0.1,0.4,0.7)=0.7
yi
Пусть теперь (x,z)=(x1,z2)
MIN(mR1(x1,y1),mR2(y1,z2))=MIN(0.1,0.4)=0.1
MIN(mR1(x1,y2),mR2(y2,z2))=MIN(0.4,0.5)=0.4
MIN(mR1(x1,y3),mR2(y3,z2))=MIN(0.7,0.6)=0.6
MAX(MIN((mR1(x1,yi),mR2(yi,z2)))=MAX(0.1,0.4,0.6)=0.6
И т.д. Окончательный результат представлен в таблице выше.
Заключение.
Поскольку математическая логика опирается на точные формализмы и не содержит нечёткостей, то для того чтобы сделать модель более адекватной реальной действительности требуется использовать теорию и методы представления и обработки чёткостей. Булева алгебра всегда будет полезна там, где требуется точность вычисления. Благодаря Заде она получила широкое толкование с точки зрения теории множеств. С совершенно другой позиции, на основе n-местной логики Пост (1921), Лукашевич (1937) и Мойзл (1940) разработали теории, в которых имели место некоторые аспекты нечётких множеств.
Трудно указать пользователю метод обработки нечёткости, имеющейся в задаче. Адекватность того или иного метода можно оценить на конкретных примерах или благодаря эвристическим знаниям. Ещё недостаточно изучены методы, когда существует взаимосвязь или совокупность различных видов нечёткостей. Неясно, можно ли различать унифицированные методы обработки нечётких знаний различного типа. Здесь рассмотрено применение нечётких знаний в дедуктивных выводах. Интерес представляют и нечёткие знания в индуктивных выводах, в процессах обучения.
Теория обработки нечётких знаний по своей природе вполне соответствует потребностям современной экономики. Задачи управления предприятиями и макроэкономического анализа, в области бизнеса, финансов и банковского дела базируются на знаниях опыта экспертов и естественно они являются нечёткими. Многочисленные статьи, монографии, касающиеся применения теории нечёткостей, свидетельствуют об эффективности рассмотренных методов.
Упражнения
12.1. Для универсального множества Е={А,В,С,О,Е,Р,С}
и нечетких множеств
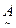 ={(
={( 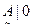 ), (
), ( 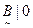 , 3), (
, 3), ( 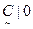 , 7), (
, 7), ( 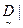 1), (
1), ( 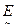 |0), (
|0), ( 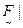 0, 2), (
0, 2), ( 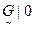 ,6)},
,6)},
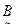 ={(
={( 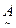 |0, 3), (
|0, 3), ( 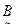 |1), (
|1), ( 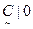 , 5), (
, 5), ( 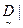 0. 8), (
0. 8), ( 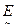 |1), (
|1), ( 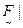 0, 5), (
0, 5), ( 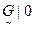 , 6)},
, 6)},
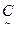 ={(
={( 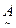 |1), (
|1), ( 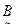 |0, 5), (
|0, 5), ( 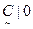 , 5), (
, 5), ( 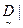 0, 2), (
0, 2), ( 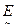 |0), (
|0), ( 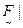 0, 2), (
0, 2), ( 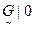 , 9)},
, 9)},
Найдите:
а) 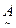 ∩
∩ 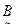 , б)
, б) 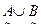 , в)(
, в)( 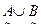 )∩С, , г)
)∩С, , г) 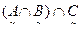 , д)
, д) 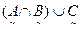 .
.
Дата добавления: 2016-10-26; просмотров: 3353;











