Нейроны и связи между ними
Основные компоненты искусственных нейронных сетей моделируют структуру мозга. Поэтому большая часть терминологии в этой области появилась из нейронауки, которая исследует мозг и память. В связи с этим рассмотрим основные компоненты мозга, чтобы облегчить понимание сущности блоков искусственной нейронной сети.
Компоненты мозга. Мозг состоит из нейронов, которые являются малыми единицами обработки информации. Нейроны получают вход либо из внешнего окружения, либо от других нейронов. Нейроны соединены в большую и сложную сеть. Она состоит из дендритов, которые передают сообщения через различные пути в сети. Дендриты можно себе представить как дороги или скоростные пути, связывающие различные города (нейроны).
Связь этой сети с некоторым нейроном называется синапсомили синоптической связью. В нашей “дорожной” терминологии синапс является связью, где скоростной путь входит в город. Когда много дорог ведет в город, то будет много связей в этом городе. Это случай со многими нейронами и синапсами. Синапс можно рассматривать как точку соединения, в которой принимаются сигналы дендритами. Нейроны имеют много таких точек соединения в сети. Нейронможет иметь до 10000 синапсов. Около 1011 нейронов участвуют примерно в 1015 передающих связях длиной в один метр и более. Уникальной способностью нейрона является прием, обработка и передача электрохимических сигналов по нервным путям. Дендритыидут от тела нервной клетки к другим нейронам, где они принимают сигналы в точках соединения, называемых синапсами. Принятые синапсом входные сигналы суммируются, причем одни входы стремятся возбудить нейрон, другие - воспрепятствовать его возбуждению. Когда суммарное возбуждение в теле нейрона превышает некоторый порог, нейрон возбуждается, посылая по аксону сигнал другим нейронам.
Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. В нейрон поступает некоторое множество входных сигналов из внешней среды или из других нейронов. Множество этих входных сигналов, обозначаемое вектором x1,...,xn, соответствует сигналам, приходящим в синапсы биологического нейрона. Каждый входной сигнал xi(i=1,...,n) умножается на соответствующий вес wi(i=1,...,n) и поступает на суммирующий блок Sxiwi. Вес wi соответствует “силе” одной биологической синоптической связи. Множество весов обозначается вектором W. Суммирующий блок, соответствующий телу биологического элемента, складывает взвешенные входы и создает выход, который будем обозначать NET (рис. 13.1). С использованием векторных обозначений NET=XW.
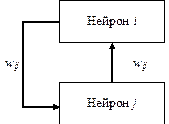 Рис. 13.1. Двунаправленная связь нейронов
Рис. 13.1. Двунаправленная связь нейронов
|
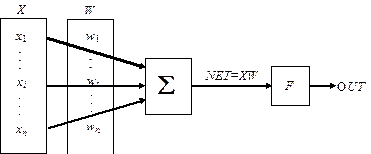 Рис. 13.2. Искусственный нейрон
Рис. 13.2. Искусственный нейрон
|
Нейроны соединяются в сеть путями, в которых выход одного нейрона служит в качестве входа другого нейрона. Эти пути, как правило, являются однонаправленными. Однако не запрещается использовать двунаправленную связь между двумя нейронами (рис. 13.2).
Одним из наиболее важных элементов при проектировании нейронных сетей является “сила” связи между двумя нейронами, обозначаемая весом этой связи wij. При двунаправленной связи между нейронами i и j, как правило, wij¹wji Позднее мы увидим, что область знаний формируется и хранится как множество значений этих весов и система обучается новым знаниям путем установления весов связей.
Рассмотрим более подробно входы и выходы нейронов. Нейрон i получает импульсы от n других нейронов, с которыми он соединен в сети. Поскольку нейрон i получает много входных импульсов, то его чистый вход равен:
| NETi=SwjiOUTj , | (13.) |
где j - все нейроны, соединенные с нейроном i.
В уравнении (13.1) вход i - это чистое значение всех взвешенных импульсов, входящих в нейрон. В некоторых сетях абсолютное значение весов ограничены интервалом от 0 до 1. Эта нормализация позволяет избежать больших значений на входе нейрона.
Активационные функции. Как мы уже говорили, сигнал NET преобразуется активационной функцией F, и нейрон выдает выходной сигнал OUT. Для этой цели могут использоваться различные функции, среди которых наиболее распространенными являются следующие: пороговая, сигнум, сигмоидальная, гиперболический тангенс, линейная, линейно-пороговаяфункции.
В пороговой функции нейрон остается неактивным до тех пор, пока его чистый вход не достигает порогового значения T. Когда этот порог достигнут, он возбуждается и посылает выходное дискретное значение, такое как 1. Пороговая функция может быть записана следующим образом:
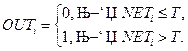
| (13.2) |
Когда в (13.2) порог T равен 0, то пороговая функция называется сигнум-функцией и записывается следующим образом:
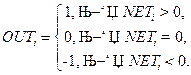
| (13.3) |
Пороговая функция наиболее точно моделирует нелинейную передаточную характеристику биологического нейрона и представляет нейронным сетям большие возможности.
Блок F может сужать диапазон изменений величины NET, так что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу. В этом случае F называется сжимающей функцией и в качестве такой функции может использоваться логистическая или сигмоидальная функция (рис. 13.3,в). Эта функция имеет следующий вид:
F(x)=1/(1+e-x)
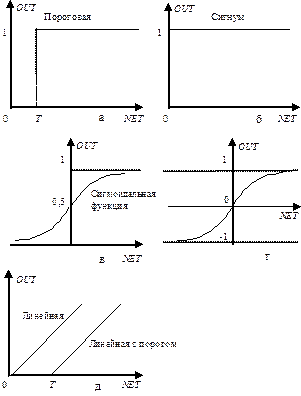 Рис. 13.3. Формы передаточных функций
Рис. 13.3. Формы передаточных функций
|
Таким образом,
OUT=1/(1+e-NET).
В этой функции при любых значениях NET множество значений OUT ограничено интервалом (0,1).
В общем, виде сигмоидальную функцию можно записать так:
| OUT=1/(1+eg×NET), | (13.4) |
где g - приращение. Например, g = 1/T, где T определено ранее как пороговое значение.
На рисунке 13.3,в показан вид такой функции.
Рассмотрим более детально суть активационной функции на примере логистической (сигмоидальной) функции. По аналогии с электронными системами активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления равен отношению приращения величины OUT к вызвавшему его небольшому приращению NET, т.е.
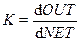 .
.
Он выражается наклонной кривой в зависимости от уровня возбуждения и изменяется от малых значений при больших отрицательных возбуждениях (кривая приближается к оси OX) до максимального значения при нулевом возбуждении и снова уменьшается при больших положительных возбуждениях. Сеть с такой функцией может успешно обрабатывать как слабые сигналы, которые она усиливает, так и сильные, которые нет необходимости усиливать.
При значениях, близких к нулю, логистическая функция
OUT=1/(1+e-NET)
принимает большие значения, которым соответствует больший коэффициент усиления, в то время как при больших отрицательных и положительных значениях NET логистическая функция принимает всё меньшее значение, т.е. требуется меньшее усиление сигналов. Таким образом, нейрон работает с большим усилением в широком диапазоне уровня входного сигнала.
Другой версией сигмоидальной передаточной функции является функция гиперболический тангенс, которая записывается в следующей форме:
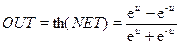
| (13.5) |
где U = g×NET. Эта функция имеет форму, подобную форме сигмоидальной функции с той разницей, что она симметрична относительно начала координат, и значения OUT находятся на интервале (-1,1). Когда u=0, то OUT=0. На рисунке 13.3,г изображена такая функция.
| OUT=g×NET | (13.6) |
Линейная передаточная функция имеет простую форму: OUT=g×NET Здесь g - системный параметр и в некоторых проектах значение g = 1.
Линейно-пороговая передаточная функция является другой формой линейной функции:
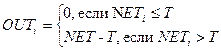
| (13.7) |
Эта функция допускает возбуждение нейрона только в случае достижения им порогового значения и выходное значение нейрона равно входному минус пороговое значение (рис. 13.3,е).
Графики передаточных функций на рисунке 13.3. показывают, что выход нейрона может быть двоичным (0 или 1) или принимать конечное значение на отрезках [0,1] или
[-1,1], а также значения, не ограниченные отрезком [0,1]. Выбор передаточной функции обычно связан с проектом нейронной сети для системы. В некоторых сетях разработчик свободен в выборе передаточной функции для сети.
Даже когда разработчик системы решил использовать нейронную сеть, в которой вид передаточной функции уже определен, то он должен определить параметры функции, такие как пороговое значение (T) в уравнениях (13.2) и (13.7) и переменную g в уравнениях (13.4) и (13.6). Определение передаточной функции и её параметров, разработчик проекта должен решить путем экспериментов с системой.
В рассмотренной простой модели искусственного нейрона отсутствуют многие свойства его биологического двойника. Например, в модели не учитываются задержки во времени, т.е. функции замедления (торможения), которые воздействуют на динамику системы. Входные сигналы сразу же порождают выходной сигнал. Не принимаются во внимание также воздействия функции синхронизации процессов, происходящих в биологическом нейроне, которые ряд исследователей считают решающими. Несмотря на эти ограничения, сети, построенные из этих нейронов, имеют свойства, сильно напоминающие биологическую систему.
Нейронные сети
Обработка знаний в нейронных сетях. Нейроны в сетях группируются по слоям. Имеются различные типы слоев. Например, входной слой состоит из нейронов, которые получают вход из внешней среды. Входной слой можно считать входной единицей нейронной сетевой системы. Выходной слой состоит из нейронов, которые связывают выход системы с пользователем или внешней средой.
Данные, вводимые во входной слой, отображают факты о некоторой проблеме принятия решения, например, о применении закладной на кредит. После ввода данных в сеть нейроны входного слоя возбуждаются и создают выход на другие слои системы. Обработка знаний в нейронной сети состоит из взаимодействия между слоями нейронов в системе. Эта обработка продолжается до удовлетворения некоторого условия, после чего нейроны выходного слоя возбуждаются и передают их выход во внешнюю среду.
Таким образом, проектирование связей между нейронами эквивалентно программированию системы для обработки входа и создания желаемого выхода. Проектирование нейронной сети состоит из:
· упорядочивания нейронов по слоям;
· определения связей между нейронами различных слоев, также как и между нейронами внутри слоя;
· решения о том, каким образом нейрон получает вход и как создает выход;
· определения силы связей внутри сети, чтобы узнать соответствующие значения весов путем использования контрольного набора данных.
Межслойные связи нейронов. В нейронной сети обычно имеется много связей между нейронами. Нейроны группируются по слоям и в каждом слое располагаются нейроны одного типа. Нейроны в слое могут иметь или не иметь связи между собой. Обычно во многих простых проектах нейроны одного слоя не имеют связей между собой. Нейроны одного слоя связаны с нейронами другого слоя. Имеются различные типы связей: полная связь, частичная связь, прямое распространение, двунаправленная, иерархическая и резонансная связи.
При полной связи каждый нейрон первого слоя связан с каждым нейроном второго слоя. При частичной связи слоев нейрон первого слоя не обязательно должен быть связан со всеми нейронами второго слоя.
При прямом распространении нейроны первого слоя посылают их выходы нейронам второго слоя, но не наоборот. При двунаправленной связи нейроны первого слоя связаны с нейронами второго, которые, в свою очередь, имеют связь с нейронами первого слоя. Связь прямого распространения и двунаправленная могут быть полностью или частично связанными.
Нейронная сеть может иметь один (однослойная) или много (многослойная) слоев. При иерархической связи нейроны нижнего слоя связаны только с нейронами следующего уровня. Если связь не иерархического типа, то нейроны одного слоя могут посылать свои выходы не только нейронам следующего слоя, но и другим слоям.
В резонансном типе связей два слоя имеют двунаправленную связь с дополнительным усложнением, что они продолжают передачу сообщений по связям некоторое число раз до выполнения некоторого условия.
Названные здесь типы межслойных связей используются в широко известных проектах нейронных сетей, которые мы рассмотрим в последующих разделах.
Однослойные нейронные сети. Простейшая нейронная сеть состоит из одного слоя нейронов и показана на рисунке 13.4. Вершины-круги слева служат лишь для распределения входных сигналов, не выполняют каких-либо вычислений и поэтому не считаются слоем. Элементы из множества входов X отдельными весами соединены с искусственными нейронами.
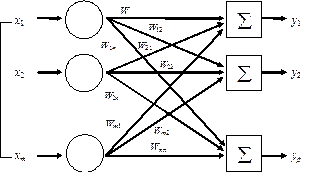 Рис. 13.4. Однослойная искусственная нейронная сеть
Рис. 13.4. Однослойная искусственная нейронная сеть
|
Веса удобно представить элементами матрицы wij, состоящей из m строк (число входов) и n столбцов (число нейронов). Например, w2,5 - это вес, связывающий второй вход с пятым нейроном. Таким образом, вычисление выходного вектора NET сводится к матричному умножению NET=XW, где NET и X - векторы-строки.
Многослойные нейронные сети. Искусственные нейронные сети с многочисленными слоями нейронов обладают большими возможностями и позволяют наиболее полно моделировать работу мозга. В последние годы были разработаны алгоритмы для их обучения. Выход одного слоя является входом другого слоя (рис. 13.5).
Многослойные нейронные сети не приводят к усложнению вычислений по сравнению с однослойной сетью лишь в том случае, если активационная функция между слоями будет линейной. Выход вычисляется путем умножения входного вектора на первую весовую матрицу с последующим умножением результирующего вектора на вторую весовую матрицу, т.е.
Y = (X×W1)×W2 = X×(W1×W2).
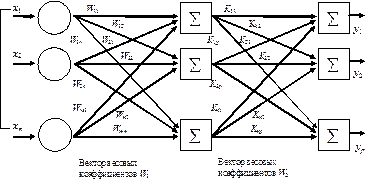 Рис. 13.5. Двухслойная искусственная нейронная сеть
Рис. 13.5. Двухслойная искусственная нейронная сеть
|
Ассоциативность умножения матриц показывает, что двухслойная линейная сеть эквивалентна одному слою с весовой матрицей, равной произведению двух весовых матриц. Следовательно, любая многослойная линейная сеть с весовыми векторами между слоями W1,...,Wn может быть заменена эквивалентной однослойной сетью с результатным выходным вектором Y=X×(W1×W2×,...,×Wn). Таким образом, расширение возможностей сетей по сравнению с однослойной сетью можно достигнуть путем использования нелинейной активационной функции.
До сих пор мы рассматривали только сети прямого распространения, в которых выход одного слоя используется в качестве входа последующих слоев. Такие сети получили большое распространение. Однако применяются сети и более общего вида - сети с обратными связями, в которых выход некоторого слоя используется в качестве входа того же слоя или предшествующих слоев. Сети без обратных связей не имеют памяти, их выход полностью определяется текущими входами и значениями весов. В сетях с обратными связями выход может определяться как текущим входом, так и предыдущими. По этой причине сети с обратными связями могут обладать свойствами, сходными с кратковременной человеческой памятью, где сетевые выходы частично зависят от предыдущих входов.
Персептроны
Персептрон- это первая нейронная сеть, разработанная Ф.Розенблатом в 1957 году с целью моделирования психологических аспектов мозга. Модель показала, что сеть может моделировать средства ассоциативной памяти мозга с их прямыми связями между слоями нейронов, которые способны обучаться, даже когда внешний вход имеет шумы и неточности.
На идеях персептрона был разработан компьютер, который распознавал изображения, в виде символов.
В дальнейшем Минский показал, что персептроны имеют ограничения, как в выполнении функций, так и в обучении. Поскольку в то время методы обучения многослойных сетей не были известны, то исследования в области нейронных сетей пришли в упадок. Только разработка методов обучения многослойных сетей оказала существенное влияние на возрождение интереса к исследованиям в этой области.
Персептрон имеет трехслойную, иерархическую, распространяющуюся вперед структуру с отсутствием связей между нейронами одного слоя. Первый слой является входным слоем, который получает внешние данные (рис. 13.6). Нейроны входного слоя посылают сигналы нейронам (всем или некоторому числу) следующего слоя. Весовые коэффициенты между первым и вторым слоем фиксированы и равны 1. Поэтому первый слой функционирует как входной буфер, который получает внешние импульсы и посылает их всем или некоторым нейронам второго слоя без изменения весовых коэффициентов. Поскольку весовые связи между первым и вторым слоем фиксированы, то, естественно, здесь отсутствует элемент обучения.
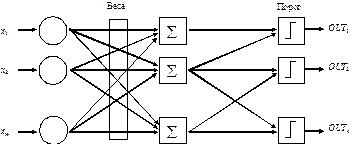 Рис. 13.6. Персептрон со многими выходами
Рис. 13.6. Персептрон со многими выходами
|
Нейроны второго слоя отмечают свойства или средства некоторого примера или изображения. Третий слой является выходным, и каждый нейрон в нем выдает или не выдает сигнал. Этот слой имеет обратную связь со вторым слоем. В начале работы персептрон не имеет полной связи между вторым и третьим слоями. Она будет создаваться в процессе обучения персептрона. Нейроны второго и третьего слоя вычисляют их вход, используя уравнение (13.8):
| NETi=SwjiOUTj+w0IOUT0 , | (13.8) |
где OUTj - выходы из нейронов предыдущего слоя. Нейроны третьего слоя имеют влияние фактора OUT с фиксированным значением w0i=1. Вес фактора w0i изменяется в процессе обучения. В этом контексте фактор OUT можно представить как выход нейрона второго слоя, равный 1.
Нейроны второго и третьего слоя используют передаточную функцию сигнум, рассмотренную в 13.1:
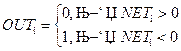
| (13.9) |
Из уравнения (13.9) видно, что данные NET и OUT дискретные и двоичные, т.е. 0 или 1.
Обучение персептрона. Процесс обучения заключается в формировании весов связей между вторым и третьим слоями в соответствии со следующим уравнением:
| wjiнов=wjiстар+a(DESOUTi-OUTi) | (13.10) |
где wji - весовая связь нейрона j второго слоя с нейроном i третьего слоя, DESOUTi - “желаемый” или правильный выход нейрона i третьего слоя и OUTi - реальный выход нейрона i.
Уравнение обучения персептрона имеет простое объяснение. Если нейрон i посылает правильный импульс (выход) во внешнюю среду, тогда веса к нейронам второго слоя не изменяются. Однако, если выход нейрона i равен единице, когда он должен быть равен нулю, тогда весовые связи с нейронами второго слоя уменьшаются путем умножения на величину a. Если с другой стороны, нейрон i имеет выход 0, когда правильный импульс равен 1, то весовые связи к нейронам второго слоя увеличиваются путем умножения на величину a, где 0£a£1. Значение должно быть положительным меньшим или равным единице.
Обучение персептрона происходит следующим образом. На вход персептрона подают множество образов по одному и подстраивают веса до тех пор, пока не будет, достигнут требуемый выход. Допустим, что образ (символ) изображен на странице в клетку и от каждой клетки на персептрон подается вход. Если в клетке имеется линия (часть изображения), то от нее подается 1, в противном случае - 0. Множество клеток задаёт, таким образом, множество нулей и единиц, которое подается на вход персептрона. Цель состоит в том, чтобы научить персептрон включать индикатор при подаче на него множества входов, задающих нечетное число, и не включать в случае четного.
Допустим, что вектор X(x1,...,xn) является образом нашего изображения, где компоненты xi(i=1,...n) соответствуют клеткам страницы. Каждая компонента вектора X умножается на соответствующую компоненту вектора весов W(w1,...,wn) и эти произведения суммируются, т.е.
Y=Sxiwi или в векторной форме Y = XW.
Если сумма превысит порог T, то выход нейрона равен единице (индикатор зажигается), в противном случае он равен нулю.
Обучение персептрона состоит в том, что на его вход подается образ X и вычисляется выход Y. Если Y является правильным, то веса не меняются. Однако, если выход неправилен, то веса изменяются так, чтобы уменьшить ошибочный результат.
Это объяснение можно представить в виде следующего алгоритма обучения:
1. Подать образ X на вход пересптрона и вычислить выход Y.
2. а) Если выход Y правильный, то перейти к шагу 1;
б) Если выход Y неправильный и равен 0, то добавить все входы к соответствующим им весам;
в) Если выход Y неправильный и равен 1, то вычесть вход из соответствующего ему веса.
3. Перейти к шагу 1.
За конечное число шагов сеть научится разделять страницы с изображениями, соответствующими четным и нечетным числам при условии, что множество чисел линейно разделимо. Это значит, что для всех страниц с нечетными числами выход будет больше порога, а для всех страниц с четными - меньше.
Дельта-правило. Имеется несколько важных вопросов, связанных с обучением персептрона, а именно, какое количество страниц с изображениями требуется подать на вход персептрона, чтобы его обучить, и в какой последовательности это сделать с тем, чтобы минимизировать процесс обучения.
Дельта-правило является обобщением алгоритма обучения и позволяет использовать непрерывные входы и выходы. Суть его состоит в следующем. Вводится величина, которая равна разности между требуемым или целевым выходом DESOUT и реальным выходом OUT:
| d=(DESOUT-OUT) | (13.11) |
Тогда шаг 2а соответствует случаю, когда d=0; шаг 2б - d>0, а шаг 2в - d<0.
В любом из этих случаев персептронный алгоритм обучения персептрона сохраняется, если d умножается на величину каждого входа xi и это произведение добавляется к соответствующему весу. С целью обобщения вводится коэффициент скорости обучения h, который умножается на d×xi, что позволяет управлять средней величиной изменения весов. То есть:
| Di=hdxi; | (13.12) |
| wi(n+1)=wi(n)+Di , | (13.13) |
где di - коррекция, связанная с i-м входом xi, wi(n) и wi(n+1) - значения весов соответственно до и после коррекции.
Дельта-правило изменяет веса в соответствии с требуемым и реальным значениями выхода каждой полярности, как для непрерывных, так и для бинарных входов и выходов.
Дата добавления: 2016-10-26; просмотров: 7738;











