ПРАКТИЧЕСКАЯ РАБОТА. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ

Цель. Рассмотреть на практических примерах использование теорем о свойствах делимости, уметь находить разными способами наибольший общий делитель и наименьшее общее кратное нескольких чисел.

Теоретическая часть

Вопросы к изучению

1. Отношение делимости и его свойства.

Признаки делимости.

Наименьшее общее кратное и наибольший общий делитель.

4. Простые числа.

5. Способы нахождения наибольшего общего делителя и наименьшего общего кратного чисел.

Основные понятия темы

Ø делитель данного числа;

Ø простое число;

Ø составное число;

Ø общий делитель данных чисел;

Ø наибольший общий делитель данных чисел;

Ø взаимно простые числа;

Ø общее кратное данных чисел;

Ø наименьшее общее кратное данных чисел.

Рассмотрены

Ø теоремы о свойствах де­лимости и признаках делимости на 2, 3, 4, 5, 9.

Ø дан способ получения признаков делимости на те составные числа, которые мож­но представить в виде произведения взаимно простых чисел.

Ø основная теорема арифметики, в которой утверждается, что любое составное число можно представить в виде произведе­ния простых множителей.

Правила

Ø нахождения наибольшего общего делителя двух чисел двумя способами. Первый основан на разложении данных чисел на простые множители, а второй является алгоритмом Евклида.

Ø Наименьшее общее кратное двух чисел можно находить, используя разложение данных чисел на простые множители, или, если известен наибольший общий делитель чисел а и b, то по формуле К(а,b) =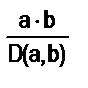

Практическая часть

Обязательные задания

1. Объясните, почему число 15 является делителем числа 60 и не яв­ляется делителем числа 70.

2. Постройте граф отношения «быть делителем данного числа», заданного на множестве Х = {2, 6, 12, 18, 24}. Как отражены на этом графе свойства данного отношения?

3. Известно, что число 24 - делитель числа 96, а число 96 – делитель числа 672. Докажите, что число 24 делитель числа 672, не выполняя деления.

4. Запишите множество делителей числа: а) 24; б)13; в)1.

5. На множестве Х = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} задано отношение «иметь одно и то же число делителей». Является ли оно отношением эквивалентности?

6. Докажите или опровергните следующие утверждения:

а) Если сумма двух слагаемых делится на некоторое число, то и каждое слагаемое делится на это число.

б) Если одно из слагаемых суммы не делится на некоторое число, то и сумма не делится на это число.

в) Если ни одно слагаемое не делится на некоторое число, то и сумма не делится на это число.

г) Если одно из слагаемых суммы делится на некоторое число, а другое не делится на это число, то и сумма не делится на это число.

7. Верно ли, что: а) аM m и bM n Þ а bM mn; б) аbM n Þ аM n или bM n.

8. Выпишите из ряда чисел 132, 1050, 1114, 364, 12000 те, которые: а) делятся на 2; б) делятся на 4; в) делятся на 2 и не делятся на 4; г) делятся и на 2 и на 4.

10. Верно ли утверждение:

а) Для того чтобы число делилось на 2, необходимо и достаточно, чтобы оно делилось на 4?

б) Для того чтобы число делилось на 2, достаточно, чтобы оно делилось на 4?

11. Из ряда чисел 72,312,522,483, 1197 выпишите те, которые: а) делятся на 3; б) делятся на 9; в) делятся на 3 и не делятся на 9;

г) делятся и на 3 и на 9. Сделайте вывод о взаимосвязи делимости на 3 и на 9. Докажите его.

12. Не выполняя сложения, установите, делится ли значение выраже­ния на 4:

а) 284+ 1440 + 113; в)284+ 1441 + 113;

б) 284 + 1440 + 792224; г)284 + 1441 + 113 + 164.

13. Не выполняя вычитания, установите, делится ли разность на 9.

а) 360 - 144; б) 946 - 540; в) 30 240 - 97.

14. Верно ли, что для делимости числа х на 8 в десятичной системе счисления необходимо и достаточно, чтобы на 8 делилось трехзначное число, образованное последними тремя цифрами десятичной записи числа х?

15. Даны числа 36 и 45.

а) Найдите все общие делители этих чисел.

б) Можно ли назвать все их общие кратные?

в) Найдите три трехзначных числа, которые являются общими кратными данных чисел.

г) Чему равны D(36, 45) и K(36, 45)? Как проверить правильность полученных ответов?

16. Верны ли записи: а) D(32, 8) =8 и K(32, 8) = 32; б)D (17,35)=1 и K(17,35)=595; в) D(255, 306) = 17 и K(255, 306) = 78030.

17. Найдите K(а,b), если известно, что:

а) а = 47, b = 105 и D(47, 105) = 1; б) a = 315, b = 385 и D (315, 385) =35.

18. Из множества чисел 1032, 2964, 5604, 8910, 7008 выпишите те, которые делятся на 12.

19. Делятся ли на 18 числа 1548 и 942?

20. К числу 15 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 15.

21. Найдите цифры а и b числа 72а-3 b, если известно, что это число делится на 45.

22. Не выполняя умножения и деления уголком, установите, какие из следующих произведений делятся на 30: а)105×20; б)47×12×5; в)85×33×7.

23. Не выполняя сложения или вычитания, установите, значения каких выражений делятся на 36. а) 72+180+252; б) 612-432; в) 180+252+100; г)180+250+200.

24. Из множества чисел 13, 27, 29; 51, 67 выпишите простые числа, а составные разложите на простые множители.

25. Докажите, что число 819 не является простым числом.

26. Разложите на простые множители числа 124, 588, 2700, 3780.

27. Какое число имеет разложение: а)2³ × 3²× 7× 13; б)2²× 3× 5³?

28. Найдите наибольший общий делитель и наименьшее общее кратное данных чисел, представив их в каноническом виде: а) 948 и 624; б)120,540,418.

Творческие задания

1. Докажите, что при любом натуральном n истинны утверждения:

а) n(n+ 1)(n+2) M 6; б) n(n+1)(n+2)(n+3) M 12.

2. Сформулируйте признаки делимости на 12,15,18,36,45,75.

3. Используя алгоритм Евклида, найдите наибольший общий делитель чисел. а) 846 и 246; б) 585 и 1960; в) 15283 и 10013.

4. Верно ли, что: а) D(448, 656) = 16; б) K(578, 8670) = 8670?

5. Докажите, что числа 432 и 385 взаимно простые.

6. Найдите наибольший общий делитель всех пятизначных чисел, записанных при помощи цифр 1, 2, 3, 4, 5 (цифры в записи чисел не повторяются).

7. Узнать, какой день недели будет 1 января 2020 г. (при условии, что действующий календарь сохранится).

8. Найти остаток от деления на 3 числа А= -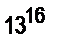

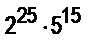
9. Доказать утверждения: 1) 0:а; 2) а:1; 3) если 1:а, то а=1.