Сложение положительных рациональных чисел коммутативно и ассоциативно,

("а, b Î Q₊) а + b= b + а;

("а, b, с Î Q₊) (а + b)+ с = а + (b+ с)

Прежде чем сформулировать определение умножения положительных рациональных чисел, рассмотрим следующую задачу: известно, что длина отрезка Х выражается дробью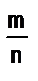 при единице длины Е, а длина единичного отрезка измерена при помощи единицы Е₁ и выражается дробью . Как найти число, которым будет представлена длина отрезка X, если измерить ее при помощи единицы длины Е₁?

Так как Х=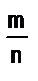Е, то nХ=mЕ, а из того, что Е = 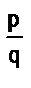Е₁ следует, что qЕ=рЕ₁. Умножим первое полученное равенство на q, а второе – на m. Тогда (nq)Х = (mq)Е и (mq )Е= (mр)Е₁, откуда (nq)X= (mр)Е_1. Это равенство показывает, что длина отрезка х при единице длины выражается дробью 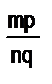, азначит, 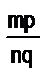= 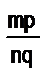, т.е. умножение дробей связано с переходом от одной единицы длины к другой при измерении длины одного и того же отрезка.

Определение.Если положительное число а представлено дробью , а положительное рациональное число b дробью 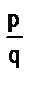, то их произведением называется число а b , которое представляется дробью .

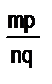Умножение положительных рациональных чисел коммутативно, ассоциативно и дистрибутивно относительно сложения и вычитания.Доказательство этих свойств основываетсяна определении умножения и сложения положительных рациональных чисел, а также на соответствующих свойствах сложения и умножения натуральных чисел.

Определение сложения положительных рациональных чисел дает возможность определить отношение «меньше» на множествеQ₊.

Определение. Пусть а иb - положительные рациональные числа. Считают, что число b меньше числа а, если существует такое положительное рациональное число с, что а = b + с.

В этом же случае считают, что число а больше числа b. Пишут b < а, а> b.

Так определенное отношение «меньше» обладает рядом свойств, которые мы приводим без доказательства.

1. Отношение «меньше» на множестве Q₊ антисимметрично и транзитивно, т.е. является отношением порядка, а множество Q₊ упорядоченным множеством.

2. Если рациональные числа а и b представлены дробям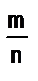и и 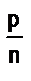(т.е. дробями, имеющими одинаковые знаменатели), то а < b в том и только в том случае, когда m < р.

3. Если рациональные числа а и b представлены дробям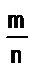ии 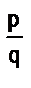(т.е. дробями, имеющими разные знаменатели), то а < b в том и только в том случае, когда т q < nр.

4. В множестве положительных рациональных чисел нет наименьшего числа.

5. Между любыми двумя различными числами а и b из Q₊ заключено бесконечно много чисел этого же множества. Это свойство называют свойством плотности множества Q₊.

6. В множестве положительных рациональных чисел нет наибольшего числа.

Вычитание положительных рациональных чисел определяется как операция, обратная сложению, т.е. это такая операция, которая удовлетворяет условию: а - b = с тогда и только тогда, когда а = b + с.

Разность а - b положительных рациональных чисел существует тогда и только тогда, когда b < а. Если разность а - b существует, то она единственна.

Используя определение и условие существования разности, можно получить правило вычитания положительных рациональных чисел,представленных дробям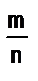и и 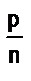, где т < р : /

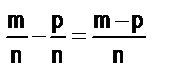Деление положительных рациональных чисел определяется как операция, обратная умножению, т.е. это такая операция, которая удовлетворяет условию: а:b=с тогда и только тогда, когда а = bс.

Из этого определения и правила нахождения произведения положительных рациональных чисел можно получить правило деления положительных рациональных чисел, представленных дробям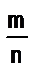ии : .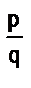

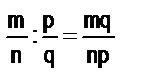Из этого правила следует, что частное положительных рациональных чисел всегда существует.

<72 73 747576 77 78 >

Дата добавления: 2021-01-26; просмотров: 333;