Понятие о плоско-параллельном движении твердого тела

Примером плоско-параллельного движения могут служить движение шатуна кривошипно-шатунного механизма, движение колеса нa прямолинейном участке пути и др.

Покажем, что любое перемещение плоской фигуры можно осуществить двумя простейшими движениями: одним поступательным и одним вращательным. Положение плоской фигуры на рис. 31, а вполне определяется отрезком А₁В₁. Этот отрезок можно переместить изположения І в положение ІІ - следующим образом: перенести его параллельно самому себе в положе­ние А₂ 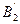, (при этом фигура совершит поступательное перемещение), а затем повернуть отрезок вокруг точки А₂ против часовой стрелки на угол φ, (фигура при этом совершит вращательное движение и займет положение ІІ). Можно поступить иначе: вначале дать фигуре поступательное перемещение до положения отрезка В₂ 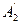, а затем повернуть вокруг точки В₂ против часовой стрелки опять на угол φ.

Точку, вокруг которой фигура совершает поворот, называют полюсом. В первом случае полюсом была точка А ₂, во втором — В₂. Очевидно, за полюс может быть принята произвольная точка фигуры.

Итак, плоско-параллельное движение можно разло­жить на два составляющих движения: поступательное вместе с некоторым полюсом и вращательное вокруг этого полюса. Поступательная часть плоско-параллельного дви­жения зависит от выбора полюса. Как видно из рис. 31, а, поступательное перемещение А₁А₂ при выборе за полюс точки А ₂ не равно поступательному перемещению B₁B₂ при выборе за полюс точки В₂.

Рассматривая вращательную часть плоско-параллель­ного движения, нетрудно установить, что угол поворота не зависит от выбора полюса.

Разложение плоско-параллельного движения можно использовать для определения скоростей точек тела. Так как плоско-параллельное движение фигуры может быть представлено как сумма двух движений — посту­пательного и вращательного, то скорость любой точки тела В (рис. 31, б) можно представить как геометриче­скую сумму двух скоростей: скорости 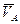движения по­люса А и скорости 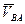вращательного движения точки В вокруг полюса А:

= + .

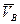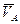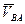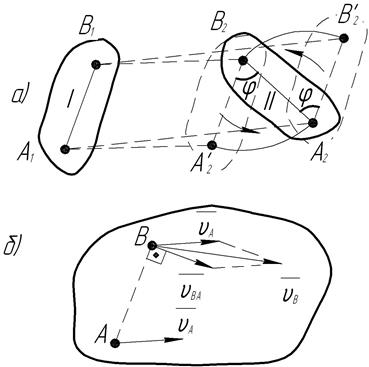
Рис. 31. Плоско-параллельное движение твердого тела.

Величина скорости вращательного движения опреде­лится по формуле

V_BA = ω AB,

где ω — угловая скорость вращения точки В относительно точки А;

АВ — радиус вращения точки В относительно по­люса А.

Скорость вращательного движения 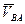направлена перпендикулярно радиусу вращения АВ.

Так как вращательная часть движения не зависит от выбора полюса, то общая для всех полюсов угловая скорость ω называется угловой скоростью плоской фигуры.

Рассуждая аналогично, можно показать , что ускорение точки В запишется как

= + + ,

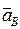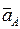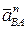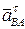где а_А – ускорение точки А как полюса;

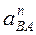- нормальное ускорение вращения точки В вокруг точки А;

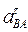- тангенциальное ускорение вращения точки В вокруг точки А.

Вектор 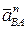направлен параллельно отрезку АВ в сторону полюса – точку А. Его величина определится по формуле

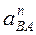= ω²АВ

Вектор 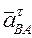перпендикулярен отрезку АВ инаправлен в сторону углового ускорения ε вращения телавокруг полюса.Его величина определится как

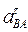= εАВ.

3.4. Аксиомы динамики.

В динамике рассматривается движение материальных точек или тел под действием приложенных сил; устанав­ливается связь между приложенными силами и вызывае­мым ими движением.

Динамика изучает такие системы сил, которые не находятся в состоянии равновесия. Она основывается на ряде вытекающих из опыта аксиом; некоторые из них были рассмотрены ранее в статике.

Напомним содержание первой аксиомы, так называе­мого закона инерции, рассмотренного в статике .

Система сил, приложенная к материальной точке, является уравновешенной, если под ее воздействием точка находится в состоянии относительного покоя или движется равномерно и прямолинейно. Таким образом, первая аксио­ма определяет условия, при которых система сил взаимно уравновешена и, следовательно, эквивалентна нулю.

Однако аксиома имеет еще и другой смысл, на котором следует остановиться подробнее. В случае относительного покоя или равномерного и прямолинейного движения уско­рение материальной точки равно нулю. Поэтому под дей­ствием уравновешенной системы сил или при отсутствии силовых воздействий материальная точка не испытывает ускорений и движется равномерно и прямолинейно.

Когда на точку действует неуравновешенная система сил, точка будет иметь некоторое ускорение. Связь ме­жду действующей на точку силой и ускорением, вызы­ваемым этой силой, устанавливается второй аксиомой ди­намики, которая заключается в следующем:

Ускорение 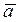, сообщаемое материальной точке прило­женной к ней силой 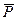, имеет направление силы и по величине пропорционально ей (рис. 32, а):

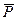= т ,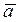

где m — коэффициент пропорциональности, связыва­ющий силу с ускорением, появившимся в ре­зультате приложения силы.

Уравнение называется основным уравнением ди­намики в векторной форме. Оно справедливо также и в скалярной форме

Р = та.

Различие между первой и второй формами заключается в том, что векторная форма уравнения учитывает направ­ление векторов силы и ускорения, а скалярная форма учитывает только численные значения этих величин.

Коэффициент т, входящий в основное уравнение ди­намики, имеет очень важное физическое значение. Он представляет собой массу материальной точки.

Если решить уравнение относительно уско­рения, получим

а = .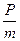

Из этого уравнения видно, что чем больше масса, тем большая сила потребуется для сообщения телу определен­ного ускорения. Следовательно, масса ха­рактеризует «инертность», или «неподатливость» тела воздействию силы.

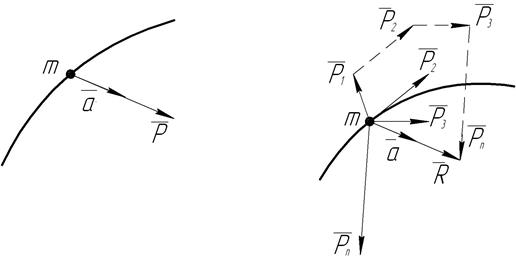
Рис. 32. Векторы силы и ускорения.

Таким образом, масса материальной точки является мерой ее «инертности».

Для вращательного движения тела основное уравнение динамики имеет вид

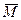= I ,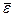

где I – момент инерции тела (мера инертности тела во вращательном движении); ε - угловое ускорение.

Приведем формулировку аксиомы независимости дей­ствия сил.

Если на материальную точку действует несколько сил, то ускорение, получаемое точкой, будет таким же, как при действии одной силы, равной геометрической сумме этих сил (рис. 32, б), т. е.

т = + + + . . .+ = ,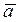

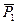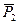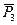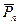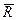где 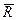- равнодей­ствующая системы сил, приложенных к рассматриваемой точке.

Остановимся на последней аксиоме динамики — ак­сиоме взаимодействия, знакомой из статики.

Всякому действию соответствует равное и противо­положно направленное противодействие. Иными словами, силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю и направлены по прямой, соединяющей эти точки, в противоположные стороны.

3.5. Понятие о силах инерции. Метод кинетостатики

Рассмотрим материальную точку А, на которую дей­ствует некоторая система сил 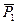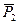, , 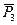. . ., 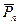(рис. 33). Среди действующих сил могут быть заданные активные силы, а также реакции связей.

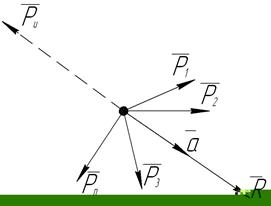
Рис.33. Сила инерции.

На основании аксиомы независимости действия сил точка А под действием этих сил получит такое же ускорение, как если бы на нее действовала лишь одна сила, равная геометриче­ской сумме заданных сил

т = + + + . . .+ = ,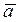

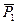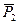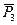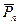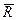Предположим, что кроме сил 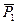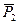, , 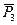. . ., 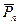на точку действует еще одна сила 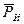, по величине равная равнодействующей силе 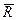и направленная в сторону, противоположную равнодействующей силе (рис.33)

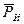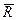= - = - т = -( + + + . . .+ ).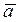

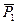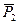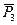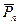Это уравнение можно представить в виде

(- т 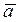) + + 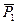+ + 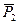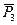. . .+ 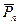= 0.

или

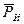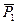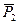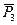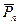+ + + + . . .+ = 0.

Таким образом, все силы, включая силу 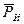, должны уравновешиваться, так как силы 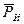и 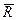равны между собой и направлены по одной прямой в противоположные стороны. Сила 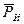, равная произведению массы точки на ее ускорение, но направленная в сторону, противополож­ную ускорению, называется силой инерции.

Итак, из последнего уравнения следует, что в каждый данный момент времени силы, приложенные к материаль­ной точке, уравновешиваются силами инерции. Приве­денный вывод называют началом или прин­ципом Даламбера; он может быть применен не только к материальной точке, но и к твер­дому телу или к системе тел. В последнем случае он фор­мулируется следующим образом: если ко всем реально действующим силам, приложенным к движущемуся телу или системе тел, приложить силы инерции, то получен­ную систему сил можно рассматривать как находящуюся в равновесии.

Следует подчеркнуть, что силы инерции действительно существуют, но приложены не к движущемуся телу, а к тем телам, которые вызывают движение, т. е. к связям.

Применение принципа Даламбера позволяет свести решение динамических задач к использованию уравнений равновесия, т. е. к замене задачи динамики эквивалент­ной ей задачей статики. Такой прием решения задач динамики носит название метода кинетостатики.

ГЛАВА 4. ОСНОВЫ ТЕОРИИ МЕХАНИЗМОВ И МАШИН.