Скорости и ускорения точек вращающегося тела.

Точки тела, вращающегося вокруг оси, перемещаются по окружностям (рис. 30, а), радиусы которых r равны расстояниям точек от оси вращения.

Линейная скорость V точки А и угловая скорость ω тела cвязаны между собою линейной зависимостью

V_А= ω r.

Подставив в формулу для линейной скорости точек тела, вращающегося вокруг неподвижной оси, значение n угловой скорости в оборотах в минуту, получим

V_А= 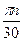r.

Направлена 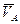по перпендикуляру к радиусу r в сторону ω (рис.30, а).

В общем случае вектор скорости точки А, вращаясь вокруг точки О, изменяется по величине и направлению. Поэтому у этой точки будет иметь место нормальное ускорение 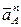(характеризует изменение 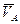по направлению) и тангенциальное ускорение 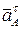(характеризует изменение 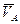по величине). Величина нормального ускорения 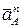точки А определится как

= .

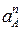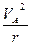Подставляя в это выражение значение скорости V_А= ω r, получаем

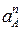= ω² r.

Направлено 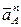по радиусу r к центру О вращения.

Касательное ускорение точки определяется из выражения

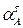=ε r,

где ε – угловое ускорение вращающегося тела.

Направлено 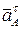перпендикулярно r в сторону ε.

Полное ускорение точки при неравномерном вращении вокруг оси (рис. 30, б) геометрически складывается из касательного и нормального ускорений

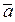_А = + .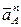

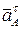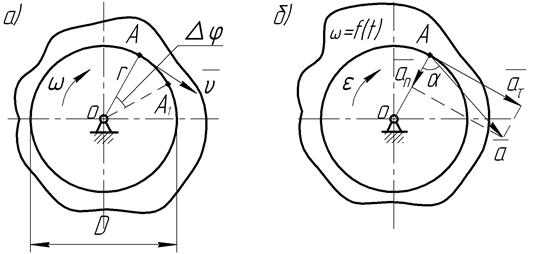
Рис. 30. Скорости и ускорения точки вращающегося тела.