Определение современной стоимости р-срочной ренты с начислением процентов m в раз в год
Предположим, что начисление процентов производится m раз в год в течение n лет по номинальной ставке i. Каждый раз проценты начисляются по ставке 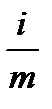 . Количество начислений – mn. В общем случае современная стоимость финансовой ренты может быть определена по формуле
. Количество начислений – mn. В общем случае современная стоимость финансовой ренты может быть определена по формуле
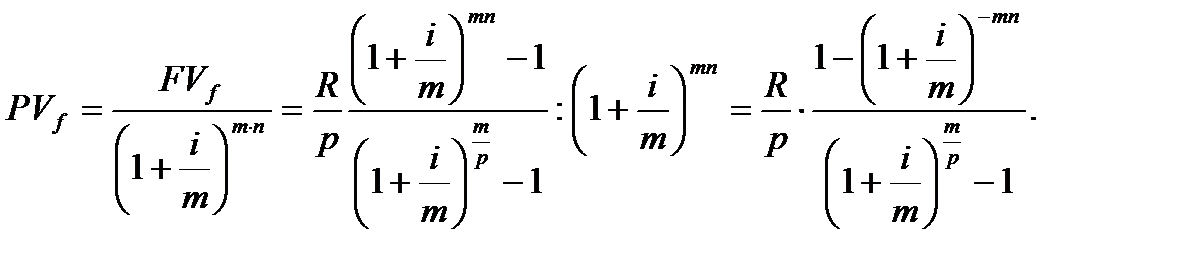 (6.9)
(6.9)
Пример. Ежеквартально в течение 2 лет на специальный счет поступает 100 тыс. у.е. Определить современную стоимость финансовой ренты, если проценты по ставке 12% годовых начисляются ежемесячно.
Решение: 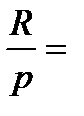 100 тыс. у.е.; p = 4; i = 0,12;n = 2; m=12.
100 тыс. у.е.; p = 4; i = 0,12;n = 2; m=12.
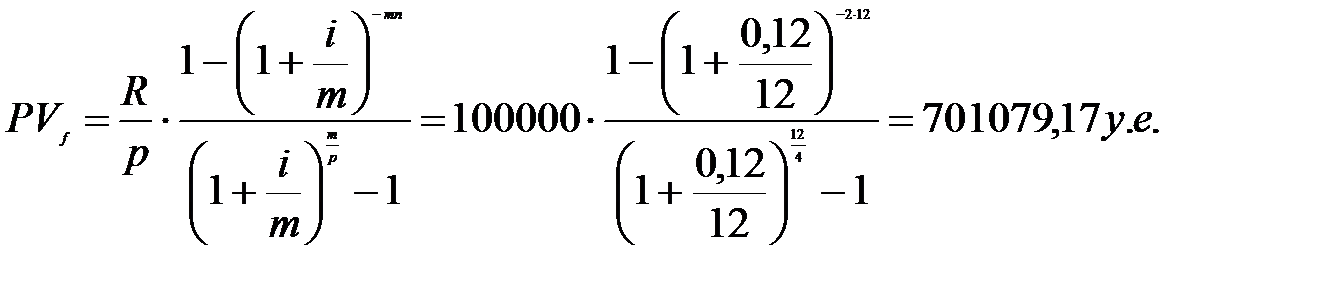
Следовательно, современная стоимость данной финансовой ренты 701 079 у.е.
Вечные ренты
Наращенная сумма вечной ренты при любых ее параметрах равна бесконечно большой величине, в то же время ее современная величина имеет конкретное значение.
Современная величина вечной ренты оказывается полезной характеристикой в ряде финансовых расчетов, например при замене некоторых потоков платежей, оценке финансовых инвестиций, в страховых расчетах.
Современная величина вечной годовой ренты определяется по формуле:
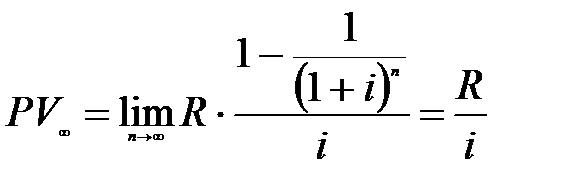 (6.10)
(6.10)
Пример. Квартира арендована за 10000 у.е в год. Какова выкупная цена аренды при годовой ставке процента 5%?
Решение: R = 10 000 $; i = 0,05. Выкупная цена ренты – это современная величина всех будущих арендных платежей. Она равна 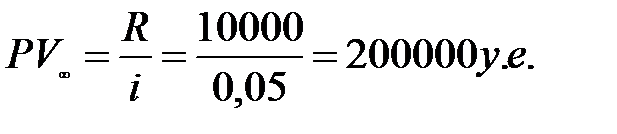 .
.
Заметим, что если поместить 200000 у.е в банк под 5% годовую ставку, то годовые процентные деньги составят в точности 10 000 у.е.
Формула для вычисления современной стоимости р-срочной вечной ренты с начислением процентов m раз в году имеет вид:
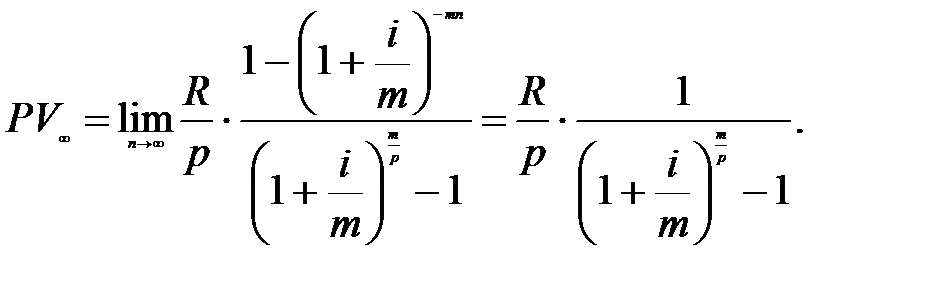 (6.11)
(6.11)
Пример. Определите цену вечной ренты, выплаты по которой в конце каждого месяца составляют 2 тыс. у.е. при номинальной процентной ставке 12% годовых и ежеквартальном начислении процентов.
Решение: 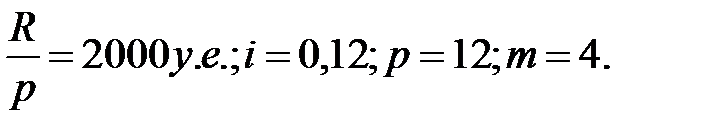
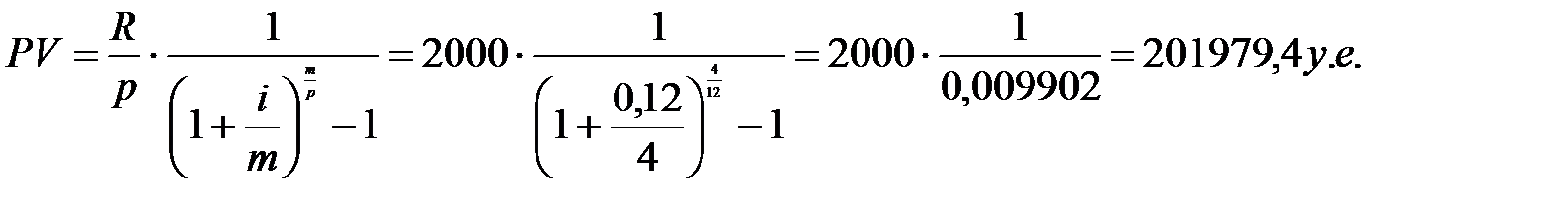
Конверсия рент
В ряде случаев возникает необходимость принять условия финансового соглашения, предусматривающего выплату ренты.
Определение: Процесс, связанный с изменением условий ренты, называется конверсией ренты.
Иногда конверсия ренты заключается в замене ренты единовременным платежом. Иногда рента с одним набором условий заменяется рентой с другими условиями. При этом предполагается, что конверсия рент не приводит к изменению финансовых последствий для каждого из участвующих в соглашении сторон, то есть она должна основываться на принципе финансовой эквивалентности платежей. При этом находят современную величину данной ренты, а затем подбирают ренту с такой же современной величиной и нужными параметрами.
Пример. Годовую ренту пренумерандо со сроком 5 лет, разовым платежом R=2000 у.е. и процентной ставкой i =6% необходимо заменить рентой сроком 8 лет. Определите параметры ренты.
Решение: R1=2 000 у.е.; i=0,06; n1=5;n2=8.
1).Определим современную стоимость такой ренты.
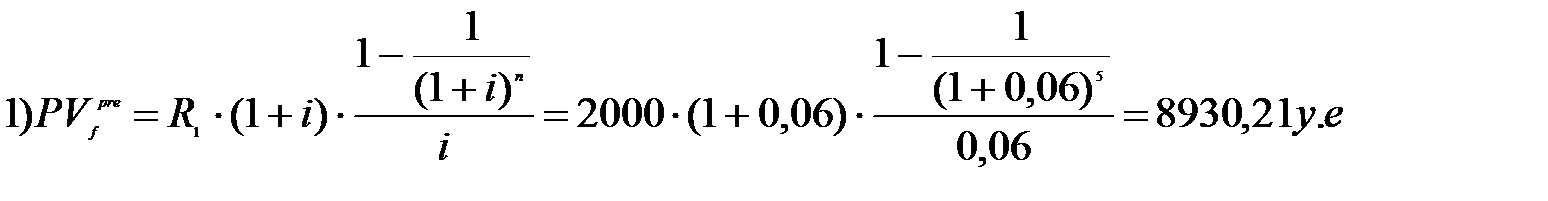
2). Найдем разовый платеж восьмилетней ренты с такой же современной стоимостью. Для этого составим уравнение эквивалентности:
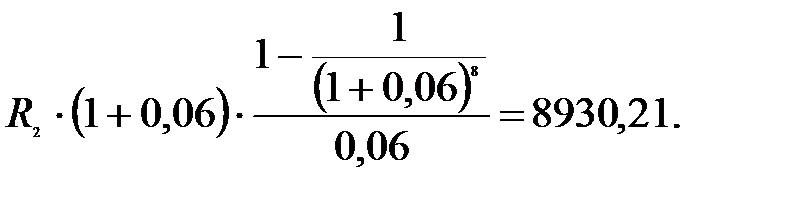
3). Разрешим это уравнение относительно 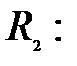
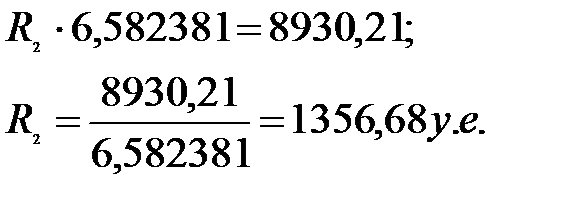
Объединение рент
Предположим, несколько рент необходимо заменить одной. Замена базируется на принципе финансовой эквивалентности обязательств, который реализуется путем составления уравнения эквивалентности.
При составлении уравнения эквивалентности находят современные величины рент-слагаемых и суммируют, а затем приравнивают эту сумму современной стоимости заменяющей ренты.
Правило объединения рент:
1) находят современные величины рент-слагаемых и суммируют их;
2) приравнивают полученную сумму современной стоимости заменяющей ренты;
3) задав все параметры заменяющей ренты, кроме одного, из уравнения эквивалентности определяют недостающий параметр.
Пример. Найти ренту-сумму для двух годовых рент постнумерандо: одна – длительностью 5 лет с годовым платежом 1000 у.е., а другая – 8 лет с годовым платежом 800 у.е. Годовая ставка процента равна 8%.
Решение: 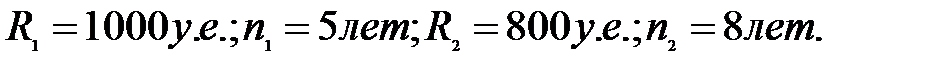
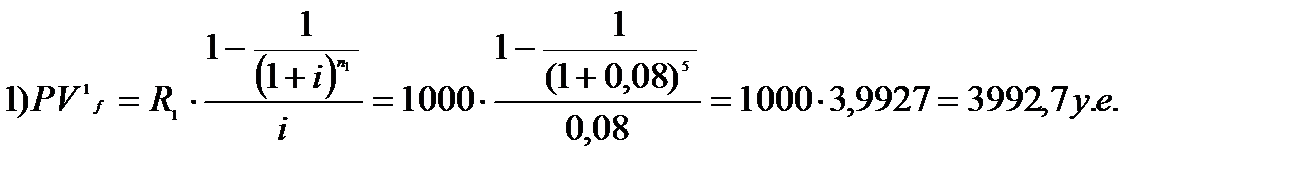 – современная величина первой ренты.
– современная величина первой ренты.
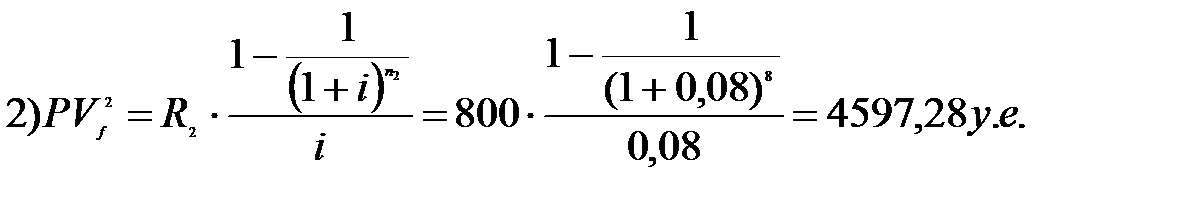 – современная величина второй ренты.
– современная величина второй ренты.
3) Определим современную величину ренты-суммы:3992,7+4597,28=8590,02=8589,98 у.е.
Теперь можно задать либо длительность ренты-суммы, либо годовой платеж и затем определить второй из этих параметров.
Предположим, что рента – сумма имеет длительность 6 лет, тогда уравнение эквивалентности имеет вид:
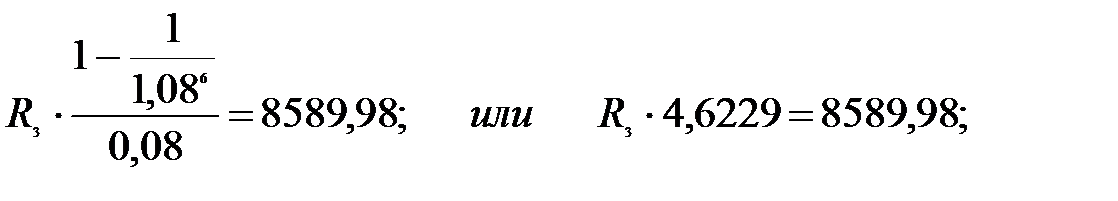
Отсюда: 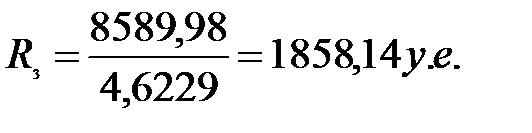 .
.
Дата добавления: 2019-09-30; просмотров: 698;











