Собственные колебания кузова на рессорах с линейными упругими элементами с гасителем колебаний вязкого трения.

До сих пор здесь рассматривалась консервативная система, в которой отсутствуют потери энергии колебаний. В действительности же при всех колебаниях системы в ней имеет место трение, при котором энергия колебаний превращается в тепло и рассеивается в окружающее пространство. Более того, в тех случаях, когда конструкторы заинтересованы в быстром уменьшении амплитуд колебания в системе, они в конструкциях, подверженных колебаниям, специально устанавливают гасители колебаний. В частности, в рессорном подвешивании вагонов всегда предусматривается гашение колебаний тем или иным путем, а чаще всего прямой постановкой специальных гасителей колебаний. Описание конструкций гасителей колебаний в рессорном подвешивании вагонов дано в курсе «Конструкции вагонов».

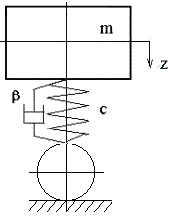Сначала рассмотрим свободные колебания системы с одной степенью свободы и гидравлическим гасителем колебаний (сила пропорциональна скорости).

Уравнение движения:

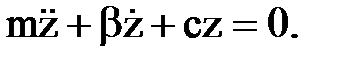(2.1)

Разрешим это уравнение относительно старшей производной и приведем к нормальной форме – к системе дифференциальных уравнений, каждое из которых первого порядка.

Для этого введем обозначения: z=q₁, 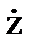=q₂.

В нормальной форме математическая модель имеет вид: 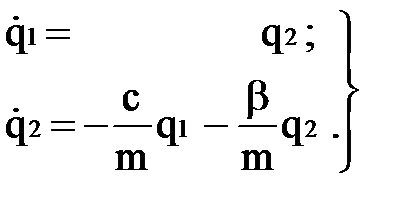(2.2)

Решение этой системы ищем в виде следующих функций: 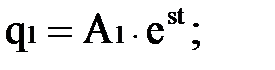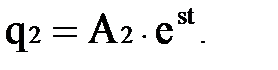(2.3)

Подставив функции (2.3) в систему (2.2), перенеся все члены влево и прировняв коэффициенты при 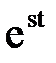к нулю, получим следующую систему однородных алгебраических уравнений:

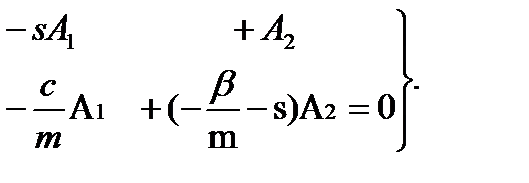(2.4)

Система (2.4) имеет ненулевое решение относительно неизвестных A₁ и A₂ только в случае равенства нулю её определителя:

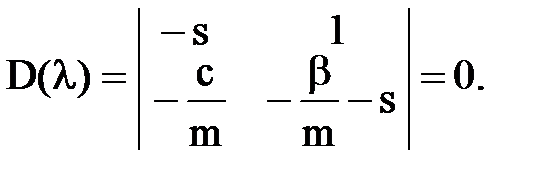(2.5)

Полученный определитель называется характеристическим. Раскрыв его получим характеристическое уравнение:

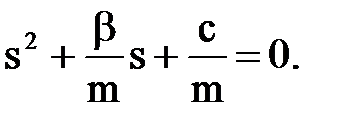
Если s равно одному из корней характеристического уравнения, то условие (2.5) будет выполнено. Корни этого уравнения при условии — 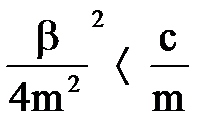являются комплексно-сопряженными числами и определяются выражениями — 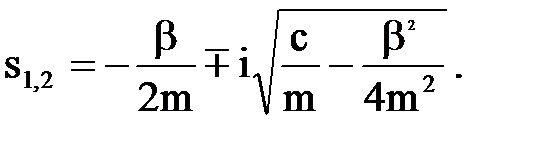(2.6)

Величина параметра β называется критической, если её определить из условия равенства нулю подкоренного выражения в (2.6),то есть

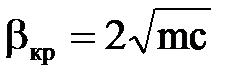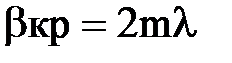или , где 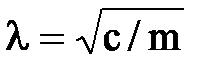– собственная частота одноосного вагона без трения в подвешивании.

Введем понятие коэффициента относительного демпфирования D как отношение параметра β к его критической величине: D=β/β_кр. Используя понятия и выражения, определяющие λ и D, выражения для корней характеристического уравнения приведем к виду

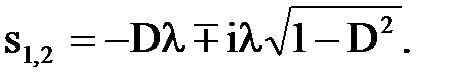(2.7)

Используя выражения (2.7), решение исходного уравнения (2.1) представим суммой частных решений, соответствующих s₁ и s₂:

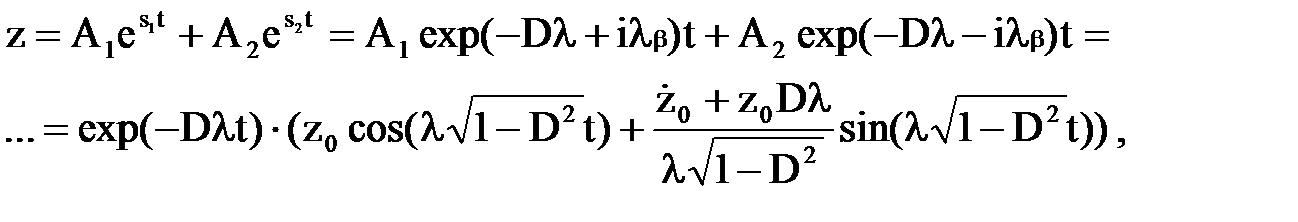
где 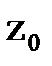, 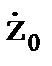– начальные условия (смещение и скорость смещения кузова при t=0).

Если принять начальную скорость равной нулю ( 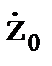=0), и сложить гармонические составляющие процесса, то решение примет вид

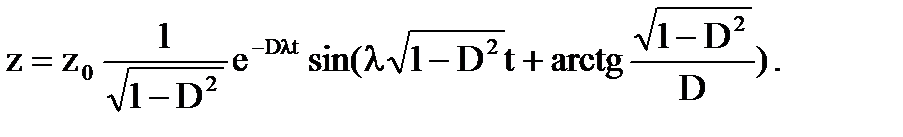
(2.8)

Введя обозначения:

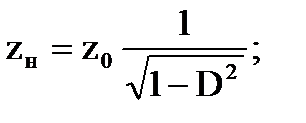
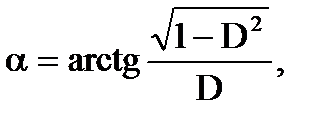
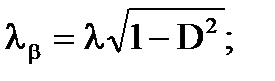
(2.9)

решение можно представить в более компактной форме

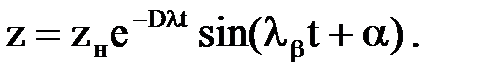(2.10)

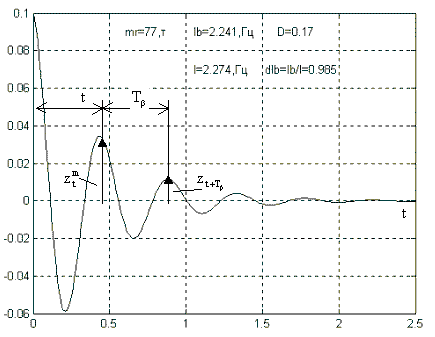
Графически процесс затухающих колебаний соответствующих решению (2.10) представлен на рис. 2.2.

Рис. 2.2. Процесс затухающих колебаний

Скорость затухания этого процесса оценивается следующими его характеристиками: коэффициентом затухания – ψ, равным отношению амплитудных отклонений процесса, сдвинутых по времени на один период и логарифмическим декрементом – δ. Выражения, определяющие эти характеристики можно представить в виде

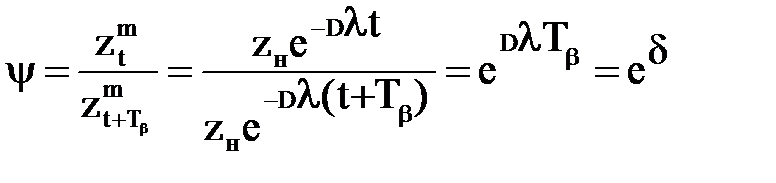, (2.11)

Из соотношений (2.11) следует, что амплитудные отклонения кузова в прцессе затухающих колебаний изменяются по закону геометрической прогрессии, то есть последующее отклонение равно произведению предыдущего на постоянное число – знаменатель прогрессии. Если рассматривать амплитудные отклонения в одном направлении от положения равновесия, то знаменателем прогрессии будет - 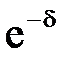, если в обоих – 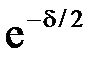. Соотношения между членами прогрессии в этих случаях будут представляться, соответственно:

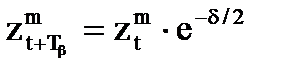
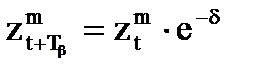
или (2.12)

Коэффициентом затухания можно пользоваться для оценки скорости затухания процесса, однако, более часто для этой цели пользуются логарифмическим декрементом – δ,

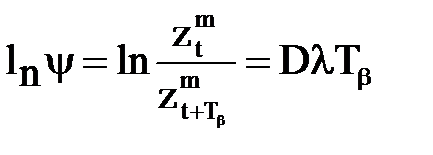=δ. (2.13)

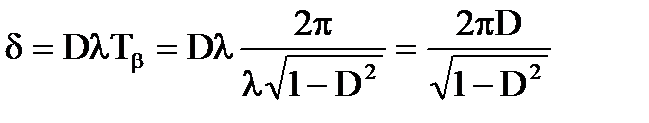Простейшие преобразования дают возможность получить следующие соотношения между δ и D:

. (2.14)

Разрешив выражение (2.14) относительно D будем иметь

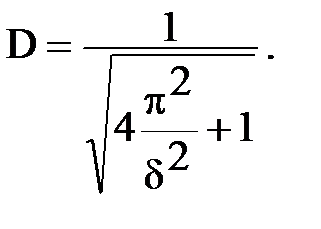(2.15)

Таким образом, "вязкое" трение существенно влияет на следующие динамические свойства вагона (свойства вагона как динамической системы):

Скорость затухания свободных колебаний;

Величину частоты свободных колебаний (собственной частоты).