Основные задачи теории колебаний
Колебания вагона на рессорном подвешивании
Общие сведения о факторах, способствующих возникновению колебаний вагонов. Характеристики колесных пар, обуславливающие колебательные движения. Путь и его характеристики, влияющие на динамические процессы вагонов.
Колебания вагонов, как известно, возникают потому, что колесные пары при своем движении по рельсам и стрелочным переводам совершают сложные пространственные перемещения и тем самым заставляют колебаться на рессорном подвешивании рамы тележек, раму кузова, кузов и сам путь. Таким образом, колебания вагона начинаются с колесной пары и передаются всем остальным деталям вагона и пути. Поэтому и следует рассмотреть вопрос о том, почему зарождаются колебания колеса.
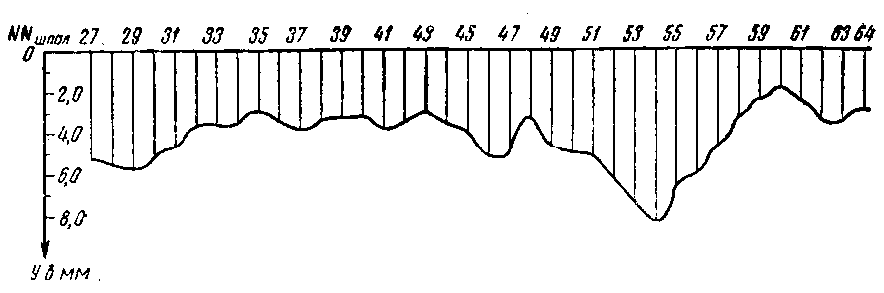
Рис. 1
Рассмотрим, прежде всего, вертикальные колебания одной колесной пары.
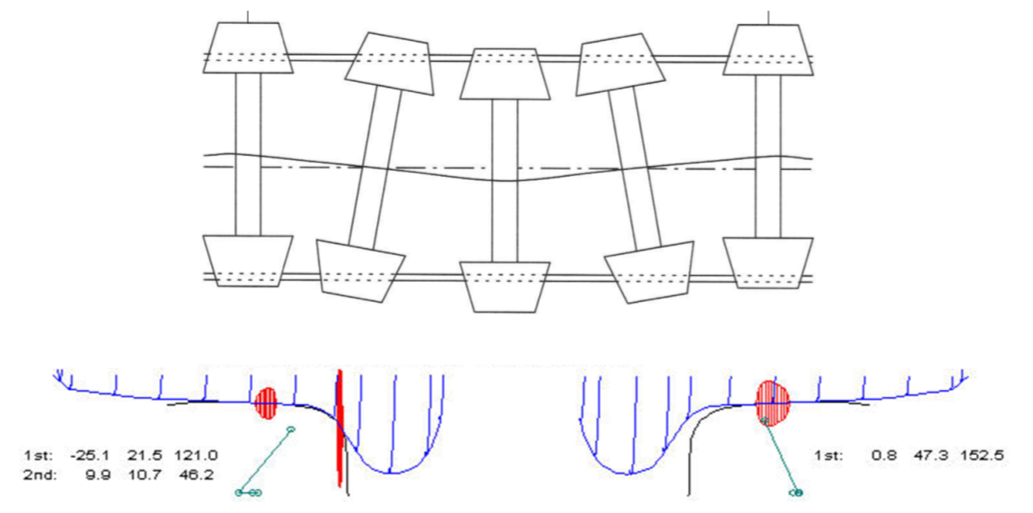
Фактическая траектория движения колеса определяется геометрическими формами рельса, в частности, его остаточным изгибом, неровностями на поверхности катания, зазорами между рельсами и шпалами, шпалами и балластом и т.п. Образец фактического продольного профиля пути, снятого весьма точной нивелировкой с определением высот точек на поверхности головки рельса приведен на рис. 1. Однако в системе таких неровностей всегда имеются, так называемые, «единичные» неровности, вызванные такими причинами, как одиночно просевшая шпала, крестовина на стрелочном переводе, пробоксовина (местный износ из-за боксования) на рельсе, зимой местное вспучивание пути (пучинa) и т. п. Кроме того, на пути имеются, так называемые «регулярные» неровности. К ним, прежде всего, относятся неровности, возникающие в рельсовых стыках.
При движении вагона по звеньевому пути, т.е. пути, состоящему из отдельных рельсов, соединенных в стыках накладками, всегда возникают соударения колес с рельсами.
Рассмотрим схематически этот процесс. Из-за того, что изгибная жесткость накладок, соединяющих концы рельсов, меньше изгибной жесткости рельса, прогиб пути в стыке под нагрузкой всегда больше прогиба в средней части рельсового звена. Поэтому, если колесо движется со скоростью v, то оно в последний момент движения по рельсу №1, не доходя до его конца, начинает вращаться вокруг точки А, как вокруг мгновенного центра вращения; при этом вектор скорости v1 направлен перпендикулярно линии АО (рис.2).
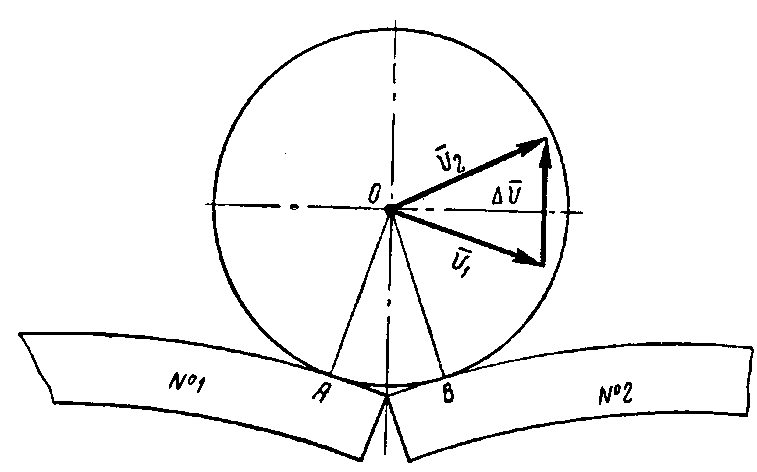
Рис. 2
В момент контакта колеса в точке В мгновенный центр вращения сразу же скачком (за время dt) перемещается в точку В и вектор скорости колеса v2 получает направление, перпендикулярное линии ОВ. Таким образом, колесо мгновенно изменяет скорость с v1 на v2, т.е. изменение скорости равно вектору
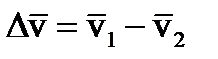 (1.1)
(1.1)
Если масса колеса равна т, то значит за какой-то отрезок времени dt количество движения колеса изменится на величину 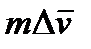 .
.
Из теоретической механики известно, что изменение количества движения тела за время dt равно импульсу сил, сообщенному телу за то же время, т. е.
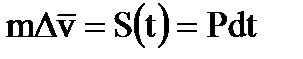 (1.2)
(1.2)
где S(t) — мгновенный ударный импульс;
Р — сила, возникающая при этом импульсе.
Таким образом, в стыке всегда возникает дополнительная динамическая сила Р, передаваемая и пути и вагону. Для вагона она является источником возникновения колебаний, а для пути — источником повышения просадок шпал в балласте.
В результате возникновения этих просадок продольный профиль пути приобретает вид, показанный на рис. 3.
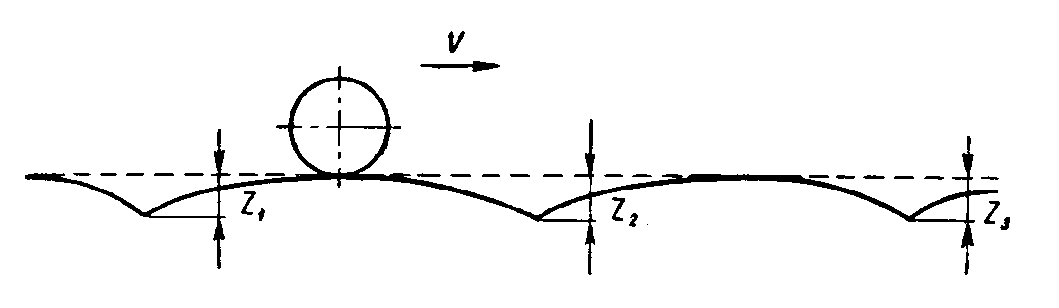
Рис. 3
Совершенно очевидно, что при таком продольном профиле пути колесо вынуждено неравномерно во времени перемещаться в пространстве, что приводит к силам инерции колеса, передаваемым через связи колеса с тележкой другим элементам вагона и пути. Естественно, что это также является одной из причин возникновения колебаний вагонов. К этому следует добавить, что ударные процессы возникают на каждом колесе одной колесной пары не одновременно из-за различного износа стыков, различия в их прогибах и сдвижке стыков друг относительно друга по длине пути.
Траектории движения колес одной колесной пары по просевшим стыкам различны потому, что остаточные просадки разных стыков не одинаковы. Поэтому наряду с вертикальными перемещениями каждого колеса колесная пара из-за различия в этих перемещениях совершает угловые перемещения (рис. 4). Соответствующая неровность рельсового пути носит название «перекос».
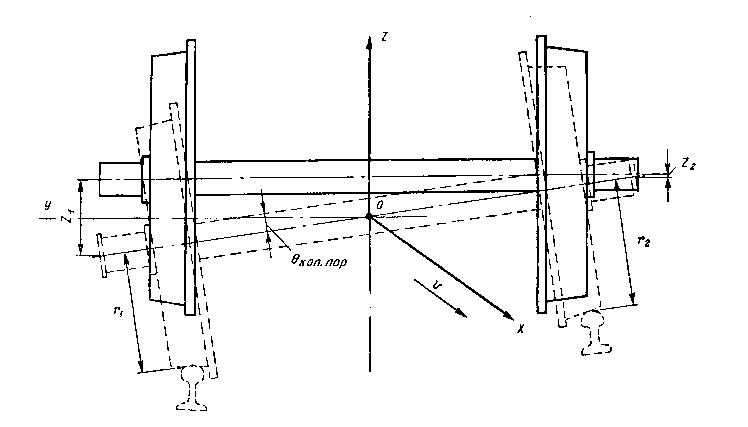
Рис. 4
Помимо вертикальных неровностей, рельсовый путь также характеризуется горизонтальными неровностями: уширением колеи и отклонением средней линии от оси пути.
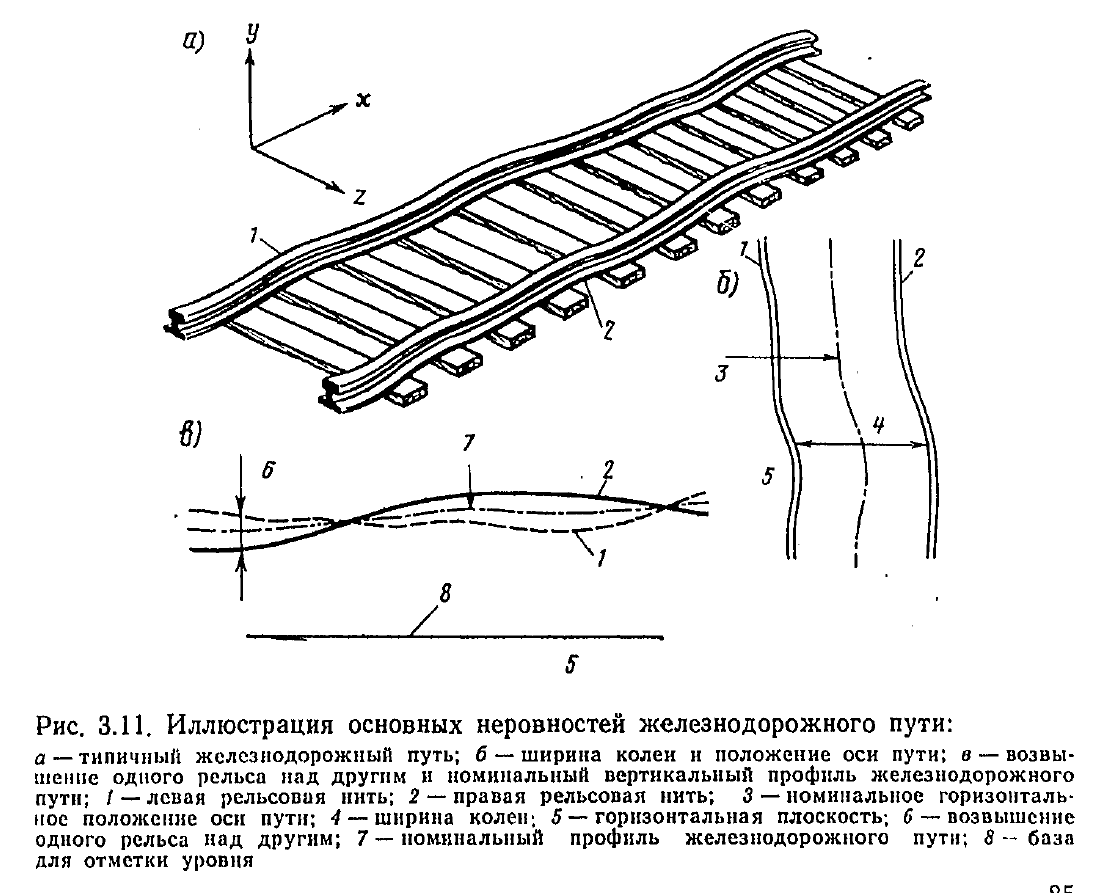
Колебания вагона возникают и из-за неравномерного износа поверхности катания колеса (рис. 5) или эксцентричного его положения на оси (рис. 6). В самом деле, при качении изношенного колеса, имеющего различные радиусы качения в разных точках, центр колеса О будет совершать непрерывные колебания, передаваемые кузову вагона. Совершенно аналогичную картину наблюдают и при движении колеса, установленного на оси с эксцентриситетом е.
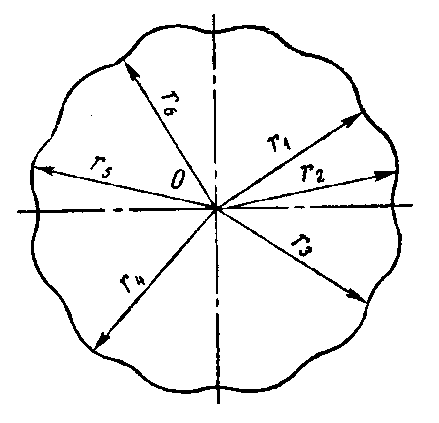 Рис. 5
Рис. 5
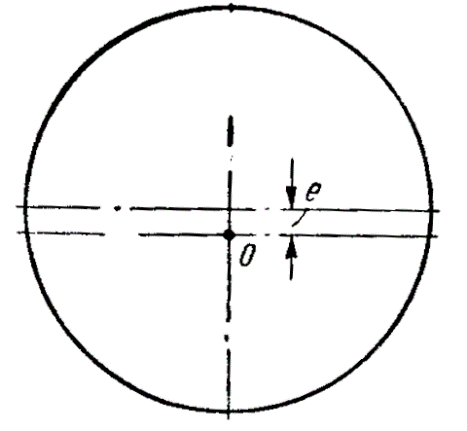 Рис. 6
Рис. 6
Одной из причин колебаний вагона является его виляние (извилистое движение). Как известно, между гребнями колес и рабочими гранями рельсов существуют зазоры, за счет вторых колесная пара при своем движении может постепенно переходить от контактирования гребнем правого колеса с правым по ходу рельсом к контактированию гребнем левого колеса с левым рельсом.
Характеристики колесной пары:
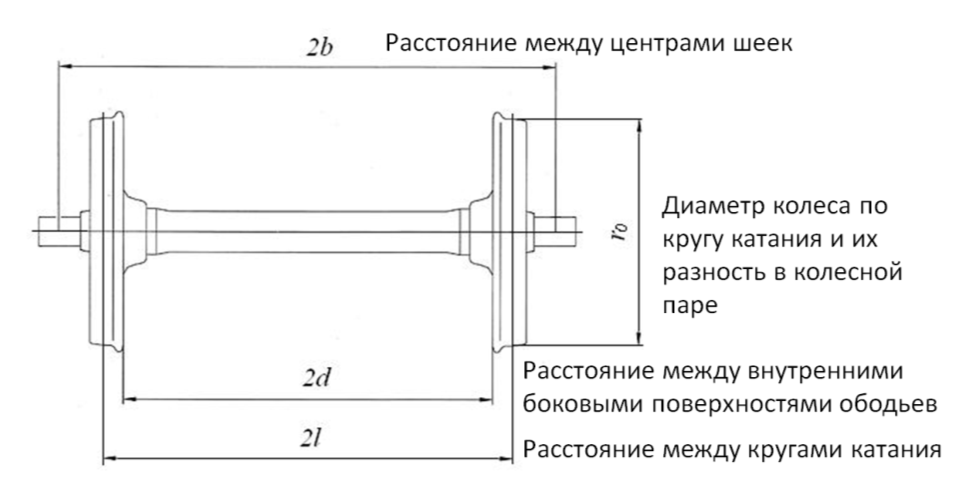
Рис.7
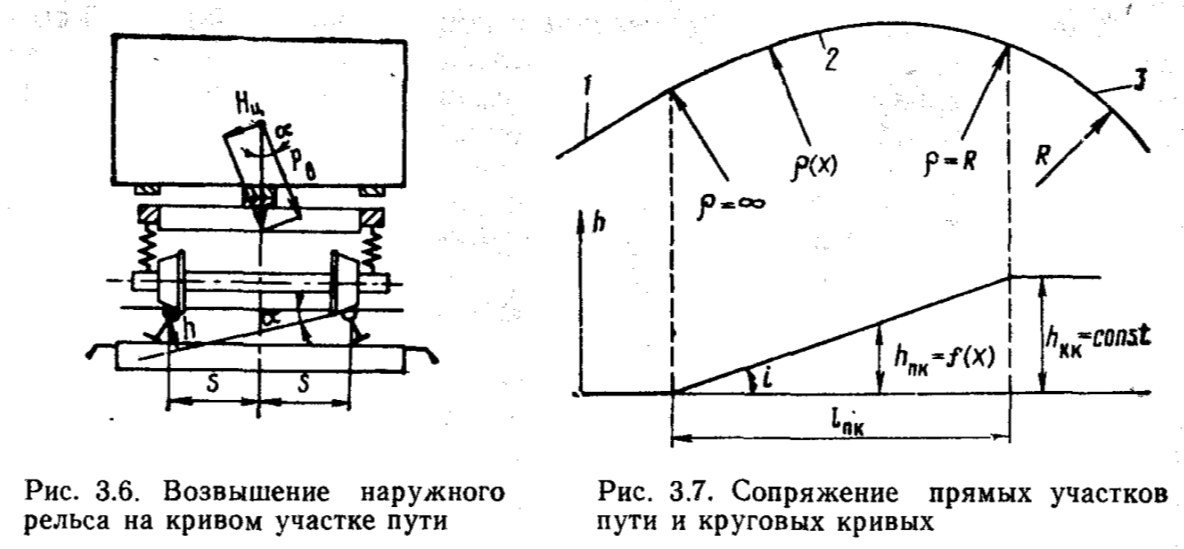
Для обеспечения безопасности движения поездов и снижения сил взаимодействия колеса и рельса относительное расположение рельсов должно отвечать особенностям конструкции ходовых частей подвижного состава. Расположение колесной пары в рельсовой колее показано на рис. 8.
Подуклонка рельсов. Поскольку поверхности катания новых колес имеют уклон 1/20, то и рельсы устанавливаются с наклоном внутрь колеи равным 1/20. Этим достигается большая центрированность опирания бандажа на головку рельса, и за счет этого некоторое снижение напряжений в рельсе и уменьшение пластических деформаций в его головке.

Рис. 8. Схема расположения колесной пары в рельсовой колее
Колесная колея – расстояние между поверхностями гребней колесной пары, измеренное на расстоянии 18 мм от их вершины.
Размеры колесной колеи с учетом допусков на изготовление и износ для колесных пар грузовых/пассажирских вагонов меняются в пределах, указанных в таблице.
Таблица
| Основные размеры, мм | max | min | Номинал |
| Толщина гребня | 33/33 | 25/25 | 33/33 |
| Насадка колес | 1443/1443 | 1437/1439 | 1440 /1440 |
| Колесная колея | 1509/1509 | 1487/1489 | 1506/1506 |
Примечание. Разница в заштрихованных ячейках появляется только для колесных пар, предназначенных для скорости более 33,0 м/с (120 км/ч).
Рельсовая колея – расстояние между головками рельсов, измеренное в плоскости, лежащей па 13 мм ниже плоскости, проходящей через верхнюю точку поверхности катания рельсов. Стандартный размер ширины колеи после сужения, мм – 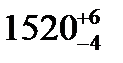 (1516 – 1526), до сужения –
(1516 – 1526), до сужения – 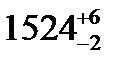 (1522 – 1530).
(1522 – 1530).
В кривых для обеспечения свободного прохода многоосных экипажей ширина колеи больше, чем в прямых (если 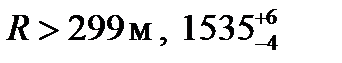 ). Максимальная ширина колеи в кривых – 1541 мм (до сужения было – 1546 мм).
). Максимальная ширина колеи в кривых – 1541 мм (до сужения было – 1546 мм).
Определим величину зазоров между рабочими гранями гребней и боковыми гранями головок рельсов для прямых участков пути.
Минимальный зазор 1516-1509=7 мм (1522-1509=13 мм).
Номинальный зазор 1520-1506=14 мм (1524-1506=18 мм).
Максимальный зазор 1526-1487=39 мм (1526-1487=43 мм).
Вследствие изгиба оси и отжатия головки рельса под действием поперечных сил величина зазора может быть больше приведенных величин. Дополнительное уширение колеи за счет отжатия рельса может достигать 3 – 5 мм. За счет изгиба оси колесной пары зазор между гребнями колес и головками рельсов увеличивается на 1 – 2 мм.
За счет конической поверхности катания при движении по прямой колесная пара описывает синусоиду (извилистое движение). При этом она касается гребнем рельса с одной стороны.
В кривых, очевидно, колесная пара прижимается гребнем к наружному рельсу под действием ускорения. При прижатии гребень трется о рельс.
Поскольку колесная пара при движении непрерывно перемещается поперек колеи (в пределах указанного выше зазора), то ось колесной пары при конической форме колес совершает угловые колебания (см. рис. 4) вокруг оси х (угол j), шейки оси то поднимаются, то опускаются на некоторую величину z. Эти колебания также передаются затем другим элементам вагона.
Колебания вагонов вызываются также действием сил, возникающих при входе вагона в кривые участки пути и в стрелочные кривые, от порывов ветра, аэродинамических толчков воздуха в боковую поверхность вагонов при встрече поездов по некоторым другим причинам.
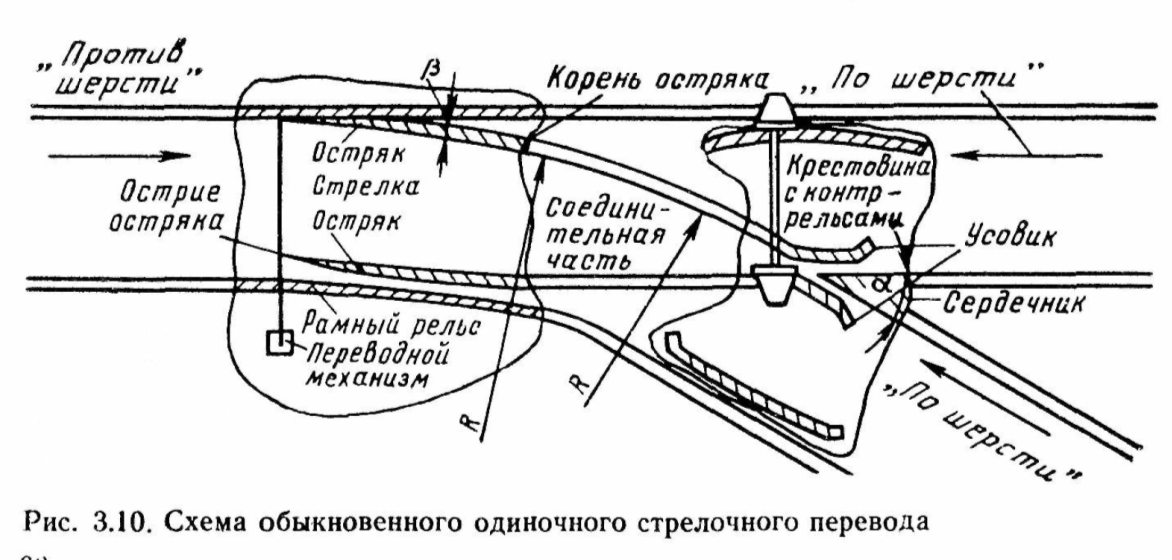
Виды колебаний вагона в заданной системе координат. Основные понятия.
Расчетную схему вагона с двухступенчатым подвешиванием можно представить в виде, показанном на рис.. Колебания кузова по обобщенным координатам – виды колебаний – имеют следующие общепринятые названия:
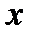 – подергивание – линейные смещения ЦМ кузова вдоль оси
– подергивание – линейные смещения ЦМ кузова вдоль оси 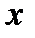 ;
;
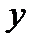 – боковой относ – линейные смещения ЦМ кузова вдоль оси
– боковой относ – линейные смещения ЦМ кузова вдоль оси 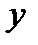 ;
;
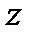 – подпрыгивание – линейные смещения ЦМ кузова вдоль оси
– подпрыгивание – линейные смещения ЦМ кузова вдоль оси 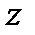 ;
;
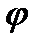 – галопирование – угловые смещения кузова относительно оси
– галопирование – угловые смещения кузова относительно оси 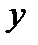 ;
;
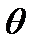 – боковая качка – угловые смещения кузова относительно оси
– боковая качка – угловые смещения кузова относительно оси 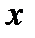 ;
;
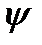 – виляние – угловые смещения кузова относительно оси
– виляние – угловые смещения кузова относительно оси 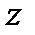 .
.
Без индекса координаты относящиеся к кузову, с индексом 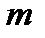 – к тележке и индексом
– к тележке и индексом 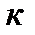 колесной паре.
колесной паре.
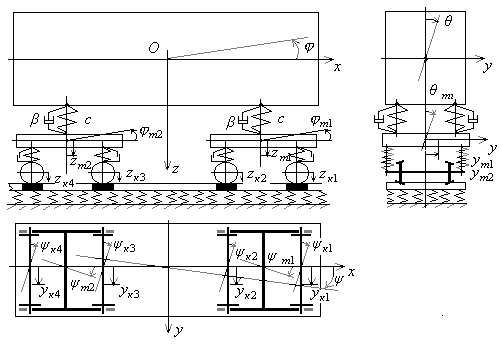
Рис. Расчетная схема вагона с двухступенчатым подвешиванием
Напомним вначале некоторые основные понятия из теории колебаний. В линейных колебательных системах известны два вида колебаний: собственные и вынужденные.
Собственные колебания происходят в изолированных колебательных системах вследствие какого-либо начального возмущения; в процессе самих собственных колебаний никакие внешние дополнительные возмущения на систему не действуют.
Обычно собственные колебания из-за наличия сопротивлений среды с течением времени затухают (прекращаются). Системы, в которых энергия колебаний расходуется на преодоление сопротивлений среды, называют диссипативными, а системы, у которых энергия в окружающую среду не рассеивается — консервативными.
Вынужденные колебания в колебательных системах возникают тогда, когда на систему все время действуют возмущающие силы.
Полнее всего изучены, так называемые, гармонические колебания систем, которые описываются обычно уравнением
z = A sin (vt+a), (1.3)
где z — величина перемещений в колебательном процессе;
A — амплитуда колебаний;'
vt+a — фаза колебаний;
v — угловая частота колебаний;
t — время;
a — начальная фаза колебаний.
Напомним, что периодом колебаний Т (в сек) называют промежуток времени, за который какой-то элемент системы совершает полный цикл колебаний, после которого движение повторяется. Очевидно, это будет тогда, когда фаза колебаний изменяется на 2p, т. е. v(t + T) + a = vt + a + 2p.
Отсюда vТ =2p.
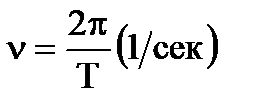 (1.4)
(1.4)
Таким образом, угловой частотой колебаний называется угол (в радианах), на который изменяется фаза за время одного периода. Иногда рассматривают линейную частоту колебаний, т. е. количество периодов колебаний, происходящих в одну секунду, или
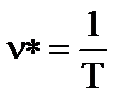 (1.5)
(1.5)
Из формул (1.4) и (1.5) следует, что
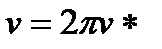 (1.6)
(1.6)
Основные задачи теории колебаний
Дата добавления: 2016-10-26; просмотров: 2984;











