Вынужденные колебания вагона на рессорах с линейными упругими элементами без трения

Рассмотрим вынужденные колебания системы, изображенной на рис. 11. Представим себе, что она изображает движение подвешенной на колесе массы m, когда колесо катится по жесткому пути, имеющему неровности косинусоидальной формы.

В этой системе силы инерции массы т, т. е. 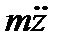, уравновешиваются силами, возникающими при деформации рессоры (z - z_к), т. е. силой с (z - z_к). Следовательно, 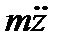+ с (z - z_к) = 0.

Если z_к = h cos w t (см. рис. 11), то

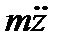+ с z = c h cos w t (1.43)

Поделив все члены этого уравнения на m, получим

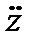+ v² z = v² h cos w t (1.44)

где 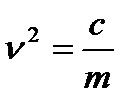— круговая частота свободных колебаний системы (см. § 2).

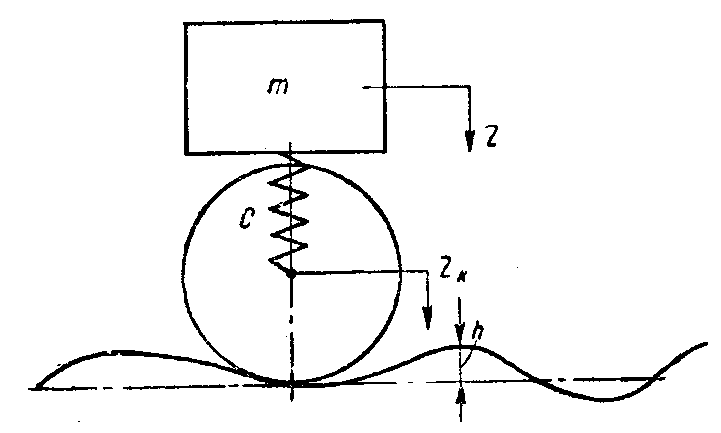
Рис. 11

Общее решение этого уравнения с правой частью (неоднородного) можно представить как сумму решения однородного уравнения z₁ и частного решения неоднородного уравнения z₂, т. е. z = z₁ + z₂.

Найдем вначале частное решение уравнения. Представим, что

z₂ = A₂ cos w t (1.45)

и подставим его в уравнение (1.44). В результате получим

- A₂w² cos w t + v²A₂cos w t = v²h cos w t

Откуда

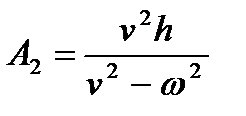, т.е. .

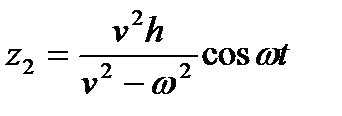Решение однородного уравнения можно, как известно, представить в виде

z₁ = A₁ cos v t

Тогда общее решение уравнения (1.44) представляется как

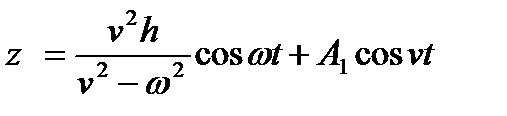. (1.46)

Начало отсчета времени (t =0) в этой системе можно принять для такого момента, когда z =0. В таком случае, подставляя в (1.46) t =0, и z = 0, получим 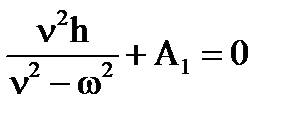. Следовательно 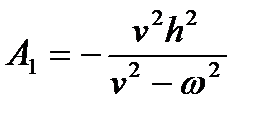. Подставляя A₁ в (1.46), получим

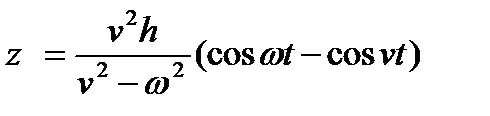(1.47)

Величину 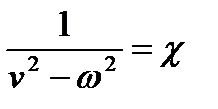называют коэффициентом нарастания колебаний. Приняв это обозначение, уравнение (1.47) запишется

z = c h v² (cos w t - cos v t). (1.48)

Это и будет общим решением нашего уравнения при принятых выше начальных условиях.

Исследуем поведение колебательной системы в том случае, когда частота возмущений ω приближается к частоте собственных колебаний v.

Для удобства дальнейшего анализа формулу (1.47) представим в следующем виде:

.

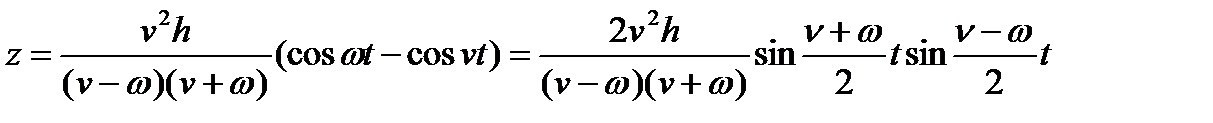Обозначая v - w = 2e, подставим это выражение в предыдущую формулу и, полагая, что v ® w , получим

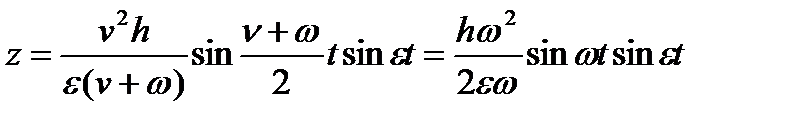
или

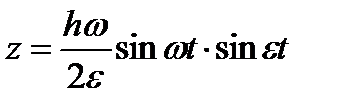. (1.49)

Поскольку e малая величина, то ее период Т₁ весьма велик и значительно больше периода Т₂, определяемого частотой возмущений за счет неровностей w.

Это позволяет рассматривать такие колебания (при близких w и v), как колебания с частотой w и с переменной амплитудой, равной 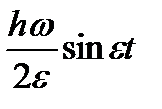. Такие колебания называют биением (рис. 12) с периодом 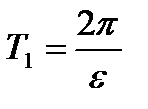. С приближением w к v период Т₁ увеличивается. При точном совпадении величин v и w наступает явление резонанса.

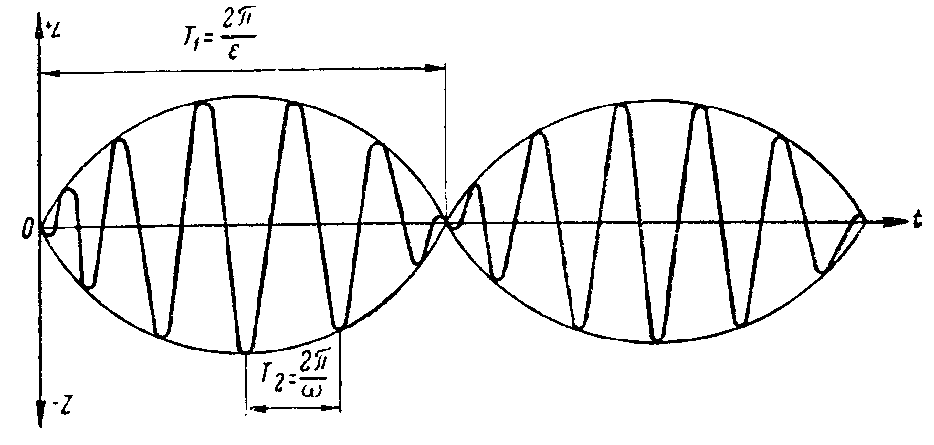
Рис. 12

Когда v станет равным w, можно принять sin et = et. В таком случае

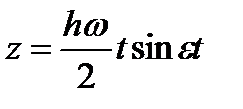(1.50)

График таких колебаний представлен на рис. 13. Он показывает, как развиваются колебания при резонансе. Совершенно очевидно, что при резонансе амплитуда колебаний возрастает прямо пропорционально времени t.

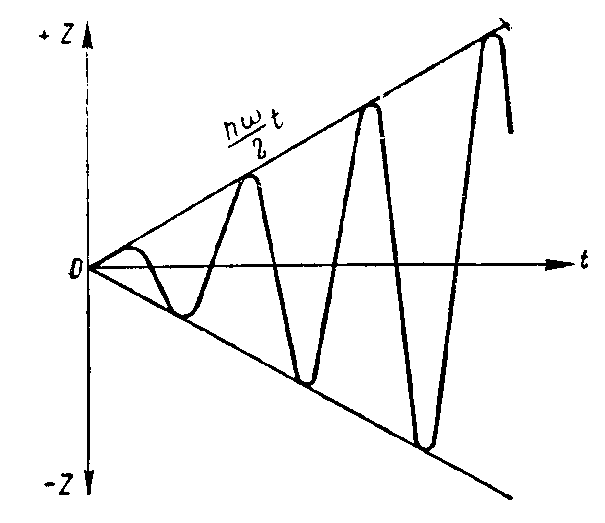
Рис. 13

За каждый период колебаний 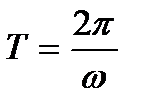амплитуда возрастает на величину

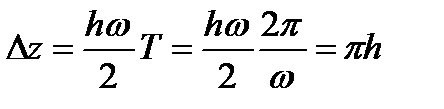(1.51)

Анализ системы с двумя степенями свободы (см. § 2) может быть проведен совершенно аналогично; в этом случае возможны два резонанса при приближении частоты w к частоте l₁ или частоте l₂, т. е. к той или иной собственной частоте.