Метод условной линеаризации
Основная идея метода условной линеаризации состоит в замене нелинейной характеристики отрезком прямой на ее рабочем участке. Рассмотрим применение данного метода на примере.
Пример 15.Найти закон изменение напряжения на конденсаторе при замыкании ключа в цепи на рис.68.а ВАХ диода приведена на рис.68.б.
Решение.Для нахождения рабочих точек на ВАХ диода до замыкания и после замыкания ключа применим метод эквивалентного генератора. Заменим всю цепь, кроме ветви с вентилем (нелинейное сопротивление) активным двухполюсником (рис.69).
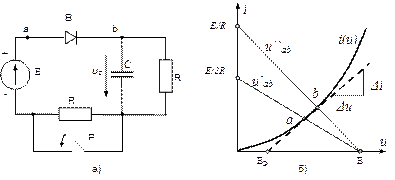
Рис.68. Схема цепи и ВАХ диода
Напряжение uab при разомкнутом ключе:
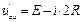 . (94)
. (94)
Конденсатор на установившийся режим при постоянной ЭДС не оказывает влияние. Напряжение Uab при замкнутом ключе:
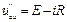 . (95)
. (95)
Получили два уравнения прямой линии. Эти две прямые построены на рис.68.б.
 При
При 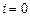
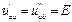 .
.
При 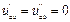 :
:
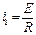 ,
, 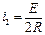 . (96)
. (96)
Точки пересечения этих прямых с ВАХ диода дают установившиеся значения напряжения и тока до и после замыкания ключа, т.е. определяют предельные значения напряжения на диоде. Проведя прямую через эти точки a и b, мы условно линеаризируем ВАХ в рабочей зоне. Уравнение прямой:
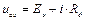 , (97)
, (97)
где 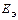 ,
, 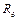 - параметры схемы замещения диода.
- параметры схемы замещения диода.
Рис.69. Эквивалентный двухполюсник
Дифференциальное сопротивление диода 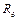 - определяют из ВАХ:
- определяют из ВАХ:
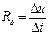 . (98)
. (98)
Диод замещают источником ЭДС 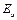 , включенной последовательно с линейным сопротивлением
, включенной последовательно с линейным сопротивлением 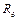 . (рис.70)
. (рис.70)
 В итоге исходную нелинейную цепь можно представить в виде линейной цепи, для которой переходная функция напряжения конденсатора определяется уравнением:
В итоге исходную нелинейную цепь можно представить в виде линейной цепи, для которой переходная функция напряжения конденсатора определяется уравнением:
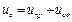 . (99)
. (99)
Рис.70. Схема замещения диода
Эквивалентная схема всей цепи представлена на рис.71.

Для схемы замещения:
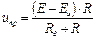 , (101)
, (101)
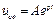 , (102)
, (102)
где А – постоянная интегрирования;
p – корень характеристического уравнения.
Переходная функция напряжения на конденсаторе:
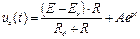 . (103)
. (103)
Рис.71. Эквивалентная цепь
Составим характеристическое уравнение для эквивалентной цепи:
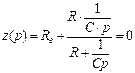 , (104)
, (104)
откуда: 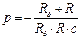 . (105)
. (105)
Определим постоянную интегрирования из начальных условий. При 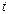 =0, напряжение на конденсаторе:
=0, напряжение на конденсаторе:
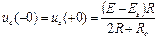 . (106)
. (106)
Подставляя значение для переходной функции (100), получим:
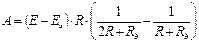 . (107)
. (107)
В итоге переходная функция напряжения на конденсаторе:
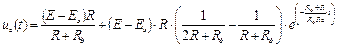 . (108)
. (108)
Дата добавления: 2016-10-26; просмотров: 2330;











