Опасности общего модуля

Хотя DSS не определяет применение пользователями общего модуля, различные реализации могут воспользоваться такой возможностью. Íàïðèìåð, Налоговое управление рассматривает использование DSS для электронной налогов. Что если эта организация потребует, чтобы все налогоплательщики страны использовали общие pи q? Общий модуль слишком легко становится мишенью для криптоанализа. Пока слишком рано обсуждать различные реализации DSS, но причины для беспокойства есть.

Подсознательный канал в DSA

Гус Симмонс (Gus Simmons) открыл в DSA подсознательный канал [1468, 1469] (см. раздел 23.3). Этот подсознательный канал позволяет встраивать в подпись тайное сообщение, которое может быть прочитано только тем, у кого есть ключ. Согласно Симмонсу, это "замечательное совпадение", что "все очевидные недостатки подсознательных каналов, использующих схему ElGamal, могут быть устранены" в DSS, и что DSS "на сегодня обеспечивает наиболее подходящую среду для подсознательных коммуникаций". NIST и NSA не комментировали этот подсознательный канал, никто даже не знает, догадывались ли они о такой возможности. Так как этот подсознательный канал позволяет при недобросовестной реализации DSS передавать с каждой подписью часть закрытого ключа. Никогда на пользуйтесь реализацией DSS, если вы не доверяете разработчику реализации.

Патенты

Дэвид Кравиц (David Kravitz), ранее работавший в NSA, владеет патентом DSA [897]. Согласно NIST [538]:

NIST в интересах общества стремится сделать технологию DSS доступной бесплатно по всему миру. Мы считаем, что эта технология может быть запатентована, и что никакие другие патенты не применимы к DSS, но мы не можем дать твердых гарантий этого до получения патента.

Несмотря на это, три владельца патентов утверждают, что DSA нарушает их патенты: Diffie-Hellman (см. раздел 2.2.1) [718], Merkle-Hellman (см. раздел 19.2.) [720] и Schnorr (см. раздел 21.3) [1398]. Патент Schnorr является источником наибольших сложностей. Срок действия двух других патентов истекает 1997 году, а патент Schnorr действителен до 2008 года. Алгоритм Schnorr был разработан не на правительственные деньги. В отличие от патентов PKP у правительства США нет прав на патент Schnorr, и Шнорр запатентовал свой алгоритм по всему миру. Даже если суды США вынесут решение в пользу DSA, неясно, какое решение примут суды в других странах. Сможет ли международная корпорация принять стандарт, который законен в одних странах и нарушает патентное законодательство в других? Нужно время, чтобы решить эту проблему, к моменту написания этой книги этот вопрос не решен даже в Соединенных Штатах.

В июне 1993 года NIST предложил выдать PKP исключительную патентную лицензию на DSA [541]. Соглашение провалилось после протестов общественности и стандарт вышел в свет без всяких соглашений. NIST заявил [542]:

 . . NIST рассмотрел заявления о возможном нарушении патентов и сделал вывод, что эти заявления несправедливы.

Итак стандарт официально принят, в воздухе пахнет судебными процессами, и никто не знает, что делать. NIST заявил, что он поможет защититься людям, обвиненным в нарушении патентного законодательства при использовании DSA в работе по правительственному контракту. Остальные, по видимому, должны заботиться о себе сами. Проект банковского стандарта, использующего DSA, выдвинут ANSI [60]. NIST работает над введением стандарта DSA в правительственном аппарате. Shell Oil сделала DSA своим международным стандартом. О других предложенных стандартах DSA мне неизвестно.

Варианты DSA

Этот вариант делает проще вычисления, необходимые для подписи, не заставляя вычислять k^-1 [1135]. Все используемые параметры - такие же, как в DSA. Для подписи сообщения m Àëèñà генерирует два случайных числа, kи d, меньшие q. Процедура подписи выглядит так

r= (g^k mod p)mod q

s = (H(m)+ xr) * dmod q

t = kd mod q

Áîá проверяет подпись, вычисляя

w = t/s mod q

u₁ = (H(m) * w)mod q

u₂ = (rw)mod q

Если r = (( 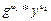) mod p) mod q, то подпись правильна.

Следующий вариант упрощает вычисления при проверке подписи [1040, 1629]. Все используемые параметры - такие же, как в DSA. Для подписи сообщения m Àëèñà генерирует случайное число k, меньшее q. Процедура подписи выглядит так

r= (g^k mod p)mod q

s = k (H(m)+ xr)^-1mod q

Áîá проверяет подпись, вычисляя

u₁ = (H(m) *s)mod q

u₂ = (sr)mod q

Если r = (( 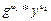) mod p) mod q, то подпись правильна.

Еще один вариант DSA разрешает пакетную проверку, Áîá может проверять подписи пакетами [1135]. Если все подписи правильны, то работа Боба закончена. Если одна из них неправильна, то ему еще нужно понять, какая. К несчастью, это небезопасно. Либо подписывающий, либо проверяющий может легко создать набор фальшивых подписей, который удовлетворяет критерию проверки пакета подписей [974].

Существует также вариант генерации простых чисел для DSA, который включает qи используемые для генерации простых чисел параметры внутрь p. Влияет ли эта схема на безопасность DSA, все еще неизвестно.

(1) Выберем произвольную последовательность, по крайней мере, 160 битов и назовем ее S. Пусть g- это длина Sв битах.

(2) Вычислим U= SHA(S)Å SHA((S + 1) mod 2^g), где SHA описан в разделе 18.7.

(3) Образуем q, установив наибольший и наименьший значащие биты Uв 1.

(4) Проверим, является ли q простым.

(5) Пусть p- это объединение q, S, C и SHA(S ). Cпредставляет собой 32 нулевых бита.

(6) p=p-(pmodq)+l.

(7) p=p+q.

(8) Если Cв pравно 0x7fffffff, вернемся на этап (1).

(9) Проверим, является ли p простым.

(10) Если p - составное, вернемся на этап (7).

Преимуществом этого варианта является то, что вам не нужно хранить значения C и S, использованные для генерации pи q. Они включены в состав p. Для приложений, работающих в условиях нехватки памяти, например, для интеллектуальных карточек, это может быть важно.