Схемы цифровой подписи с использованием дискретных логарифмов
Схемы подписи ElGamal, Schnorr (см. раздел 21.3) и DSA очень похожи. По сути, все они являются тремя примерами общей схемы цифровой подписи, использующей проблему дискретных логарифмов. Вместе с тысячами других схем подписей они являются частью одного и того же семейства [740, 741, 699, 1184].
Выберем p, большое простое число, и q, равное либо p-1, либо большому простому множителю p-1. Затем выберем g, число между 1 и p, для которого gqº 1 (mod p). Все эти числа открыты, и могут быть совместно использованы группой пользователей. Закрытым ключом является x, меньшее q. Открытым ключом служит y=gx mod q.
Чтобы подписать сообщение m, сначала выберем случайное значение k, меньшее q и взаимно простое с ним. Если qтоже простое число, то будет работать любое k, меньшее q. Сначала вычислим
r= gk mod p
Обобщенное уравнение подписи примет вид
ak= b+ cxmod q
Коэффициенты a, b и c могут принимать различные значения. Каждая строка Табл. 20-4 предоставляет шесть возможностей. Проверяя подпись, получатель должен убедиться, что
ra= gbyc mod p
Это уравнение называется уравнением проверки.
Табл. 20-4.
Возможные перестановки a, b и c (r'= r mod q)
| ± r' | ± s | m |
| ± r' m | ± s | |
| ± r' m | ± ms | |
| ± m r' | ± r' s | |
| ± ms | ± r' s |
В Табл. 20-5 перечислены возможные варианты подписи и проверки, полученные только из первой строки возможных значений a, b и c без учета эффектов ±.
Табл. 20-5.
Схемы цифровой подписи с использованием дискретных логарифмов
| Уравнение подписи | Уравнение проверки |
| (1) r'k=s+mx modq | rr'=gsym mod p |
| (2) r'k=m+sx modq | rr'=gmys mod p |
| (3) sk= r'+mx modq | rs=gr'ym mod p |
| (4) sk= m+ r'x modq | rs=gmyr' mod p |
| (5) mk= s+ r'x modq | rm=gsyr' mod p |
| (6) mk= r'+sx modq | rm=gr'ys mod p |
Это шесть различных схем цифровых подписей. Добавление минуса увеличивает их количество до 24. При использовании всех возможных значения a, b и c число схем доходит 120.
EIGamal [518, 519] и DSA [1154] по существу основаны на уравнении (4). Другие схемы - на уравнении (2) [24, 1629]. Schnorr [1396, 1397], как и другая схема [1183], тесно связан с уравнением (5). А уравнение (1) можно изменить так, чтобы получить схему, предложенную в [1630]. Оставшиеся уравнения - новые.
Далее. Любую из этих схем можно сделать более DSA-подобной, определив r как
r= (gk mod p)mod q
Используйте то же уравнение подписи и сделайте уравнением проверки
u1 = a-1bmod q
u2 = a-1cmod q
v= (( 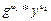 ) mod p) mod q
) mod p) mod q
(r mod q)a = gbycmod p
Существуют и две другие возможности подобных преобразований [740, 741]. Такие операции можно проделать с каждой из 120 схем, доведя общее число схем цифровой подписи, использующих дискретные логарифмы, до 480.
Но и это еще не все. Дополнительные обобщения и изменения приводят более, чем к 13000 вариантам (не все из них достаточно эффективны) [740, 741].
Одной из приятных сторон использования RSA для цифровой подписи является свойство, называемое восстановлением сообщения. Когда вы проверяете подпись RSA, вы вычисляете m. Затем вычисленное mсравнивается с сообщением и проверяется, правильна ли подпись сообщения. В предыдущих схемах восстановить m при вычислении подписи невозможно, вам потребуется вероятное m, которое и используется в уравнении проверки. Но, оказывается, можно построить вариант с восстановлением сообщения для всех вышеприведенных схем. Для подписи сначала вычислим
r= mgk mod p
и заменим mединицейв уравнении подписи. Затем можно восстановит уравнение проверки так, чтобы mмогло быть вычислено непосредственно. То же самое можно предпринять для DSA-подобных схем:
r= (mgk mod p) mod q
Безопасность всех вариантов одинакова, поэтому имеет смысл выбирать схему по сложности вычисления. Большинство схем замедляет необходимость вычислять обратные значения. Как оказывается, одна из этих схем позволяет вычислять и уравнение подписи, и уравнение проверки без использования обратных значений, при этом еще и восстанавливая сообщение. Она называется схемой p-NEW [1184].
r= mg-k mod p
s= k- r'x mod q
mвосстанавливается (и проверяется подпись) с помощью вычисления
m= gsyr'rmod p
В ряде вариантов одновременно подписывается по два-три блока сообщения [740], другие варианты можно использовать для слепых подписей [741].
Это значительная область для изучения. Все различные схемы цифровой подписи с использованием дискретных логарифмов были объединены логическим каркасом. Лично я считаю, что это окончательно положит конец спорам между Schnorr [1398] и DSA [897]: DSA не является ни производной Schnorr, равно как и EIGamal. Все три алгоритма являются частными случаями описанной общей схемы, и эта общая схема незапатентована.
ONG-SCHNORR-SHAMIR
Эта схема подписи использует многочлены по модулю n [1219, 1220]. Выбирается большое целое число (знать разложение nна множители не обязательно). Затем выбирается случайное число k, взаимно простое с n, и вычисляется h, равное
h = -k-2 mod n= -(k-1)2 mod n
Открытым ключом служат hи n; а закрытым - k.
Чтобы подписать сообщение M, сначала генерируется случайное число r, взаимно простое с n. Затем вычисляется:
S1= 1/2 (M/r+r) mod n
S2= 1/2 (M/r-r) mod n
Пара чисел S1 и S2 представляет собой подпись. Проверяя подпись, убеждаются, что
S12 + h*S22º M (mod n)
Описанный здесь вариант схемы основан на квадратичных многочленах. При его опубликовании в [1217] за успешный криптоанализ было предложено вознаграждение в $100. Небезопасность схемы была доказана [1255, 18], но это не остановило ее авторов. Они предложили модификацию алгоритма, основанную на кубических многочленах, также оказавшуюся небезопасной [1255]. Авторы предложили версию на базе многочленов четвертой степени, но была взломана и она [524, 1255]. Вариант, решающий эти проблемы, описан в [1134].
ESIGN
ESICN -это схема цифровой подписи, разработанная NTT Japan [1205, 583]. Утверждалось, что она не менее безопасна, чем RSA или DSA, и намного быстрее при тех же размерах ключа и подписи. Закрытым ключом служит пара больших простых чисел pи q. Открытым ключом является n, для которого
n = p2*q
H- это хэш-функция, применяемая к сообщению m, причем значение H(m) находится в пределах от 0 до n-1. Используется также параметр безопасности k, который будет вкратце рассмотрен.
(1) Àëèñà выбирает случайное число x, меньшее pq.
(2) Àëèñà вычисляет:
w, наименьшее целое, которое больше или равно
(H(m) - xkmod n)/pq
s= x+ ((w/kxk-1 mod p) pq
(3) Àëèñà посылает s Áîáу.
(4) Для проверки подписи Áîá вычисляет skmod n. Кроме этого, он вычисляет a, наименьшее целое, которое больше или равно удвоенному числу битов n, деленному на 3. Если H(m) меньше или равна skmod n, и если skmod n меньше H(m)+2a, то подпись считается правильной.
Выполнив ряд предварительных вычислений, этот алгоритм можно ускорить. Эти вычисления могут быть выполнены в произвольный момент времени и никак не связаны с подписываемым сообщением. Выбрав x, Àëèñà может разбить этап (2) на два подэтапа. Сначала.
(2a) Àëèñà вычисляет:
u= xkmod n
v = l/(kxk-1) mod p
(2b) Àëèñà вычисляет:
w= наименьшее целое, которое больше или равно
(H(m) - u)/pq
s= x+ ((wv mod p) pq
Для обычно используемых размеров чисел предварительные вычисления ускоряют процесс подписи на порядок. Почти вся трудная работа выполняется именно на стадии предварительных вычислений. Обсуждение действий модульной арифметики, выполняемых при ускорении ESIGN, можно найти в [1625, 1624]. Этот алгоритм можно расширить для работы с эллиптическими кривыми [1206].
Безопасность ESIGN
Когда этот алгоритм был впервые предложен, kбыло выбрано равным 2 [1215]. Такая схема быстро была взломана Эрни Брикеллом (Ernie Brickell) и Джоном ДеЛаурентисом [261], которые распространили свое вскрытие и на случай k= 3. Модифицированная версия этого алгоритма [1203] была взломана Шамиром [1204]. Вариант, предложенный в [1204], был взломан в [1553]. ESIGN - это сегодняшняя реинкарнация алгоритмов из этого семейства. Попытка вскрыть ESIGN [963] оказалась безрезультатной.
В настоящее время авторы рекомендуют использовать следующие значения k: 8, 16, 32, 64, 128, 256, 512 и 1024. Они также рекомендуют, чтобы pи qбыли не меньше 192 битов каждое, образуя n не менее, чем 576 битов в длину. (Я думаю, что n должно быть еще в два раза больше.) Авторы считают, что с такими значениями параметров, безопасность ESIGN равна безопасности RSA или Rabin. И выполненный ими анализ показывает, что скорость ESIGN намного выше, чем у RSA, EIGamal и DSA [582].
Патенты
ESICN запатентован в Соединенных Штатах [1208], Канаде, Англии, Франции, Германии и Италии. Любой, кто хочет получить лицензию на алгоритм, должен обратиться в Отдел интеллектуальной собственности NTT (Intellectual Property Department, NTT, 1-6Uchisaiwai-cho, 1-chome, Chiyada-ku, 100 Japan).
Клеточные автоматы
Совершенно новая идея, изученная Папуа Гуамом (Papua Guam) [665], состоит в использовании в криптосистемах с открытыми ключами клеточных автоматов. Эта система все еще слишком нова и не прошла через тщательное изучение, но предварительное исследование показало, что у нее может быть такое же криптографически слабое место, как и у других систем [562]. Тем не менее, это многообещающая область исследований. Свойством клеточных автоматов является то, что даже если они инвертируемы, невозможно вычислить предка произвольного состояния, инвертировав правило нахождения потомка. Это выглядит очень похоже на однонаправленную хэш-функцию с лазейкой.
Дата добавления: 2021-01-26; просмотров: 512;











